Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T14:52:03.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Recovery of wall-shear stress to equilibrium flow conditions after a rough-to-smooth step change in turbulent boundary layers

Published online by Cambridge University Press:  10 June 2019

Mogeng Li Open the ORCID record for Mogeng Li [Opens in a new window] ,
Charitha M. de Silva Open the ORCID record for Charitha M. de Silva [Opens in a new window] ,
Amirreza Rouhi Open the ORCID record for Amirreza Rouhi [Opens in a new window] ,
Rio Baidya Open the ORCID record for Rio Baidya [Opens in a new window] ,
Daniel Chung Open the ORCID record for Daniel Chung [Opens in a new window] ,
Ivan Marusic  and
Nicholas Hutchins
Mogeng Li*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Charitha M. de Silva
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Amirreza Rouhi
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Rio Baidya
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Daniel Chung
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Nicholas Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper examines the recovery of the wall-shear stress of a turbulent boundary layer that has undergone a sudden transition from a rough to a smooth surface. Early work of Antonia & Luxton (J. Fluid Mech., vol. 53, 1972, pp. 737–757) questioned the reliability of standard smooth-wall methods for measuring wall-shear stress in such conditions, and subsequent studies show significant disagreement depending on the approach used to determine the wall-shear stress downstream. Here we address this by utilising a collection of experimental databases at 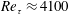$Re_{\unicode[STIX]{x1D70F}}\approx 4100$ that have access to both ‘direct’ and ‘indirect’ measures of the wall-shear stress to understand the recovery to equilibrium conditions of the new surface. Our results reveal that the viscous region (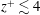$z^{+}\lesssim 4$) recovers almost immediately to an equilibrium state with the new wall conditions; however, the buffer region and beyond takes several boundary layer thicknesses before recovering to equilibrium conditions, which is longer than previously thought. A unique direct numerical simulation database of a wall-bounded flow with a rough-to-smooth wall transition is employed to confirm these findings. In doing so, we present evidence that any estimate of the wall-shear stress from the mean velocity profile in the buffer region or further away from the wall tends to underestimate its magnitude in the near vicinity of the rough-to-smooth transition, and this is likely to be partly responsible for the large scatter of recovery lengths to equilibrium conditions reported in the literature. Our results also reveal that smaller energetic scales in the near-wall region recover to an equilibrium state associated with the new wall conditions within one boundary layer thickness downstream of the transition, while larger energetic scales exhibit an over-energised state for several boundary layer thicknesses downstream of the transition. Based on these observations, an alternative approach to estimating the wall-shear stress from the premultiplied energy spectrum is proposed.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 472 - 491
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J Fluid Mech. 500, 135–144.Google Scholar
Antonia, R. A. & Luxton, R. E. 1972 The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough-to-smooth. J. Fluid Mech. 53, 737–757.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2004 Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: blending height and effective surface roughness. Water Resour. Res. 40, W02505.Google Scholar
Bradley, E. F. 1968 A micrometeorological study of velocity profiles and surface drag in the region modified by a change in surface roughness. Q. J. R. Meteorol. Soc. 94, 361–379.Google Scholar
Chamorro, L. P. & Porté-Agel, F. 2009 Velocity and surface shear stress distributions behind a rough-to-smooth surface transition: a simple new model. Boundary-Layer Meteorol. 130, 29–41.Google Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.Google Scholar
Chin, C., Hutchins, N., Ooi, A. & Marusic, I. 2011 Spatial resolution correction for hot-wire anemometry in wall turbulence. Exp. Fluids 50, 1443–1453.Google Scholar
Chung, D., Chan, L., MacDonald, M., Hutchins, N. & Ooi, A. 2015 A fast direct numerical simulation method for characterising hydraulic roughness. J. Fluid Mech. 773, 418–431.Google Scholar
Chung, D., Monty, J. P. & Ooi, A. 2014 An idealised assessment of Townsend’s outer-layer similarity hypothesis for wall turbulence. J. Fluid Mech. 742, R3.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21, 91–108.Google Scholar
Cowen, E. A. & Monismith, S. G. 1997 A hybrid digital particle tracking velocimetry technique. Exp. Fluids 22, 199–211.Google Scholar
Efros, V. & Krogstad, P. A. 2011 Development of a turbulent boundary layer after a step from smooth to rough surface. Exp. Fluids 51, 1563–1575.Google Scholar
Elliott, W. P. 1958 The growth of the atmospheric internal boundary layer. Trans. Am. Geophys. Union 39, 1048–1054.Google Scholar
Fernholz, H. H., Janke, G., Schober, M., Wagner, P. M. & Warnack, D. 1996 New developments and applications of skin-friction measuring techniques. Meas. Sci. Technol. 7, 1396–1409.Google Scholar
Ganapathisubramani, B. 2018 Law of the wall for small-scale streamwise turbulence intensity in high-Reynolds-number turbulent boundary layers. Phys. Rev. Fluids 3, 104607.Google Scholar
Garratt, J. R. 1990 The internal boundary layer – a review. Boundary-Layer Meteorol. 50, 171–203.Google Scholar
Hanson, R. E. & Ganapathisubramani, B. 2016 Development of turbulent boundary layers past a step change in wall roughness. J. Fluid Mech. 795, 494–523.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J Fluid Mech. 715, 477–498.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J Fluid Mech. 635, 103–136.Google Scholar
Ismail, U., Zaki, T. A. & Durbin, P. A. 2018a The effect of cube-roughened walls on the response of rough-to-smooth (RTS) turbulent channel flows. Intl J. Heat Fluid Flow 72, 174–185.Google Scholar
Ismail, U., Zaki, T. A. & Durbin, P. A. 2018b Simulations of rib-roughened rough-to-smooth turbulent channel flows. J. Fluid Mech. 843, 419–449.Google Scholar
Kevin, Nugroho, B., Monty, J. P., Hutchins, N., Pathikonda, G., Barros, J. M. & Christensen, K. T. 2015 Dissecting a modified turbulent boundary layer using particle image velocimetry. In 7th Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion, Melbourne, Australia. Monash University.Google Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mogeng, M. L., de Silva, C. M., Baidya, R., Rouhi, A., Chung, D., Marusic, I. & Hutchins, N. 2018 Recovery of a turbulent boundary layer following a rough-to-smooth step-change in the wall condition. In Proc. 21st Australasian Fluid Mechanics Conference. Australasian Fluid Mechanics Society.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Musker, A. J. 1979 Explicit expression for the smooth wall velocity distribution in a turbulent boundary layer. AIAA J. 17, 655–657.Google Scholar
Ng, H. C. H., Marusic, I., Monty, J. P., Hutchins, N. & Chong, M. S. 2007 Oil film interferometry in high Reynolds number turbulent boundary layers. In Proc. 16th Australasian Fluid Mechanics Conference, Gold Coast, Australia. Australasian Fluid Mechanics Society.Google Scholar
Nugroho, B.2015 Highly ordered surface roughness effects on turbulent boundary layers. PhD thesis, University of Melbourne.Google Scholar
Nugroho, B., Hutchins, N. & Monty, J. P. 2013 Large-scale spanwise periodicity in a turbulent boundary layer induced by highly ordered and directional surface roughness. Intl J. Heat Fluid Flow 41, 90–102.Google Scholar
Patel, V. C. 1965 Calibration of the Preston tube and limitations on its use in pressure gradients. J. Fluid Mech. 23, 185–208.Google Scholar
Rao, K. S., Wyngaard, J. C. & Coté, O. R. 1974 The structure of the two-dimensional internal boundary layer over a sudden change of surface roughness. J. Atmos. Sci. 31, 738–746.Google Scholar
Rouhi, A., Chung, D. & Hutchins, N. 2019 Direct numerical simulation of open channel flow over smooth-to-rough and rough-to-smooth step changes. J. Fluid Mech. 866, 450–486.Google Scholar
Saito, N. & Pullin, D. I. 2014 Large eddy simulation of smooth–rough–smooth transitions in turbulent channel flows. Intl J. Heat Mass Transfer 78, 707–720.Google Scholar
Savelyev, S. A. & Taylor, P. A. 2005 Internal boundary layers: I. Height formulae for neutral and diabatic flows. Boundary-Layer Meteorol. 115, 1–25.Google Scholar
Scotti, A. 2006 Direct numerical simulation of turbulent channel flows with boundary roughened with virtual sandpaper. Phys. Fluids 18, 031701.Google Scholar
Shir, C. C. 1972 A numerical computation of air flow over a sudden change of surface roughness. J. Atmos. Sci. 29, 304–310.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ = 2000. Phys. Fluids 25, 105102.Google Scholar
de Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014 High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26, 025117.Google Scholar
Silva Lopes, A., Palma, J. M. L. M. & Piomelli, U. 2015 On the determination of effective aerodynamic roughness of surfaces with vegetation patches. Boundary-Layer Meteorol. 156, 113–130.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Squire, D. T., Hutchins, N., Morrill-Winter, C., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2017 Applicability of Taylor’s hypothesis in rough- and smooth-wall boundary layers. J. Fluid Mech. 812, 398–417.Google Scholar
Talluru, K. M., Kulandaivelu, V., Hutchins, N. & Marusic, I. 2014 A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas. Sci. Technol. 25, 105304.Google Scholar
Wu, Y., Ren, H. & Tang, H. 2013 Turbulent flow over a rough backward-facing step. Intl J. Heat Fluid Flow 44, 155–169.Google Scholar
Yavuzkurt, S. 1984 A guide to uncertainty analysis of hot-wire data. Trans. ASME 106, 181–186.Google Scholar
Zanoun, E. S., Durst, F. & Nagib, H. 2003 Evaluating the law of the wall in two-dimensional fully developed turbulent channel flows. Phys. Fluids 15, 3079–3089.Google Scholar