Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-29T20:21:14.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Reconsideration of spanwise rotating turbulent channel flows via resolvent analysis

Published online by Cambridge University Press:  19 December 2018

Satoshi Nakashima ,
Mitul Luhar Open the ORCID record for Mitul Luhar [Opens in a new window]  and
Koji Fukagata Open the ORCID record for Koji Fukagata [Opens in a new window]
Satoshi Nakashima
Affiliation:
Department of Mechanical Engineering, Keio University, Yokohama 223-8522, Japan
Mitul Luhar
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Koji Fukagata*
Affiliation:
Department of Mechanical Engineering, Keio University, Yokohama 223-8522, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the effect of spanwise rotation in turbulent channel flow at both low and high Reynolds numbers by employing the resolvent formulation proposed by McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382). Under this formulation, the nonlinear terms in the Navier–Stokes equations are regarded as a forcing that acts upon the remaining linear dynamics to generate the turbulent velocity field in response. A gain-based decomposition of the forcing–response transfer function across spectral space yields models for highly amplified flow structures, or modes. Unlike linear stability analysis, this enables targeted analyses of the effects of rotation on high-gain modes that serve as useful low-order models for dynamically important coherent structures in wall-bounded turbulent flows. The present study examines a wide range of rotation rates. A posteriori comparisons at low Reynolds number (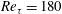$\mathit{Re}_{\unicode[STIX]{x1D70F}}=180$) demonstrate that the resolvent formulation is able to quantitatively predict the effect of varying spanwise rotation rates on specific classes of flow structure (e.g. the near-wall cycle) as well as energy amplification across spectral space. For fixed inner-normalized rotation number, the effects of rotation at varying friction Reynolds numbers appear to be similar across spectral space, when scaled in outer units. We also consider the effects of rotation on modes with varying speed (i.e. modes that are localized in regions of varying mean shear), and provide suggestions for modelling the nonlinear forcing term.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 200 - 222
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brethouwer, G. 2005 The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulations. J. Fluid Mech. 542, 305–342.Google Scholar
Brethouwer, G. 2017 Statistics and structure of spanwise rotating turbulent channel flow at moderate Reynolds number. J. Fluid Mech. 828, 424–458.Google Scholar
Gomez, F., Blackburn, H. M., Rudman, M., Sharma, A. S. & McKeon, B. J. 2016a Streamwise-varying steady transpiration control in turbulent pipe flow. J. Fluid Mech. 796, 588–616.Google Scholar
Gomez, F., Blackburn, H. M., Rudman, M., Sharma, A. S. & McKeon, B. J. 2016b On the coupling of direct numerical simulation and resolvent analysis. In Progress in Turbulence VI, Springer Proceedings in Physics, vol. 165, pp. 87–91. Springer.Google Scholar
Grundestam, O., Wallin, S. & Johansson, A. V. 2008 Direct numerical simulations of rotating turbulent channel flow. J. Fluid Mech. 598, 177–199.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Johnston, J. P., Halleen, R. M. & Lezius, D. K. 1972 Effect of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–557.Google Scholar
Kristoffersen, R. & Andersson, H. I. 1993 Direct simulations of low-Reynolds-number turbulent flow in a rotating channel. J. Fluid Mech. 256, 395–415.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 245–258.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2014 Opposition control within the resolvent analysis framework. J. Fluid Mech. 749, 597–626.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2015 A framework for studying the effect of compliant surfaces on wall turbulence. J. Fluid Mech. 768, 415–441.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2016 On the design of optimal compliant walls for turbulence control. J. Turbul. 17, 787–806.Google Scholar
McKeon, B. J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1.Google Scholar
McKeon, B. J., Jacobi, I. & Sharma, A. S. 2013 Experimental manipulation of wall turbulence: a systems approach. Phys. Fluids 25, 031301.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Moarref, R., Jovanovic, M. R., Sharma, A. S., Tropp, J. A. & McKeon, B. J. 2014 A low-order decomposition of turbulent channel flow via resolvent analysis and convex optimization. Phys. Fluids 26, 051701.Google Scholar
Moarref, R., Sharma, A. S., Tropp, J. A. & McKeon, B. J. 2013 Model-based scaling and prediction of the streamwise energy intensity in high-Reynolds number turbulent channels. J. Fluid Mech. 734, 275–316.Google Scholar
Nakashima, S., Fukagata, K. & Luhar, M. 2017 Assessment of suboptimal control for turbulent friction reduction via resolvent analysis. J. Fluid Mech. 828, 496–526.Google Scholar
Reynolds, W. C. & Tiederman, W. G. 1967 Stability of turbulent channel flow, with application to Malkus’s theory. J. Fluid Mech. 27, 253–272.Google Scholar
Sharma, A. S. & McKeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.Google Scholar
Taira, K., Brunton, S. L., Dawson, S. T. M., Rowley, C. W., Colonius, T., McKeon, B. J., Schmidt, O. T., Gordeyev, S, Theofilis, V. & Ukeiley, L. S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55, 4013–4041.Google Scholar
Tritton, D. J. 1992 Stabilization and destabilization of turbulent shear flow in a rotating fluid. J. Fluid Mech. 241, 503–523.Google Scholar
Wallin, S., Grundestam, O. & Johansson, A. V. 2013 Laminarization mechanisms and extreme-amplitude states in rapidly rotating plane channel flow. J. Fluid Mech. 730, 177–199.Google Scholar
Weideman, J. A. & Reddy, S. C. 2000 A Matlab differentiation matrix suite. ACM Trans. Math. Softw. 26, 465–519.Google Scholar
Wu, H. & Kasagi, N. 2004 Effects of arbitrary direction system rotation on turbulent channel flow. Phys. Fluids 16, 979–990.Google Scholar
Xia, Z., Shi, Y. & Chen, S. 2016 Direct numerical simulation of turbulent channel flow with spanwise rotation. J. Fluid Mech. 788, 42–56.Google Scholar
Yang, Y. T. & Wu, J. Z. 2012 Channel turbulence with spanwise rotation studied using helical wave decomposition. J. Fluid Mech. 692, 137–152.Google Scholar