Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T19:10:35.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Reciprocal swimming at intermediate Reynolds number

Published online by Cambridge University Press:  18 November 2022

Nicholas J. Derr Open the ORCID record for Nicholas J. Derr [Opens in a new window] ,
Thomas Dombrowski ,
Chris H. Rycroft Open the ORCID record for Chris H. Rycroft [Opens in a new window]  and
Daphne Klotsa Open the ORCID record for Daphne Klotsa [Opens in a new window]
Nicholas J. Derr*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
Thomas Dombrowski
Affiliation:
Department of Applied Physical Sciences, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA
Chris H. Rycroft
Affiliation:
Department of Mathematics, University of Wisconsin–Madison, Madison, WI 53706, USA Computational Research Division, Lawrence Berkeley Laboratory, Berkeley, CA 94720, USA
Daphne Klotsa
Affiliation:
Department of Applied Physical Sciences, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

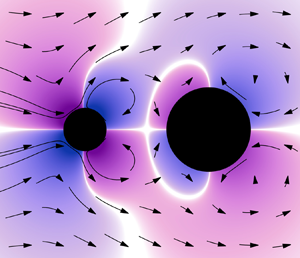
In Stokes flow, Purcell's scallop theorem forbids objects with time-reversible (reciprocal) swimming strokes from moving. In the presence of inertia, this restriction is eased and reciprocally deforming bodies can swim. A number of recent works have investigated dimer models that swim reciprocally at intermediate Reynolds numbers ${\textit Re} \approx 1$–1000. These show interesting results (e.g. switches of the swim direction as a function of inertia) but the results vary and seem to be case specific. Here, we introduce a general model and investigate the behaviour of an asymmetric spherical dimer of oscillating length for small-amplitude motion at intermediate ${\textit {Re}}$. In our analysis we make the important distinction between particle and fluid inertia, both of which need to be considered separately. We asymptotically expand the Navier–Stokes equations in the small-amplitude limit to obtain a system of linear partial differential equations. Using a combination of numerical (finite element) and analytical (reciprocal theorem, method of reflections) methods we solve the system to obtain the dimer's swim speed and show that there are two mechanisms that give rise to motion: boundary conditions (an effective slip velocity) and Reynolds stresses. Each mechanism is driven by two classes of sphere–sphere interactions, between one sphere's motion and (1) the oscillating background flow induced by the other's motion, and (2) a geometric asymmetry induced by the other's presence. We can thus unify and explain behaviours observed in other works. Our results show how sensitive, counterintuitive and rich motility is in the parameter space of finite inertia of particles and fluid.

JFM classification

Biological Fluid Dynamics: Propulsion
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , A8
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Acheson, D.J. 1990 Elementary fluid dynamics. Clarendon Press; Oxford University Press.Google Scholar
Alassar, R.S. & Badr, H.M. 1997 Oscillating viscous flow over a sphere. Comput. Fluids 26 (7), 661–682.CrossRefGoogle Scholar
Balay, S., et al. 2021 a PETSc/TAO users manual. Tech. Rep. ANL-21/39 - Revision 3.16. Argonne National Laboratory.Google Scholar
Balay, S., et al. 2021 b PETSc Web page. https://petsc.org/.Google Scholar
Balay, S., Gropp, W.D., McInnes, L.C. & Smith, B.F. 1997 Efficient management of parallelism in object oriented numerical software libraries. In Modern Software Tools in Scientific Computing (ed. E. Arge, A.M. Bruaset & H.P. Langtangen), pp. 163–202. Birkhäuser.CrossRefGoogle Scholar
Bartol, I.K., Krueger, P.S., Stewart, W.J. & Thompson, J.T. 2009 Pulsed jet dynamics of squid hatchlings at intermediate Reynolds numbers. J. Expl Biol. 212 (10), 1506–1518.CrossRefGoogle ScholarPubMed
Becker, A.D., Masoud, H., Newbolt, J.W., Shelley, M. & Ristroph, L. 2015 Hydrodynamic schooling of flapping swimmers. Nat. Commun. 6, 8514.CrossRefGoogle ScholarPubMed
Becker, L.E., Koehler, S.A. & Stone, H.A. 2003 On self-propulsion of micro-machines at low Reynolds number: Purcell's three-link swimmer. J. Fluid Mech. 490, 15–35.CrossRefGoogle Scholar
Bet, B., Boosten, G., Dijkstra, M. & van Roij, R. 2017 Efficient shapes for microswimming: from three-body swimmers to helical flagella. J. Chem. Phys. 146 (8), 084904.CrossRefGoogle ScholarPubMed
Chang, E.J. & Maxey, M.R. 1994 Unsteady flow about a sphere at low to moderate Reynolds number. Part 1. Oscillatory motion. J. Fluid Mech. 277, 347–379.CrossRefGoogle Scholar
Chang, E.J. & Maxey, M.R. 1995 Unsteady flow about a sphere at low to moderate Reynolds number. Part 2. Accelerated motion. J. Fluid Mech. 303, 133–153.CrossRefGoogle Scholar
Childress, S. 1981 Mechanics of Swimming and Flying. Cambridge University Press.CrossRefGoogle Scholar
Coenen, W. 2016 Steady streaming around a cylinder pair. Proc. R. Soc. A 472 (2195), 20160522.CrossRefGoogle Scholar
Collis, J.F., Chakraborty, D. & Sader, J.E. 2017 Autonomous propulsion of nanorods trapped in an acoustic field. J. Fluid Mech. 825, 29–48.CrossRefGoogle Scholar
Daghooghi, M. & Borazjani, I. 2015 The hydrodynamic advantages of synchronized swimming in a rectangular pattern. Bioinspir. Biomim. 10 (5), 056018.CrossRefGoogle Scholar
Dombrowski, T., Jones, S.K., Katsikis, G., Bhalla, A.P.S., Griffith, B.E. & Klotsa, D. 2019 Transition in swimming direction in a model self-propelled inertial swimmer. Phys. Rev. Fluids 4 (2), 021101.CrossRefGoogle Scholar
Dombrowski, T. & Klotsa, D. 2020 Kinematics of a simple reciprocal model swimmer at intermediate Reynolds numbers. Phys. Rev. Fluids 5 (6), 063103.CrossRefGoogle Scholar
Dray, T. 1985 The relationship between monopole harmonics and spin-weighted spherical harmonics. J. Math. Phys. 26 (5), 1030–1033.CrossRefGoogle Scholar
Durlofsky, L. & Brady, J.F. 1987 Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 30 (11), 3329–3341.CrossRefGoogle Scholar
Felderhof, B.U. 2016 Effect of fluid inertia on the motion of a collinear swimmer. Phys. Rev. E 94 (6), 063114.CrossRefGoogle ScholarPubMed
Felderhof, B.U. & Jones, R.B. 1987 Addition theorems for spherical wave solutions of the vector Helmholtz equation. J. Math. Phys. 28 (4), 836–839.CrossRefGoogle Scholar
Felderhof, B.U. & Jones, R.B. 1994 Inertial effects in small-amplitude swimming of a finite body. Physica A 202 (1), 94–118.CrossRefGoogle Scholar
Felderhof, B.U. & Jones, R.B. 2017 Swimming of a sphere in a viscous incompressible fluid with inertia. Fluid Dyn. Res. 49 (4), 045510.CrossRefGoogle Scholar
Felderhof, B.U. & Jones, R.B. 2019 Effect of fluid inertia on swimming of a sphere in a viscous incompressible fluid. Eur. J. Mech. B/Fluids 75, 312–326.CrossRefGoogle Scholar
Felderhof, B.U. & Jones, R.B. 2021 Swimming of a uniform deformable sphere in a viscous incompressible fluid with inertia. Eur. J. Mech. B/Fluids 85, 58–67.CrossRefGoogle Scholar
Feldmann, D., Das, R. & Pinchasik, B.-E. 2021 How can interfacial phenomena in nature inspire smaller robots. Adv. Mater. Interfaces 8 (1), 2001300.CrossRefGoogle Scholar
Fuiman, L.A. & Webb, P.W. 1988 Ontogeny of routine swimming activity and performance in zebra danios (Teleostei: Cyprinidae). Anim. Behav. 36 (1), 250–261.CrossRefGoogle Scholar
Gazzola, M., Argentina, M. & Mahadevan, L. 2014 Scaling macroscopic aquatic locomotion. Nat. Phys. 10 (10), 758–761.CrossRefGoogle Scholar
Gazzola, M., Tchieu, A.A., Alexeev, D., de Brauer, A. & Koumoutsakos, P. 2016 Learning to school in the presence of hydrodynamic interactions. J. Fluid Mech. 789, 726–749.CrossRefGoogle Scholar
Gonzalez-Rodriguez, D. & Lauga, E. 2009 Reciprocal locomotion of dense swimmers in Stokes flow. J. Phys.: Condens. Matter 21 (20), 204103.Google ScholarPubMed
Happel, J. & Brenner, H. 2012 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, vol. 1. Springer.Google Scholar
Hemelrijk, C.K., Reid, D.A.P., Hildenbrandt, H. & Padding, J.T. 2015 The increased efficiency of fish swimming in a school. Fish Fish. 16 (3), 511–521.CrossRefGoogle Scholar
Herschlag, G. & Miller, L. 2011 Reynolds number limits for jet propulsion: a numerical study of simplified jellyfish. J. Theor. Biol. 285 (1), 84–95.CrossRefGoogle ScholarPubMed
Hubert, M., Trosman, O., Collard, Y., Sukhov, A., Harting, J., Vandewalle, N. & Smith, A.-S. 2021 Scallop theorem and swimming at the mesoscale. Phys. Rev. Lett. 126 (22), 224501.CrossRefGoogle ScholarPubMed
Iliev, O., Lazarov, R. & Willems, J. 2011 Variational multiscale finite element method for flows in highly porous media. Multiscale Model. Simul. 9 (4), 1350–1372.CrossRefGoogle Scholar
Kim, S. & Russel, W.B. 1985 The hydrodynamic interactions between two spheres in a Brinkman medium. J. Fluid Mech. 154, 253–268.CrossRefGoogle Scholar
Klotsa, D. 2019 As above, so below, and also in between: mesoscale active matter in fluids. Soft Matt. 15 (44), 8946–8950.CrossRefGoogle ScholarPubMed
Klotsa, D., Baldwin, K.A., Hill, R.J.A., Bowley, R.M. & Swift, M.R. 2015 Propulsion of a two-sphere swimmer. Phys. Rev. Lett. 115 (24), 248102.CrossRefGoogle ScholarPubMed
Kotas, C.W., Yoda, M. & Rogers, P.H. 2007 Visualization of steady streaming near oscillating spheroids. Exp. Fluids 42 (1), 111–121.CrossRefGoogle Scholar
Lauga, E. 2007 Continuous breakdown of Purcell's scallop theorem with inertia. Phys. Fluids 19 (6), 061703.CrossRefGoogle Scholar
Lauga, E. 2011 Life around the scallop theorem. Soft Matt. 7 (7), 3060–3065.CrossRefGoogle Scholar
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.CrossRefGoogle Scholar
Li, X.S. 2005 An overview of SuperLU: algorithms, implementation, and user interface. ACM Trans. Math. Softw. 31 (3), 302–325.CrossRefGoogle Scholar
Lighthill, M.J. 1960 Note on the swimming of slender fish. J. Fluid Mech. 9 (2), 305–317.CrossRefGoogle Scholar
Lippera, K., Dauchot, O., Michelin, S. & Benzaquen, M. 2019 No net motion for oscillating near-spheres at low Reynolds numbers. J. Fluid Mech. 866, R1.CrossRefGoogle Scholar
Liu, B. & Bhattacharya, S. 2020 Vector field solution for Brinkman equation in presence of disconnected spheres. Phys. Rev. Fluids 5, 104303.CrossRefGoogle Scholar
Maertens, A.P., Gao, A. & Triantafyllou, M.S. 2017 Optimal undulatory swimming for a single fish-like body and for a pair of interacting swimmers. J. Fluid Mech. 813, 301–345.CrossRefGoogle Scholar
McHenry, M.J., Azizi, E. & Strother, J.A. 2003 The hydrodynamics of locomotion at intermediate Reynolds numbers: undulatory swimming in ascidian larvae (Botrylloides sp.). J. Expl Biol. 206 (2), 327–343.CrossRefGoogle Scholar
Nachtigall, W. 2001 Some aspects of Reynolds number effects in animals. Math. Meth. Appl. Sci. 24, 1401–1408.CrossRefGoogle Scholar
Nadal, F. & Lauga, E. 2014 Asymmetric steady streaming as a mechanism for acoustic propulsion of rigid bodies. Phys. Fluids 26 (8), 82001.CrossRefGoogle Scholar
Najafi, A. & Golestanian, R. 2004 Simple swimmer at low Reynolds number: three linked spheres. Phys. Rev. E 69 (6), 062901.CrossRefGoogle ScholarPubMed
Nguyen, Q.M., Oza, A.U., Abouezzi, J., Sun, G., Childress, S., Frederick, C. & Ristroph, L. 2021 Flow rectification in loopy network models of bird lungs. Phys. Rev. Lett. 126, 114501.CrossRefGoogle ScholarPubMed
Otto, F., Riegler, E.K. & Voth, G.A. 2008 Measurements of the steady streaming flow around oscillating spheres using three dimensional particle tracking velocimetry. Phys. Fluids 20 (9), 093304.CrossRefGoogle Scholar
Pacheco-Martinez, H.A., Liao, L., Hill, R.J.A., Swift, M.R. & Bowley, R.M. 2013 Spontaneous orbiting of two spheres levitated in a vibrated liquid. Phys. Rev. Lett. 110 (15), 154501.CrossRefGoogle Scholar
Park, S.-J. et al. 2016 Phototactic guidance of a tissue-engineered soft-robotic ray. Science 353 (6295), 158–162.CrossRefGoogle ScholarPubMed
Pedley, T.J. 2016 Spherical squirmers: models for swimming micro-organisms. IMA J. Appl. Maths 81 (3), 488–521.CrossRefGoogle Scholar
Purcell, E.M. 1977 Life at low Reynolds number. Am. J. Phys. 45 (1), 3–11.CrossRefGoogle Scholar
Rednikov, A.Y. & Sadhal, S.S. 2004 Steady streaming from an oblate spheroid due to vibrations along its axis. J. Fluid Mech. 499, 345–380.CrossRefGoogle Scholar
Riley, N. 1966 On a sphere oscillating in a viscous fluid. Q. J. Mech. Appl. Maths 19 (4), 461–472.CrossRefGoogle Scholar
Swift, M.R., Klotsa, D., Wright, H.S., Bowley, R.M. & King, P.J. 2009 The dynamics of spheres in oscillatory fluid flows. AIP Conf. Proc. 1039–1042.CrossRefGoogle Scholar
Tatsuno, M. 1973 Circulatory streaming around an oscillating circular cylinder at low Reynolds numbers. J. Phys. Soc. Japan 35 (3), 915–920.CrossRefGoogle Scholar
Tatsuno, M. 1981 Secondary flow induced by a circular cylinder performing unharmonic oscillations. J. Phys. Soc. Japan 50 (1), 330–337.CrossRefGoogle Scholar
Taylor, G.I. 1951 Analysis of the swimming of microscopic organisms. Proc. R. Soc. Lond. A 209 (1099), 447–461.Google Scholar
Vogel, S. 2008 Modes and scaling in aquatic locomotion. Integr. Compar. Biol. 48 (6), 702–712.CrossRefGoogle ScholarPubMed
Wright, H.S., Swift, M.R. & King, P.J. 2008 Migration of an asymmetric dimer in oscillatory fluid flow. Phys. Rev. E 78, 036311.CrossRefGoogle ScholarPubMed
Wu, T.Y. 2011 Fish swimming and bird/insect flight. Annu. Rev. Fluid Mech. 43 (1), 25–58.CrossRefGoogle Scholar
Ziegler, S., Hubert, M., Vandewalle, N., Harting, J. & Smith, A.-S. 2019 A general perturbative approach for bead-based microswimmers reveals rich self-propulsion phenomena. New J. Phys. 21 (11), 113017.CrossRefGoogle Scholar