Article contents
Reaction-induced Kelvin–Helmholtz instability in a layered channel flow
Published online by Cambridge University Press: 19 January 2023
Abstract
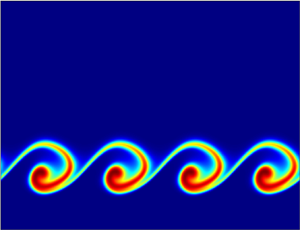
We show that a vertical viscosity stratification at a localized region caused by a chemical reaction yields an inconspicuous shear layer. A chemo-hydrodynamic Kelvin–Helmholtz instability or cat-eye-shaped morphology develops at one reaction front, while the other front diffuses steadily over time. Through linear stability and nonlinear simulations, the existence of such instabilities is established if the log-mobility ratio exceeds a critical value. We find unique scalings between the stable and unstable zones that demonstrate how the influence of variations in solute diffusion on instability can be eliminated. The observed unstable patterns agree with existing experimental results.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by



