Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T19:49:10.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Rayleigh–Bloch waves above the cutoff

Published online by Cambridge University Press:  12 April 2022

Luke G. Bennetts Open the ORCID record for Luke G. Bennetts [Opens in a new window]  and
Malte A. Peter Open the ORCID record for Malte A. Peter [Opens in a new window]
Luke G. Bennetts*
Affiliation:
School of Mathematical Sciences, University of Adelaide, Adelaide, SA 5005, Australia
Malte A. Peter
Affiliation:
Institute of Mathematics, University of Augsburg, 86135 Augsburg, Germany Centre for Advanced Analytics and Predictive Sciences (CAAPS), University of Augsburg, 86135 Augsburg, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

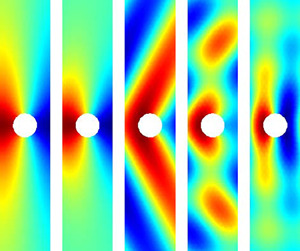
Extensions of Rayleigh–Bloch waves above the cutoff frequency are studied via the discrete spectrum of a transfer operator for a channel containing a single cylinder with quasi-periodic side-wall conditions. Above the cutoff, the Rayleigh–Bloch wavenumber becomes complex valued and an additional wavenumber appears. For small- to intermediate-radius values, the extended Rayleigh–Bloch waves are shown to connect the Neumann and Dirichlet trapped modes before embedding in the continuous spectrum. A homotopy method involving an artificial damping term is proposed to identify the discrete spectrum close to the embedding. Moreover, Rayleigh–Bloch waves vanish beyond some frequency but reappear at higher frequencies for small and large cylinders. The existence and properties of the Rayleigh–Bloch waves are connected with finite-array resonances.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave scattering Waves/Free-surface Flows: Wave-structure interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 940 , 10 June 2022 , A35
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bennetts, L.G. 2011 Wave attenuation through multiple rows of scatterers with differing periodicities. SIAM J. Appl. Maths 71 (2), 540–558.CrossRefGoogle Scholar
Bennetts, L.G., Peter, M.A. & Craster, R.V. 2018 Graded resonator arrays for spatial frequency separation and amplification of water waves. J. Fluid Mech. 854, R4.CrossRefGoogle Scholar
Bennetts, L.G., Peter, M.A. & Craster, R.V. 2019 Low-frequency wave-energy amplification in graded two-dimensional resonator arrays. Phil. Trans. R. Soc. A 377 (2156), 20190104.CrossRefGoogle ScholarPubMed
Bennetts, L.G., Peter, M.A. & Montiel, F. 2017 Localisation of Rayleigh–Bloch waves and damping of resonant loads on arrays of vertical cylinders. J. Fluid Mech. 813, 508–527.CrossRefGoogle Scholar
Bennetts, L.G. & Squire, V.A. 2009 Wave scattering by multiple rows of circular ice floes. J. Fluid Mech. 639, 213–238.CrossRefGoogle Scholar
Chaplain, G.J. & Craster, R.V. 2019 Flat lensing by graded line meta-arrays. Phys. Rev. B 99 (22), 220102(R).CrossRefGoogle Scholar
Evans, D.V. & Porter, R. 1998 Trapped modes embedded in the continuous spectrum. Q. J. Mech. Appl. Maths 51 (2), 263–274.CrossRefGoogle Scholar
Evans, D.V. & Porter, R. 1999 Trapping and near-trapping by arrays of cylinders in waves. J. Engng Maths 35, 149–179.CrossRefGoogle Scholar
Hsu, C.W., Zhen, B., Stone, A.D., Joannopoulos, J.D. & Soljačić, M. 2016 Bound states in the continuum. Nat. Rev. Mater. 1 (9), 16048.CrossRefGoogle Scholar
Linton, C.M. & McIver, P. 2007 Embedded trapped modes in water waves and acoustics. Wave Motion 45 (1–2), 16–29.CrossRefGoogle Scholar
Linton, C.M., Porter, R. & Thompson, I. 2007 Scattering by a semi-infinite periodic array and the excitation of surface waves. SIAM J. Appl. Maths 67 (5), 1233–1258.CrossRefGoogle Scholar
Linton, C.M. & Thompson, I. 2007 Resonant effects in scattering by periodic arrays. Wave Motion 44 (3), 165–175.CrossRefGoogle Scholar
Maling, B. & Craster, R.V. 2016 Whispering Bloch modes. Proc. R. Soc. A 472 (2191), 20160103.CrossRefGoogle ScholarPubMed
Maniar, H.D. & Newman, J.N. 1997 Wave diffraction by a long array of cylinders. J. Fluid Mech. 339, 309–330.CrossRefGoogle Scholar
Martin, P.A. 2006 Multiple Scattering: Interaction of Time-Harmonic Waves with N Obstacles. Cambridge University Press.CrossRefGoogle Scholar
McIver, P. 2000 Water-wave propagation through an infinite array of cylindrical structures. J. Fluid Mech. 424, 101–125.CrossRefGoogle Scholar
Montiel, F., Squire, V.A. & Bennetts, L.G. 2015 Evolution of directional wave spectra through finite regular and randomly perturbed arrays of scatterers. SIAM J. Appl. Maths 75 (2), 630–651.CrossRefGoogle Scholar
Peter, M.A. & Meylan, M.H. 2004 Infinite-depth interaction theory for arbitrary floating bodies applied to wave forcing of ice floes. J. Fluid Mech. 500, 145–167.CrossRefGoogle Scholar
Peter, M.A. & Meylan, M.H. 2007 Water-wave scattering by a semi-infinite periodic array of arbitrary bodies. J. Fluid Mech. 575, 473–494.CrossRefGoogle Scholar
Peter, M.A., Meylan, M.H. & Linton, C.M. 2006 Water-wave scattering by a periodic array of arbitrary bodies. J. Fluid Mech. 548, 237–256.CrossRefGoogle Scholar
Porter, R. & Evans, D.V. 2005 Embedded Rayleigh–Bloch surface waves along periodic rectangular arrays. Wave Motion 43 (1), 29–50.CrossRefGoogle Scholar
Porter, R. & Evans, D.V. 1999 Rayleigh–Bloch surface waves along periodic gratings and their connection with trapped modes in waveguides. J. Fluid Mech. 386, 233–258.CrossRefGoogle Scholar
Schnitzer, O., Brandão, R. & Yariv, E. 2019 Acoustics of bubbles trapped in microgrooves: from isolated subwavelength resonators to superhydrophobic metasurfaces. Phys. Rev. B 99 (19), 195155.CrossRefGoogle Scholar
Thompson, I., Linton, C.M. & Porter, R. 2008 A new approximation method for scattering by long finite arrays. Q. J. Mech. Appl. Maths 61 (3), 333–352.CrossRefGoogle Scholar
Utsunomiya, T. & Eatock Taylor, R. 1999 Trapped modes around a row of circular cylinders in a channel. J. Fluid Mech. 386, 259–279.CrossRefGoogle Scholar
Zeng, X., Yu, F., Shi, M. & Wang, Q. 2019 Fluctuation of magnitude of wave loads for a long array of bottom-mounted cylinders. J. Fluid Mech. 868, 244–285.CrossRefGoogle Scholar