Article contents
Radial viscous fingering induced by an infinitely fast chemical reaction
Published online by Cambridge University Press: 20 July 2022
Abstract
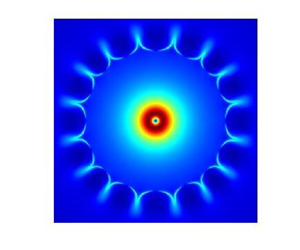
A numerical insight into the radial displacement of two viscously stable reactants undergoing an infinitely fast chemical reaction is obtained. This work broadens the numerical knowledge about the interaction between chemical reaction and hydrodynamic instability. A suitable transformation is utilised to deal with an infinite dimensionless parameter and reduce computational cost. Viscous fingering instability originates when the product has a different viscosity than the reactants. We calculate the onset time  $t_{on}$ when the instability begins to appear for different reactants by varying the log mobility ratio
$t_{on}$ when the instability begins to appear for different reactants by varying the log mobility ratio  $R_c$ and the Péclet number
$R_c$ and the Péclet number  $Pe$. Based on
$Pe$. Based on  $t_{on}$, we divide the time domain into stable and unstable zones with respect to instability. This helps to characterise reactants so as to have a flow with/without instability. For a fixed
$t_{on}$, we divide the time domain into stable and unstable zones with respect to instability. This helps to characterise reactants so as to have a flow with/without instability. For a fixed  $Pe$ and
$Pe$ and  $\vert R_c \vert$, it is found that
$\vert R_c \vert$, it is found that  $t_{on}$ is early for
$t_{on}$ is early for  $R_c > 0$ in contrast to the result for rectilinear displacement. This results in a wider stable zone for
$R_c > 0$ in contrast to the result for rectilinear displacement. This results in a wider stable zone for  $R_c < 0$. Interestingly, it is found that the stable zone can be made independent of
$R_c < 0$. Interestingly, it is found that the stable zone can be made independent of  $Pe$ by using a careful rescaling and we obtain the dependence of the onset time of instability on
$Pe$ by using a careful rescaling and we obtain the dependence of the onset time of instability on  $R_c$ and
$R_c$ and  $Pe$ as
$Pe$ as  $t_{on} \propto (\vert R_c\vert Pe^{\beta _1}-\beta _2)^{\beta _3}$ where the constant of proportionality and
$t_{on} \propto (\vert R_c\vert Pe^{\beta _1}-\beta _2)^{\beta _3}$ where the constant of proportionality and  $\beta _i$,
$\beta _i$,  $i=1,2,3$, depend upon the sign of
$i=1,2,3$, depend upon the sign of  $R_c$. In the unstable zone, we find that the length of the fingers depends upon the sign of
$R_c$. In the unstable zone, we find that the length of the fingers depends upon the sign of  $R_c$, which is not observed for any radial displacement of reactants undergoing a slow or moderately fast chemical reaction.
$R_c$, which is not observed for any radial displacement of reactants undergoing a slow or moderately fast chemical reaction.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 12
- Cited by



