Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T18:04:15.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Proposal of control laws for turbulent skin friction reduction based on resolvent analysis

Published online by Cambridge University Press:  18 March 2019

Aika Kawagoe ,
Satoshi Nakashima ,
Mitul Luhar Open the ORCID record for Mitul Luhar [Opens in a new window]  and
Koji Fukagata Open the ORCID record for Koji Fukagata [Opens in a new window]
Aika Kawagoe
Affiliation:
Department of Mechanical Engineering, Keio University, Yokohama 223-8522, Japan
Satoshi Nakashima
Affiliation:
Department of Mechanical Engineering, Keio University, Yokohama 223-8522, Japan
Mitul Luhar
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Koji Fukagata*
Affiliation:
Department of Mechanical Engineering, Keio University, Yokohama 223-8522, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper evaluates and modifies the so-called suboptimal control technique for turbulent skin friction reduction through a combination of low-order modelling and direct numerical simulation (DNS). In a previous study, Nakashima et al. (J. Fluid Mech., vol. 828, 2017, pp. 496–526) employed resolvent analysis to show that the efficacy of suboptimal control was mixed across spectral space when the streamwise wall shear stress (case ST) was used as a sensor signal, i.e. specific regions of spectral space showed drag increment. This observation suggests that drag reduction may be attained if control is applied selectively in spectral space. DNS results presented in the present study, however, do not show a significant effect on the flow with selective control. A posteriori analyses attribute this lack of efficacy to a much lower actuation amplitude in the simulations compared to model assumptions. Building on these observations, resolvent analysis is used to design and provide a preliminary assessment of modified control laws that also rely on sensing the streamwise wall shear stress. Control performance is then assessed by means of DNS. The proposed control laws generate as much as 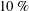$10\,\%$ drag reduction, and these results are broadly consistent with resolvent-based predictions. The physical mechanisms leading to drag reduction are assessed via conditional sampling. It is shown that the new control laws effectively suppress the near-wall quasi-streamwise vortices. A physically intuitive explanation is proposed based on a separate evaluation of clockwise and anticlockwise vortices.

JFM classification

Flow Control: Drag reduction Turbulent Flows: Turbulence control Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 810 - 840
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2003 Spectra of very large anisotropic scales in turbulent channels. Phys. Fluids 15, 41–44.Google Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.Google Scholar
Choi, J.-I. & Sung, H. J. 2002 Assessment of suboptimal control for drag reduction in turbulent channel flow. J. Turbul. 3 (29), 1–17.Google Scholar
Chung, Y. M. & Talha, T. 2011 Effectiveness of active flow control for turbulent skin friction drag reduction. Phys. Fluids 23, 025102.Google Scholar
Deng, B.-Q., Xu, C.-X., Huang, W.-X. & Cui, G.-X. 2014 Strengthened opposition control for skin-friction reduction in wall-bounded turbulent flows. J. Turbul. 15 (2), 122–143.Google Scholar
Deng, B.-Q., Huang, W.-X. & Xu, C.-X. 2016 Origin of effectiveness degradation in active drag reduction control of turbulent channel flow at Re 𝜏 = 1000. J. Turbul. 17, 758–786.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14, L73–L76.Google Scholar
Fukagata, K. & Kasagi, N. 2004 Suboptimal control for drag reduction via suppression of near-wall Reynolds shear stress. Intl J. Heat Fluid Flow 25, 341–350.10.1016/j.ijheatfluidflow.2004.02.015Google Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent channel flow by superhydrophobic surface. Phys. Fluids 18, 051703.Google Scholar
Fukagata, K., Kobayashi, M. & Kasagi, N. 2010 On the friction drag reduction effect by a control of large-scale turbulent structures. J. Fluid Sci. Technol. 5, 574–584.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanism of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hasegawa, Y. & Kasagi, N. 2011 Dissimilar control of momentum and heat transfer in a fully developed turbulent channel flow. J. Fluid Mech. 683, 57–93.Google Scholar
Hœpffner, J. & Fukagata, K. 2009 Pumping or drag reduction? J. Fluid Mech. 635, 171–187.10.1017/S0022112009007629Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuation in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 011702.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, streams and convergence zones in turbulent flows. Summer program, Center for Turbulence Research, NASA Ames/Stanford University, pp. 193–208.Google Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N. 2002 Reynolds number effect on wall turbulence: toward effective feedback control. Intl J. Heat Fluid Flow 23, 678–689.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structure near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jung, W., Mangiavacchi, N. & Akhavan, R. 1992 Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Phys. Fluids 4, 1605–1607.Google Scholar
Kasagi, N., Suzuki, T. & Fukagata, K. 2009 Microelectromechanical systems-based feedback control of turbulence skin friction reduction. Annu. Rev. Fluid Mech. 41, 231–251.Google Scholar
Kajishima, T. & Taira, K. 2017 Computational Fluid Dynamics. Springer.Google Scholar
Kim, J. & Lim, J. 2000 A linear process in wall-bounded turbulent shear flows. Phys. Fluids 12, 1885–1888.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed turbulent flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Rundstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Koumoutsakos, P. 1999 Vorticity flux control for a turbulent channel flow. Phys. Fluids 11, 248–250.Google Scholar
Lee, C., Kim, J. & Choi, H. 1998 Suboptimal control of turbulent channel flow for drag reduction. J. Fluid Mech. 358, 245–258.Google Scholar
Lee, J. 2015 Opposition control of turbulent wall-bounded flow using upstream sensor. J. Mech. Sci. Technol. 29, 4729–4735.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2014 Opposition control within the resolvent analysis framework. J. Fluid Mech. 749, 597–626.Google Scholar
Luhar, M., Sharma, A. S. & Mckeon, B. J. 2015 A framework for studying the effect of compliant surfaces on wall turbulence. J. Fluid Mech. 768, 415–441.Google Scholar
Luhar, M., Sharma, A. S. & Mckeon, B. J. 2016 On the design of optimal compliant walls for turbulence control. J. Turbul. 17, 787–806.Google Scholar
Mamori, H., Iwamoto, K. & Murata, A. 2014 Effect of the parameters of traveling waves created by blowing and suction on the relaminarization phenomena in fully developed turbulent channel flow. Phys. Fluids 26, 015101.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
McKeon, B. J., Jacobi, I. & Sharma, A. S. 2013 Experimental manipulation of wall turbulence: a systems approach. Phys. Fluids 25, 031301.Google Scholar
McKeon, B. J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1–P86.Google Scholar
Min, T., Kang, S. M., Speyer, J. L. & Kim, J. 2006 Sustained sub-laminar drag in a fully developed channel flow. J. Fluid Mech. 558, 309–318.Google Scholar
Moarref, R., Sharma, A. S., Tropp, J. A. & McKeon, B. J. 2013 Model-based scaling and prediction of the streamwise energy intensity in high-Reynolds number turbulent channels. J. Fluid Mech. 734, 275–316.Google Scholar
Moser, R., Kim, J. & Mansour, N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.Google Scholar
Morimoto, K., Iwamoto, K., Suzuki, Y. & Kasagi, N. 2002 Genetic algorithm-based optimization of feed back control scheme for wall turbulence. In Proc. 3rd Symp. Smart Control of Turbulence, Tokyo, pp. 107–113.Google Scholar
Nakanishi, R., Mamori, H. & Fukagata, K. 2012 Relaminarization of turbulent channel flow using traveling wave-like wall deformation. Intl J. Heat Fluid Flow 35, 152–159.Google Scholar
Nakashima, S., Fukagata, K. & Luhar, M. 2017 Assessment of suboptimal control for turbulent skin friction reduction via resolvent analysis. J. Fluid Mech. 828, 496–526.Google Scholar
Nakashima, S., Luhar, M. & Fukagata, K. 2019 Reconsideration of spanwise rotating turbulent channel flows via resolvent analysis. J. Fluid Mech. 861, 200–222.Google Scholar
Quadrio, M., Ricco, P. & Viotti, C. 2009 Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. J. Fluid Mech. 627, 161–178.Google Scholar
Rebbeck, H. & Choi, K.-S. 2001 Opposition control of near-wall turbulence with a piston-type actuator. Phys. Fluids 13, 2142–2145.Google Scholar
Rebbeck, H. & Choi, K.-S. 2006 A wind-tunnel experiment on real-time opposition control of turbulence. Phys. Fluids 18, 035103.Google Scholar
Robinson, S. K. 1991 Coherent motions in turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Sharma, A. S. & McKeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Viotti, C., Quadrio, M. & Luchini, P. 2009 Streamwise oscillation of spanwise velocity at the wall of a channel for turbulent drag reduction. Phys. Fluids 21, 115109.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Walsh, M. J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21, 485–486.Google Scholar
White, C. M. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.Google Scholar
Yoshino, T., Suzuki, Y. & Kasagi, N. 2008 Drag reduction of turbulence air channel flow with distributed micro sensors and actuators. J. Fluid Sci. Technol. 3, 137–148.Google Scholar