Article contents
Progressive flexural–gravity waves with constant vorticity
Published online by Cambridge University Press: 23 October 2020
Abstract
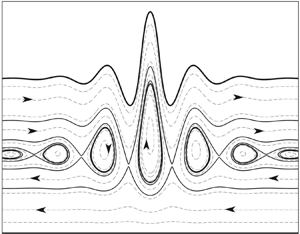
This paper is concerned with the interaction of vertically sheared currents with two-dimensional flexural–gravity waves in finite depth. A third-order Stokes expansion is carried out and fully nonlinear computations are performed for symmetric, steadily travelling waves on a linear shear current. For upstream periodic waves, two global bifurcation mechanisms are discovered. Both branches bifurcate from infinitesimal periodic waves, with one stopping at another infinitesimal wave of different phase speed, and the other terminating at a stationary configuration. Generalised solitary waves are found for downstream waves. More surprisingly, the central pulse of the generalised solitary wave can become wide and flat as the computational domain is enlarged. This provides strong evidence for the existence of wave fronts in single-layer free-surface waves. Particle trajectories and streamline structures are studied numerically for the fully nonlinear equations. Two patterns, closed orbits and pure horizontal transport, are observed for both periodic and solitary waves in moving frames. The most striking phenomenon is the existence of net vertical transport of particles beneath some solitary waves due to wave–current interactions. The streamline patterns alternate between net vertical transport and a closed orbit, resulting in the formation of a series of nested cat's-eye structures.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 10
- Cited by



