Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Wenkang
Pan, Chong
and
Wang, Jinjun
2018.
Wall-Normal Variation of Spanwise Streak Spacing in Turbulent Boundary Layer With Low-to-Moderate Reynolds Number.
Entropy,
Vol. 21,
Issue. 1,
p.
24.
Hu, Ruifeng
and
Zheng, Xiaojing
2018.
Energy contributions by inner and outer motions in turbulent channel flows.
Physical Review Fluids,
Vol. 3,
Issue. 8,
Yao, Jie
Chen, Xi
and
Hussain, Fazle
2019.
Reynolds number effect on drag control via spanwise wall oscillation in turbulent channel flows.
Physics of Fluids,
Vol. 31,
Issue. 8,
Wu, Sicong
Christensen, Kenneth T.
and
Pantano, Carlos
2019.
Modelling smooth- and transitionally rough-wall turbulent channel flow by leveraging inner–outer interactions and principal component analysis.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
407.
Wang, Hongping
Yang, Zixuan
Li, Binglin
and
Wang, Shizhao
2020.
Predicting the near-wall velocity of wall turbulence using a neural network for particle image velocimetry.
Physics of Fluids,
Vol. 32,
Issue. 11,
Wang, Hai-Ning
Huang, Wei-Xi
and
Xu, Chun-Xiao
2020.
Space–time characteristics of turbulence in minimal flow units.
Physics of Fluids,
Vol. 32,
Issue. 12,
Wang, Limin
Hu, Ruifeng
and
Zheng, Xiaojing
2020.
A comparative study on the large-scale-resolving capability of wall-modeled large-eddy simulation.
Physics of Fluids,
Vol. 32,
Issue. 3,
Zhang, Bo-Yuan
Huang, Wei-Xi
and
Xu, Chun-Xiao
2020.
Rough-wall turbulence in minimal flow units with rod-roughened walls.
Physics of Fluids,
Vol. 32,
Issue. 11,
Yang, Bowen
Jin, Guodong
Wu, Ting
Yang, Zixuan
and
He, Guowei
2020.
Numerical implementation and evaluation of resolvent-based estimation for space–time energy spectra in turbulent channel flows.
Acta Mechanica Sinica,
Vol. 36,
Issue. 4,
p.
775.
Deng, Bing-Qing
Yang, Zixuan
Xuan, Anqing
and
Shen, Lian
2020.
Localizing effect of Langmuir circulations on small-scale turbulence in shallow water.
Journal of Fluid Mechanics,
Vol. 893,
Issue. ,
Wang, Hai-Ning
Huang, Wei-Xi
and
Xu, Chun-Xiao
2021.
Synthetic near-wall small-scale turbulence and its application in wall-modeled large-eddy simulation.
Physics of Fluids,
Vol. 33,
Issue. 9,
Zhang, Bo-Yuan
Huang, Wei-Xi
and
Xu, Chun-Xiao
2021.
A near-wall predictive model for passive scalars using minimal flow unit.
Physics of Fluids,
Vol. 33,
Issue. 4,
Davis, Ethan A.
Mirfendereski, Siamak
and
Park, Jae Sung
2021.
On the Comparison of Flow Physics between Minimal and Extended Flow Units in Turbulent Channels.
Fluids,
Vol. 6,
Issue. 5,
p.
192.
Wang, Limin
Hu, Ruifeng
and
Zheng, Xiaojing
2021.
A scaling improved inner–outer decomposition of near-wall turbulent motions.
Physics of Fluids,
Vol. 33,
Issue. 4,
Wang, Hai-Ning
Huang, Wei-Xi
and
Xu, Chun-Xiao
2021.
Off-wall boundary conditions for large-eddy simulation based on near-wall turbulence prediction.
Physics of Fluids,
Vol. 33,
Issue. 4,
Wang, Hongping
Yang, Zixuan
Wu, Ting
and
Wang, Shizhao
2021.
Coherent structures associated with interscale energy transfer in turbulent channel flows.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Chen, Yuandong
Wang, Xiaoning
Duan, Lishu
and
Wang, Jianchun
2022.
Effect of heat source on kinetic energy transfer in compressible homogeneous shear turbulence.
Physics of Fluids,
Vol. 34,
Issue. 12,
Zhang, Qing-fu
Pan, Chong
and
Wang, Jin-jun
2022.
De-asymmetry of small-scale motions in wall-bounded turbulence.
Physics of Fluids,
Vol. 34,
Issue. 6,
Yu, Ming
and
Xu, Chunxiao
2022.
Predictive models for near-wall velocity and temperature fluctuations in supersonic wall-bounded turbulence.
Journal of Fluid Mechanics,
Vol. 937,
Issue. ,
Yu, Ming
Liu, Peng Xin
Fu, Ya Lu
Tang, Zhi Gong
and
Yuan, Xian Xu
2022.
Wall shear stress, pressure and heat flux fluctuations in compressible wall-bounded turbulence. II. Spectra, correlation and nonlinear interactions.
Physics of Fluids,
Vol. 34,
Issue. 6,
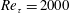 $Re_{\unicode[STIX]{x1D70F}}=2000$ to sustain healthy turbulence below
$Re_{\unicode[STIX]{x1D70F}}=2000$ to sustain healthy turbulence below 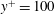 $y^{+}=100$. Turbulence intensities are compared with those of the motions at the same scales as the minimal channel in the full-sized channel at
$y^{+}=100$. Turbulence intensities are compared with those of the motions at the same scales as the minimal channel in the full-sized channel at 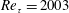 $Re_{\unicode[STIX]{x1D70F}}=2003$ (Hoyas & Jiménez, Phys. Fluids, vol. 20 (10), 2008, article 101511). They show good agreement in
$Re_{\unicode[STIX]{x1D70F}}=2003$ (Hoyas & Jiménez, Phys. Fluids, vol. 20 (10), 2008, article 101511). They show good agreement in 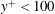 $y^{+}<100$. The universal signals for the three velocity components similar to that in the predictive model of Marusic et al. (Science, vol. 329 (5988), 2010, pp. 193–196) are extracted from the DNS data of the full-sized channel. They correspond well to the near-wall velocity fluctuations in the minimal flow unit (MFU). The predictive models for the three components of near-wall velocity fluctuations are proposed based on the MFU data. The predicted turbulence intensities as well as the joint probability density functions of velocity fluctuations agree well with the DNS results of the full-sized channel turbulence.
$y^{+}<100$. The universal signals for the three velocity components similar to that in the predictive model of Marusic et al. (Science, vol. 329 (5988), 2010, pp. 193–196) are extracted from the DNS data of the full-sized channel. They correspond well to the near-wall velocity fluctuations in the minimal flow unit (MFU). The predictive models for the three components of near-wall velocity fluctuations are proposed based on the MFU data. The predicted turbulence intensities as well as the joint probability density functions of velocity fluctuations agree well with the DNS results of the full-sized channel turbulence.