We revisit the classical but as yet unresolved problem of predicting the strength of breaking 2-D and 3-D gravity water waves, as quantified by the amount of wave energy dissipated per breaking event. Following Duncan (J. Fluid Mech., vol. 126, 1983, pp. 507–520), the wave energy dissipation rate per unit length of breaking crest may be related to the fifth moment of the wave speed and the non-dimensional breaking strength parameter 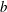$b$. We use a finite-volume Navier–Stokes solver with large-eddy simulation resolution and volume-of-fluid surface reconstruction (Derakhti & Kirby, J. Fluid Mech., vol. 761, 2014a, pp. 464–506; J. Fluid Mech., vol. 790, 2016, pp. 553–581) to simulate nonlinear wave evolution, with a strong focus on breaking onset and postbreaking behaviour for representative cases of wave packets with breaking due to dispersive focusing and modulational instability. The present study uses these results to investigate the relationship between the breaking strength parameter 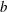$b$ and the breaking onset parameter 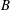$B$ proposed recently by Barthelemy et al. (J. Fluid Mech., vol. 841, 2018, pp. 463–488). The latter, formed from the local energy flux normalized by the local energy density and the local crest speed, simplifies, on the wave surface, to the ratio of fluid speed to crest speed. Following a wave crest, when 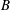$B$ exceeds a generic threshold value at the wave crest (Barthelemy et al. 2018), breaking is imminent. We find a robust relationship between the breaking strength parameter 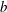$b$ and the rate of change of breaking onset parameter 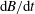$\text{d}B/\text{d}t$ at the wave crest, as it transitions through the generic breaking onset threshold (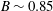$B\sim 0.85$), scaled by the local period of the breaking wave. This result significantly refines previous efforts to express 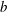$b$ in terms of a wave packet steepness parameter, which is difficult to define robustly and which does not provide a generically accurate forecast of the energy dissipated by breaking.