Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T11:22:59.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Poleward propagation of near-inertial waves induced by fluctuating winds over a baroclinically unstable zonal jet

Published online by Cambridge University Press:  17 November 2017

Marine Tort Open the ORCID record for Marine Tort [Opens in a new window]  and
Kraig B. Winters
Marine Tort*
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92093, USA
Kraig B. Winters
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92093, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the excitation and radiation of near-inertial internal gravity waves continuously excited by a latitudinally confined temporally fluctuating wind in a numerical model of a stratified ocean on a 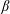$\unicode[STIX]{x1D6FD}$-plane at mid-latitude. The surface wind forcing contains both high- and low-frequency components which excite propagating waves and a baroclinically unstable zonal jet respectively. Wentzel–Kramers–Brillouin (WKB) ray theory implies that near-inertial waves propagate strictly towards the equator. We seek to refine this view here by (i) adding the non-traditional Coriolis force (accounting for the horizontal component of the Earth’s rotation) into the equations of motion, in order to allow poleward sub-inertial propagation to occur, and (ii) relaxing the conceptual constraint of no zonal variability, to allow the zonal jet to undergo instability, to meander and to sustain an active field of mesoscale eddies, potentially impacting the excitation of near-inertial waves. The key results are that, while (i) permits weakly stratified waveguides with sub-inertial poleward wave propagation to develop in accord with theory, the sub-inertial energy flux observed is very small compared with the equatorward flux. Thus, in terms of energy radiated from the storm track, non-traditional effects are small for wind-driven near-inertial waves. The consequences of (ii) are much more pronounced. Refinement (ii) produces a radiating wave field that is bidirectional, i.e. with both poleward and equatorward components. We show that the presence of regions of significant background vorticity with horizontal scales significantly smaller than the width of the storm track provides the scale selection mechanism to excite waves with sufficiently super-inertial frequencies to propagate poleward distances of the order of 1000 km.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 834 , 10 January 2018 , pp. 510 - 530
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alford, M. H. 2003 Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature 423 (6936), 159–162.Google Scholar
Alford, M. H., MacKinnon, J. A., Simmons, H. L. & Nash, J. D. 2016 Near-inertial internal gravity waves in the ocean. Annu. Rev. Marine Sci. 8 (1), 95–123.Google Scholar
Anderson, D. L. T. & Gill, A. E. 1979 𝛽-dispersion of inertial waves. J. Geophys. Res. 84 (C4), 1836–1842.CrossRefGoogle Scholar
Barkan, R., Winters, K. B. & McWilliams, J. C. 2017 Stimulated imbalance and the enhancement of eddy kinetic energy dissipation by internal waves. J. Phys. Oceanogr. 47 (1), 181–198.Google Scholar
Cessi, P., Young, W. R. & Polton, J. A. 2006 Control of large-scale heat transport by small-scale mixing. J. Phys. Oceanogr. 36 (10), 1877–1894.Google Scholar
Chant, R. J. 2001 Evolution of near-inertial waves during an upwelling event on the New Jersey inner shelf. J. Phys. Oceanogr. 31 (3), 746–764.Google Scholar
Chen, C., Reid, R. O. & Nowlin, W. D. 1996 Near-inertial oscillations over the Texas–Louisiana shelf. J. Geophys. Res. Oceans 101 (C2), 3509–3524.Google Scholar
Danioux, E., Klein, P. & Rivière, P. 2008 Propagation of wind energy into the deep ocean through a fully turbulent mesoscale eddy field. J. Phys. Oceanogr. 38 (10), 2224–2241.Google Scholar
Danioux, E. & Vanneste, J. 2016 Near-inertial-wave scattering by random flows. Phys. Rev. Fluids 1, 033701.Google Scholar
D’Asaro, E. A. 1985 The energy flux from the wind to near-inertial motions in the surface mixed layer. J. Phys. Oceanogr. 15 (8), 1043–1059.Google Scholar
D’Asaro, E. A., Eriksen, C. C., Levine, M. D., Paulson, C. A., Niiler, P. & Van Meurs, P. 1995 Upper-ocean inertial currents forced by a strong storm. Part I: data and comparisons with linear theory. J. Phys. Oceanogr. 25 (11), 2909–2936.Google Scholar
Dellar, P. J. 2011 Variations on a beta-plane: derivation of non-traditional beta-plane equations from Hamilton’s principle on a sphere. J. Fluid Mech. 674, 174–195.CrossRefGoogle Scholar
Eckart, C. 1960 Hydrodynamics of Oceans and Atmospheres. Pergamon.Google Scholar
Fu, L.-L. 1981 Observations and models of inertial waves in the deep ocean. Rev. Geophys. 19 (1), 141–170.Google Scholar
Garrett, C. 2001 What is the near-inertial band and why is it different from the rest of the internal wave spectrum? J. Phys. Oceanogr. 31 (4), 962–971.2.0.CO;2>CrossRefGoogle Scholar
Garrett, C. J. & Munk, W. G. 1972 Space–time scales of internal waves. Geophys. Fluid Dyn. 3, 225–264.Google Scholar
Gerkema, T. & Shrira, V. I. 2005a Near-inertial waves in the ocean: beyond the traditional approximation. J. Fluid Mech. 529, 195–219.Google Scholar
Gerkema, T. & Shrira, V. I. 2005b Near-inertial waves on the a non-traditional 𝛽-plane. J. Geophys. Res. 110 (C1), 1003.Google Scholar
Gerkema, T., Zimmerman, J. T. F., Maas, L. R. M. & Van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46 (2), 2004.Google Scholar
Gill, A. E. 1984 On the behavior of internal waves in the wakes of storms. J. Phys. Oceanogr. 14 (7), 1129–1151.2.0.CO;2>CrossRefGoogle Scholar
Grimshaw, R. H. J. 1975 A note on the 𝛽-plane approximation. Tellus 27 (4), 351–357.Google Scholar
Hazewinkel, J. & Winters, K. B. 2011 PSI of the internal tide on a 𝛽-plane: flux divergence and near-inertial wave propagation. J. Phys. Oceanogr. 41 (9), 1673–1682.Google Scholar
Holmes, R. M., Moum, J. N. & Thomas, L. N. 2016 Evidence for seafloor-intensified mixing by surface-generated equatorial waves. Geophys. Res. Lett. 43 (3), 1202–1210.CrossRefGoogle Scholar
Kunze, E. 1985 Near-inertial wave propagation in geostrophic shear. J. Phys. Oceanogr. 15 (5), 544–565.Google Scholar
MacKinnon, J. A. & Winters, K. B. 2005 Subtropical catastrophe: significant loss of low-mode tidal energy at 28. 9° . Geophys. Res. Lett. 32 (15), L15605+.Google Scholar
NCEP reanalyses 2016 Mid-latitude Northern Atlantic Ocean. http://rda.ucar.edu/datasets/ds094.1/.Google Scholar
Phillips, N. A. 1954 Energy transformations and meridional circulations associated with simple baroclinic waves in a two-level, quasi-geostrophic model. Tellus 6 (3), 273–286.Google Scholar
Pierrehumbert, R. T. & Swanson, K. L. 1995 Baroclinic instability. Annu. Rev. Fluid Mech. 27 (1), 419–467.Google Scholar
Roullet, G., McWilliams, J. C., Capet, X. & Molemaker, M. J. 2011 Properties of steady geostrophic turbulence with isopycnal outcropping. J. Phys. Oceanogr. 42 (1), 18–38.Google Scholar
Smith, K. S. 2007 The geography of linear baroclinic instability in Earth’s oceans. J. Mar. Res. 65 (5), 655–683.Google Scholar
Weller, R. A. 1982 The relation of near-inertial motions observed in the mixed layer during the Jasin (1978) experiment to the local wind stress and to the quasi-geostrophic flow field. J. Phys. Oceanogr. 12 (10), 1122–1136.Google Scholar
Winters, K. B. 2015 Tidally-forced flow in a rotating, stratified, shoaling basin. Ocean Model. 90, 72–81.Google Scholar
Winters, K. B., Bouruet-Aubertot, P. & Gerkema, T. 2011 Critical reflection and abyssal trapping of near-inertial waves on a 𝛽-plane. J. Fluid Mech. 684, 111–136.Google Scholar
Winters, K. B. & D’Asaro, E. A. 1997 Direct simulation of internal wave energy transfer. J. Phys. Oceanogr. 27 (9), 1937–1945.Google Scholar
Winters, K. B. & de la Fuente, A. 2012 Modelling rotating stratified flows at laboratory-scale using spectrally-based DNS. Ocean Model. 49–50, 47–59.Google Scholar
Winters, K. B., MacKinnon, J. A. & Mills, B. 2004 A spectral model for process studies of rotating, density-stratified flows. J. Atmos. Ocean. Technol. 21 (1), 69–94.Google Scholar