Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-20T01:05:37.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Phoretic self-propulsion at large Péclet numbers

Published online by Cambridge University Press:  27 February 2015

Ehud Yariv  and
Sébastien Michelin
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
Sébastien Michelin
Affiliation:
LadHyX, Département de Mécanique, Ecole Polytechnique – CNRS, 91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the self-diffusiophoresis of a spherical particle animated by a non-uniform chemical reaction at its boundary. We consider two models of solute absorption, one with a specified distribution of interfacial solute flux and one where this flux is governed by first-order kinetics with a specified distribution of rate constant. We employ a macroscale model where the short-range interaction of the solute with the particle boundary is represented by an effective slip condition. The solute transport is governed by an advection–diffusion equation. We focus upon the singular limit of large Péclet numbers, 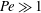$\mathit{Pe}\gg 1$. In the fixed-flux model, the excess-solute concentration is confined to a narrow boundary layer. The scaling pertinent to that limit allows the problem governing the solute concentration to be decoupled from the flow field. The resulting nonlinear boundary-layer problem is handled using a transformation to stream-function coordinates and a subsequent application of Fourier transforms, and is thereby reduced to a nonlinear integral equation governing the interfacial concentration. Its solution provides the requisite approximation for the particle velocity, which scales as 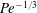$\mathit{Pe}^{-1/3}$. In the fixed-rate model, large Péclet numbers may be realized in different limit processes. We consider the case of large swimmers or strong reaction, where the Damköhler number 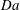$\mathit{Da}$ is large as well, scaling as 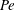$\mathit{Pe}$. In that double limit, where no boundary layer is formed, we obtain a closed-form approximation for the particle velocity, expressed as a nonlinear functional of the rate-constant distribution; this velocity scales as 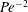$\mathit{Pe}^{-2}$. Both the fixed-flux and fixed-rate asymptotic predictions agree with the numerical values provided by computational solutions of the nonlinear transport problem.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 768 , 10 April 2015 , R1
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Chambré, P. L. 1957 Laminar boundary layer flows with surface reactions. Ind. Engng Chem. 49 (6), 1025–1029.CrossRefGoogle Scholar
Acrivos, A. & Goddard, J. D. 1965 Asymptotic expansions for laminar forced-convection heat and mass transfer. Part 1. Low speed flows. J. Fluid Mech. 23 (02), 273–291.CrossRefGoogle Scholar
Anderson, J. L., Lowell, M. E. & Prieve, D. C. 1982 Motion of a particle generated by chemical gradients. Part 1. Non-electrolytes. J. Fluid Mech. 117 (1), 107–121.CrossRefGoogle Scholar
Brady, J. F. 2011 Particle motion driven by solute gradients with application to autonomous motion: continuum and colloidal perspectives. J. Fluid Mech. 667, 216–259.CrossRefGoogle Scholar
Brenner, H. 1964 The Stokes resistance of an arbitrary particle – IV. Arbitrary fields of flow. Chem. Engng Sci. 19, 703–727.CrossRefGoogle Scholar
Córdova-Figueroa, U. M. & Brady, J. F. 2008 Osmotic propulsion: the osmotic motor. Phys. Rev. Lett. 100 (15), 158303.CrossRefGoogle ScholarPubMed
Golestanian, R., Liverpool, T. B. & Ajdari, A. 2007 Designing phoretic micro- and nano-swimmers. New J. Phys. 9, 126.CrossRefGoogle Scholar
Jülicher, F. & Prost, J. 2009a Comment on ‘Osmotic propulsion: the osmotic motor’. Phys. Rev. Lett. 103 (7), 079801.CrossRefGoogle ScholarPubMed
Jülicher, F. & Prost, J. 2009b Generic theory of colloidal transport. Eur. Phys. J. E 29 (1), 27–36.CrossRefGoogle ScholarPubMed
Levich, V. G. 1962 Physicochemical Hydrodynamics. Prentice-Hall.Google Scholar
Magar, V., Goto, T. & Pedley, T. J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Maths 56 (1), 65–91.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23, 101901.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2014 Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 747, 572–604.CrossRefGoogle Scholar
Moran, J. L., Wheat, P. M. & Posner, J. D. 2010 Locomotion of electrocatalytic nanomotors due to reaction induced charge auto-electrophoresis. Phys. Rev. E 81 (6), 65302.CrossRefGoogle Scholar
Saville, D. A. 1977 Electrokinetic effects with small particles. Annu. Rev. Fluid Mech. 9, 321–337.CrossRefGoogle Scholar
Schnitzer, O., Frankel, I. & Yariv, E. 2013 Electrokinetic flows about conducting drops. J. Fluid Mech. 722, 394–423.CrossRefGoogle Scholar
Schnitzer, O., Frankel, I. & Yariv, E. 2014 Electrophoresis of bubbles. J. Fluid Mech. 753, 49–79.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2012a Macroscale description of electrokinetic flows at large zeta potentials: nonlinear surface conduction. Phys. Rev. E 86, 021503.CrossRefGoogle ScholarPubMed
Schnitzer, O. & Yariv, E. 2012b Strong-field electrophoresis. J. Fluid Mech. 701, 333–351.CrossRefGoogle Scholar
Stone, H. A. & Samuel, A. D. T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77 (19), 4102.CrossRefGoogle ScholarPubMed
Yariv, E. 2009 An asymptotic derivation of the thin-Debye-layer limit for electrokinetic phenomena. Chem. Engng Commun. 197, 3–17.CrossRefGoogle Scholar
Yariv, E. 2011 Electrokinetic self-propulsion by inhomogeneous surface kinetics. Proc. R. Soc. Lond. A 467 (2130), 1645–1664.Google Scholar
Yariv, E., Schnitzer, O. & Frankel, I. 2011 Streaming-potential phenomena in the thin-Debye-layer limit. Part 1. General theory. J. Fluid Mech. 685, 306–334.CrossRefGoogle Scholar