Hostname: page-component-6587cd75c8-67gbf Total loading time: 0 Render date: 2025-04-24T03:59:10.062Z Has data issue: false hasContentIssue false
  • English
  • Français

Path instabilities of freely falling oblong cylinders

Published online by Cambridge University Press:  27 November 2024

G. Bouchet Open the ORCID record for G. Bouchet [Opens in a new window]  and
J. Dušek Open the ORCID record for J. Dušek [Opens in a new window]
G. Bouchet*
Affiliation:
Aix Marseille Univ, CNRS, IUSTI, Marseille, France
J. Dušek
Affiliation:
Université de Strasbourg, CNRS, ICube, Strasbourg, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

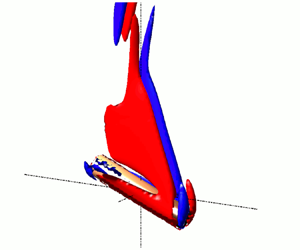
This paper presents numerical simulations of the free fall of homogenous cylinders of length-to-diameter ratios $2$, $3$ and 5 and solid-to-fluid-density ratios $\rho _s/\rho$ going from 0 to 10 in transitional regimes. The path instabilities are shown to be due to two types of transitional states. The well-known fluttering state is a solid mode, characterised by significant oscillations of the cylinder axis due to a strong interaction between the vortex shedding in the wake and the solid degrees of freedom. Weakly oscillating, mostly irregular trajectories, are fluid modes, associated with purely fluid instabilities in the wake. The interplay of solid and fluid modes leads to a varying scenario in which the length-to-diameter and density ratios play an important role. The description is accompanied by the presentation of the identified transitional states in terms of path characteristics and vorticity structure of the wakes and by bifurcation diagrams showing the evolution of asymptotic states with increasing Galileo numbers. There appears to be a strong difference between the behaviour of cylinders of aspect ratio $L/d=3$ and 5. A similar contrast is stated between light cylinders of density ratios $\rho _s/\rho \le 2$ and dense cylinders of density ratios 5 and 10. Finally, the question of the scatter of values of the drag coefficient and of the frequency of oscillations raised in the literature is addressed. It is shown, that in addition to external parameters (Galileo number, density and aspect ratio) the amplitude of oscillations characterising the instability development is to be taken into account to explain this scatter. Fits of the simulation results to simple correlations are proposed. Namely that of the drag coefficient proves to be accurate (better than 1 % of accuracy) but also that of the Strouhal number (a few per cent of accuracy) may be of practical use.

JFM classification

Instability: Nonlinear instability Multiphase and Particle-laden Flows: Particle/fluid flow Nonlinear Dynamical Systems: Bifurcation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A54
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Auguste, F., Magnaudet, J. & Fabre, D. 2013 Falling styles of discs. J. Fluid Mech. 719, 388–405.CrossRefGoogle Scholar
Blanco, M.A., Flórez, M. & Bermejo, M. 1997 Evaluation of the rotation matrices in the basis of real spherical harmonics. J. Mol. Struct. 419, 19–27.CrossRefGoogle Scholar
Chow, A.C. & Adams, E.E. 2011 Prediction of drag coefficient and secondary motion of freefalling rigid cylindrical particles with and without curvature at moderate Reynolds number. ASCE J. Hydraul. Engng 137, 1406–1414.CrossRefGoogle Scholar
Chrust, M. 2012 Etude numérique de la chute d'objets axisymétriques dans un fluide Newtonien. PhD thesis, Université de Strasbourg, in English at https://publication-theses.unistra.fr/public/theses_doctorat/2012/Chrust_Marcin_2012_ED269.pdf.Google Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25, 044102.CrossRefGoogle Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2014 Effect of solid body degrees of freedom on the path instabilities of freely falling or rising flat cylinders. J. Fluids Struct. 47, 55–70.CrossRefGoogle Scholar
Clift, R., Grace, J.R. & Weber, M.E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
Dušek, J., Zhou, W. & Chrust, M. 2021 Solid–fluid interaction in path instabilities of sedimenting flat objects. In Fluid–Structure-Sound Interactions and Control (ed. M. Braza, Y. Hoarau, Y. Zhou, A.D. Lucey, L. Huang & G.E. Stavroulakis), pp. 57–62. Springer.CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2011 Wake-induced oscillatory paths of bodies freely rising of falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fernandes, P.C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.CrossRefGoogle Scholar
Ghidersa, B. & Dušek, J. 2000 Breaking of axisymetry and onset of unsteadiness in the wake of a sphere. J. Fluid Mech. 423, 33–69.CrossRefGoogle Scholar
Hecht, K.T. 2000 Quantum Mechanics. Springer.CrossRefGoogle Scholar
Inoue, P. & Sakuragi, A. 2008 Vortex shedding from a circular cylinder of finite length at low Reynolds numbers. Phys. Fluids 20, 033601.CrossRefGoogle Scholar
Jayaweera, K.O.L.F. & Mason, B.J. 1965 The behaviour of freely falling cylinders and cones in a viscous fluid. J. Fluid Mech. 22, 709–720.CrossRefGoogle Scholar
Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
Johnson, T.A. & Patel, V.C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Lorite-Diez, M., Ern, P., Cazin, S., Mougel, J. & Bourguet, R. 2022 An experimental study of flow–structure interaction regimes of a freely falling flexible cylinder. J. Fluid Mech. 946, A16–35.CrossRefGoogle Scholar
Marchildon, E.K., Clamen, A. & Gauvin, W.H. 1964 Drag and oscillatory motion of freely falling cylindrical particles. Can. J. Chem. Engng 42, 178–182.CrossRefGoogle Scholar
Meliga, P., Chomaz, J.M. & Sipp, D. 2009 Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.CrossRefGoogle Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.CrossRefGoogle Scholar
Pierson, J.-L., Auguste, F., Hammouti, A. & Wachs, A. 2019 Inertial flow past a finite-length axisymmetric cylinder of aspect ratio 3: effect of the yaw angle. Phys. Rev. Fluids 4, 044802.CrossRefGoogle Scholar
Romero-Gomez, P. & Richmond, M.C. 2016 Numerical simulation of circular cylinders in free-fall. J. Fluids Struct. 61, 154–167.CrossRefGoogle Scholar
Tchoufag, J., Fabre, D. & Magnaudet, J. 2014 Global linear stability analysis of the wake and path of buoyancy-driven disks and thin cylinders. J. Fluid Mech. 740, 278–311.CrossRefGoogle Scholar
Toupoint, C., Ern, P. & Roig, V. 2019 Kinematics and wake of freely falling cylinders at moderate Reynolds numbers. J. Fluid Mech. 866, 82–111.CrossRefGoogle Scholar
Yasseri, S. 2014 Experiment of free-falling cylinders in water. Underwater Technol. 32, 177–191.CrossRefGoogle Scholar
Zhou, W., Chrust, M. & Dušek, J. 2017 Path instabilities of oblate spheroids. J. Fluid Mech. 833, 445–468.CrossRefGoogle Scholar
Zielinska, B.J.A., Goujon-Durand, S., Dušek, J. & Wesfreid, J.E. 1997 A strongly non linear effect in unstable wakes. Phys. Rev. Lett. 79, 3893–3896.CrossRefGoogle Scholar