Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T06:40:53.296Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle-laden flow down a slope in uniform stratification

Published online by Cambridge University Press:  14 August 2014

Kate Snow  and
B. R. Sutherland
Kate Snow
Affiliation:
Research School of Earth Sciences, Australian National University, Acton, ACT 0200, Australia ARC Centre of Excellence for Climate System Science, University of New South Wales, Sydney, NSW 2052, Australia
B. R. Sutherland*
Affiliation:
Department of Physics, University of Alberta, Edmonton, T6G 2E1, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Lock–release laboratory experiments are performed to examine saline and particle-laden flows down a slope into both constant-density and linearly stratified ambients. Both hypopycnal (surface-propagating) currents and hyperpycnal (turbidity) currents are examined, with the focus being upon the influence of ambient stratification on turbidity currents. Measurements are made of the along-slope front speed and the depth at which the turbidity current separates from the slope and intrudes into the ambient. These results are compared to the predictions of a theory that characterizes the flow evolution and separation depth in terms of the slope $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}s$, the entrainment parameter 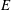$E$ (the ratio of entrainment to flow speed), the relative stratification parameter 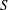$S$ (the ratio of the ambient density difference to the relative current density) and a new parameter 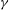$\gamma $ defined to be the ratio of the particle settling to entrainment speed. The implicit prediction for the separation depth, 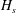$H_s$, is made explicit by considering limits of small and large separation depth. In the former case of a ‘weak’ turbidity current, entrainment and particle settling are unimportant and separation occurs where the density of the ambient fluid equals the density of the fluid in the lock. In the latter case of a ‘strong’ turbidity current, entrainment and particle settling crucially affect the separation depth. Consistent with theory, we find that the separation depth indeed depends on 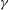$\gamma $ if the particle size (and hence settling rate) is sufficiently large and if the current propagates many lock lengths before separating from the slope. A composite prediction that combines the explicit formulae for the separation depth for weak and strong turbidity currents agrees well with experimental measurements over a wide parameter range.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 251 - 273
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antenucci, J. P., Ghadouami, A., Burford, M. A. & Romero, J. R. 2005 The long-term effect of artificial destratification on phytoplankton species composition in a subtropical reservoir. Freshwat. Biol. 50, 1081–1093.CrossRefGoogle Scholar
Baines, P. G. 2001 Mixing in flows down gentle slopes into stratified environments. J. Fluid Mech. 443, 237–270.Google Scholar
Baines, P. G. 2008 Mixing in flows down gentle slopes into stratified environments. Atmos.-Ocean 46, 405–419.CrossRefGoogle Scholar
Beghin, P., Hopfinger, E. J. & Britter, R. E. 1981 Gravitational convection from instantaneous sources on inclined boundaries. J. Fluid Mech. 107, 407–422.CrossRefGoogle Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Birman, V. K., Battandier, B. A., Meiburg, E. & Linden, P. F. 2007 Lock-exchange flow in slope channels. J. Fluid Mech. 577, 53–77.CrossRefGoogle Scholar
Bonnecaze, R. T., Huppert, H. E. & Lister, J. R. 1993 Particle-driven gravity currents. J. Fluid Mech. 250, 339–369.Google Scholar
Bonnecaze, R. T. & Lister, J. R. 1999 Particle-driven gravity currents down planar slopes. J. Fluid Mech. 390, 75–91.Google Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99, 531–543.Google Scholar
Bruschi, R., Bughi, S., Spinazzé, M., Torselletti, E. & Vitali, L. 2006 Impact of debris flows and turbidity currents on seafloor structures. Norw. J. Geol. 86, 317–336.Google Scholar
de Cesare, G., Boillat, J. L. & Schleiss, A. J. 2006 Circulation in stratified lakes due to flood-induced turbidity currents. J. Environ. Engng 132, 1508–1517.Google Scholar
Chung, S. W. & Gu, R. 1998 Two-dimensional simulations of contaminant currents in stratified reservoir. J. Hydraul. Engng 124, 704–711.Google Scholar
Cortés, A., Fleenor, W. E., Wells, M. G., de Vincente, I. & Rueda, F. J. 2014 Pathways of river water to the surface layers of stratified reservoirs. Limnol. Oceanogr. 59, 233–250.CrossRefGoogle Scholar
Fernandez, R. & Imberger, J. 2008 Time-varying underflow into a continuous stratification with bottom slope. J. Hydraul. Engng 134, 1191–1198.CrossRefGoogle Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.Google Scholar
Hogg, A. J., Huppert, H. E. & Hallworth, M. A. 1999 Reversing buoyancy of particle-driven gravity current. Phys. Fluids 11, 2891–2900.Google Scholar
Hogg, A. J., Huppert, H. E. & Hallworth, M. A. 2000 Particle-driven gravity currents: asymptotic and box model solutions. Eur. J. Mech. (B/Fluids) 19, 139–165.CrossRefGoogle Scholar
Hughes, G. O. & Griffiths, R. W. 2006 A simple convective model of the global overturning circulation, including effects of entrainment into sinking regions. Ocean Model. 12, 46–79.Google Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.CrossRefGoogle Scholar
Hurzeler, B. E., Ivey, G. N. & Imberger, J. 1995 Spreading model for a turbidity current with reversing buoyancy from a constant-volume release. Mar. Freshwat. Res. 46, 393–408.Google Scholar
Lawrence, A. A., McCaffrey, W. D. & Talling, P. J. 2009 Special issue introduction: Sediment gravity flows – recent insights into their dynamic and stratified/composite nature. Mar. Petrol. Geol. 26, 1897–1899.Google Scholar
Martin, D. & Nokes, R. 1989 A fluid-dynamics study of crystal settling in convecting magmas. J. Petrol. 30, 1471–1500.CrossRefGoogle Scholar
Masson, D. G., Arzola, R. G., Wynn, R. B., Hunt, J. E. & Weaver, P. P. E. 2011 Seismic triggering of landslides and turbidity currents offshore Portugal. Geochem. Geophys. Geosyst. 12, Q12011.CrossRefGoogle Scholar
Maxworthy, T., Leilich, J., Simpson, J. E. & Meiburg, E. H. 2002 The propagation of a gravity current into a linearly stratified fluid. J. Fluid Mech. 453, 371–394.Google Scholar
Monaghan, J. J., Cas, R. A. F., Kos, A. M. & Hallworth, M. 1999 Gravity currents descending a ramp in a stratified tank. J. Fluid Mech. 379, 39–69.Google Scholar
Mulder, T. & Syvitski, J. P. M. 1995 Gravity currents descending a ramp in a stratified tank. J. Geol. 103, 285–299.Google Scholar
Mulder, T., Syvitski, J. P. M., Migeon, S., Faugeres, J. C. & Savoye, B. 2003 Marine hyperpycnal flows: initiation, behaviour and related deposits. A review. Mar. Petrol. Geol. 20, 861–882.Google Scholar
Parson, J. P., Bush, J. W. M. & Syvitski, J. P. M. 2001 Hyperpycnal plume formation from riverine outflows with small sediment concentration. Sedimentology 48, 465–478.Google Scholar
Paull, C. K., Ussler, W. III, Greene, H. G., Keaten, R., Mitts, P. & Barry, J. 2003 Caught in the act: the 20 December 2001 gravity flow event in Monterey Canyon. Geo-Mar. Lett. 22, 227–232.Google Scholar
Rimoldi, B., Alexander, J. & Morris, S. 1996 Experimental turbidity currents entering density stratified water: analogues for turbidites in Mediterranean hypersaline basins. Sedimentology 43, 527–540.CrossRefGoogle Scholar
de Rooij, F.1999 Sedimenting particle-laden flows in confined geometries. PhD thesis, University of Cambridge.Google Scholar
de Rooij, F., Linden, P. F. & Dalziel, S. B. 1999 Saline and particle-driven interfacial intrusions. J. Fluid Mech. 389, 303–334.Google Scholar
Shepard, F. P., McLoughlin, P. A., Marshall, N. F. & Sullivan, G. G. 2013 Current-meter recordings of low-speed turbidity currents. Geology 5, 297–301.Google Scholar
Shin, J. O., Dalziel, S. B. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.CrossRefGoogle Scholar
Sparks, R. S. J., Bonnecaze, R. T., Huppert, H. E., Lister, J. R., Hallworth, M. A., Mader, H. & Phillips, J. 1993 Sediment-laden gravity currents with reversing buoyancy. Earth Planet. Sci. Lett. 114, 243–257.Google Scholar
Straub, K. M.2007 Quantifying turbidity current interaction with topography. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Thomson, R. E., Davis, E. E., Heesemann, M. & Villinger, H. 2010 Observations of long-duration episodic bottom currents in the Middle America Trench: evidence for tidally initiated turbidity flows. J. Geophys. Res. 115, C006166.Google Scholar
Tokyay, T. E. & Garcia, M. H. 2014 Effect of initial excess density and discharge on constant flux gravity currents propagating on a slope. Environ. Fluid Mech. 14, 409–429.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Ungarish, M. 2006 On gravity currents in a linearly stratified ambient: a generalization of Benjamin’s steady-state propagation results. J. Fluid Mech. 548, 49–68.CrossRefGoogle Scholar
Wells, M. & Nadarajah, P. 2009 The intrusion depth of density currents flowing into stratified water bodies. J. Phys. Oceanogr. 39, 1935–1947.Google Scholar

Snow and Sutherland supplementary movie

Movie corresponding to experiment shown in Figures 3, 4c and 5 of a turbidity current in a stratified ambient

Download Snow and Sutherland supplementary movie(Video)
Video 2.3 MB

Snow and Sutherland supplementary movie

Movie corresponding to experiment shown in Figure 4a of a saline gravity current in a uniform density ambient

Download Snow and Sutherland supplementary movie(Video)
Video 974.8 KB

Snow and Sutherland supplementary movie

Movie corresponding to experiment shown in Figure 4b of a turbidity current in a uniform density ambient

Download Snow and Sutherland supplementary movie(Video)
Video 1.6 MB

Snow and Sutherland supplementary movie

Movie corresponding to experiment shown in Figure 7 of a turbidity current in a stratified ambient that separates from the slope close to the lock.

Download Snow and Sutherland supplementary movie(Video)
Video 2.7 MB

Snow and Sutherland supplementary movie

Movie corresponding to experiment shown in Figure 8 of what starts out as a hypopycnal particle-bearing current in a uniform density ambient

Download Snow and Sutherland supplementary movie(Video)
Video 3.2 MB