Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-20T00:25:38.639Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle capture by a circular cylinder in the vortex-shedding regime

Published online by Cambridge University Press:  19 September 2013

Alexis Espinosa-Gayosso ,
Marco Ghisalberti ,
Gregory N. Ivey  and
Nicole L. Jones
Alexis Espinosa-Gayosso*
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia UWA Oceans Institute, University of Western Australia, Crawley, WA 6009, Australia
Marco Ghisalberti
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia
Gregory N. Ivey
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia UWA Oceans Institute, University of Western Australia, Crawley, WA 6009, Australia
Nicole L. Jones
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia UWA Oceans Institute, University of Western Australia, Crawley, WA 6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

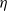Particle capture, whereby suspended particles contact and adhere to a solid surface (a ‘collector’), is an important mechanism for a range of environmental processes including suspension feeding by corals and ‘filtering’ by aquatic vegetation. In this paper, we use two- and three-dimensional direct numerical simulations to quantify the capture efficiency ($\eta $) of low-inertia particles by a circular cylindrical collector at intermediate Reynolds numbers in the vortex-shedding regime (i.e. for 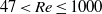$47\lt \mathit{Re}\leq 1000$, where 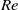$\mathit{Re}$ is the collector Reynolds number). We demonstrate that vortex shedding induces oscillations near the leading face of the collector which greatly affect the quantity and distribution of captured particles. Unlike in steady, low-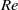$\mathit{Re}$ flow, particles directly upstream of the collector are not the most likely to be captured. Our results demonstrate the dependence of the time-averaged capture efficiency on 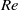$\mathit{Re}$ and particle size, improving the predictive capability for the capture of particles by aquatic collectors. The transition to theoretical high-Reynolds-number behaviour (i.e. 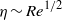$\eta \sim {\mathit{Re}}^{1/ 2} $) is complex due to comparatively rapid changes in wake conditions in this Reynolds number range.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Boundary Layers: Boundary layer structure
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 171 - 188
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ackerman, J. D. 2006 Sexual reproduction of seagrasses: pollination in the marine context. In Seagrasses: Biology, Ecology and Conservation (ed. Larkum, A. W. D., Orth, R. J. & Duarte, C. M.), Springer.Google Scholar
Bloor, M. S. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19 (2), 290–304.CrossRefGoogle Scholar
Bouhairie, S. & Chu, V. H. 2007 Two-dimensional simulation of unsteady heat transfer from a circular cylinder in crossflow. J. Fluid Mech. 570, 177–215.Google Scholar
Braza, M., Chassaing, P. & Minh, H. H. 1986 Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder. J. Fluid Mech. 165, 79–130.Google Scholar
Childs, E. P. & Mayle, R. E. 1984 Heat transfer on a rotationally oscillating cylinder in cross-flow. Intl J. Heat Mass Transfer 27 (1), 85–94.Google Scholar
Dwyer, H. A. & McCroskey, W. J. 1973 Oscillating flow over a cylinder at large Reynolds-number. J. Fluid Mech. 61 (4), 753–767.CrossRefGoogle Scholar
Espinosa-Gayosso, A., Ghisalberti, M., Ivey, G. N. & Jones, N. L. 2012 Particle capture and low-Reynolds-number flow around a circular cylinder. J. Fluid Mech. 710, 362–378.Google Scholar
Ferziger, J. H. & Peric, M. 2002 Computational Methods for Fluid Dynamics, 3rd edn. Springer.Google Scholar
Friedlander, S. K. 2000 Smoke, Dust and Haze. Fundamentals of Aerosol Dynamics, 2nd edn. Oxford University Press.Google Scholar
Glauert, M. B. 1956 The laminar boundary layer on oscillating plates and cylinders. J. Fluid Mech. 1 (1), 97–110.Google Scholar
Harvey, M., Bourget, E. & Ingram, R. G. 1995 Experimental evidence of passive accumulation of marine bivalve larvae on filamentous epibenthic structures. Limnol. Oceanogr. 40 (1), 94–104.Google Scholar
Haugen, N. E. L. & Kragset, S. 2010 Particle impaction on a cylinder in a crossflow as function of Stokes and Reynolds numbers. J. Fluid Mech. 661, 239–261.Google Scholar
Henderson, R. D. 1995 Details of the drag curve near the onset of vortex shedding. Phys. Fluids 7 (9), 2102–2104.CrossRefGoogle Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Hori, E.-I. 1962 Unsteady boundary layers, 3rd report, boundary layer on a circular cylinder in rotational oscillation. Bull. JSME 5 (17), 64–72.Google Scholar
Issa, R. I. 1986 Solution of the implicitly discretized fluid-flow equations by operator-splitting. J. Comput. Phys. 62 (1), 40–65.Google Scholar
Jordan, S. K. & Fromm, J. E. 1972 Oscillatory drag, lift, and torque on a circular cylinder in a uniform flow. Phys. Fluids 15 (3), 371–376.CrossRefGoogle Scholar
Lange, C. F., Durst, F. & Breuer, M. 1998 Momentum and heat transfer from cylinders in laminar crossflow at $1{0}^{- 4} \leq \mathit{Re}\leq 200$ . Intl J. Heat Mass Transfer 41 (22), 3409–3430.CrossRefGoogle Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.Google Scholar
Palmer, M. R., Nepf, H. M., Pettersson, T. J. R. & Ackerman, J. D. 2004 Observations of particle capture on a cylindrical collector: implications for particle accumulation and removal in aquatic systems. Limnol. Oceanogr. 49 (1), 76–85.Google Scholar
Parnas, R. & Friedlander, S. K. 1984 Particle deposition by diffusion and interception from boundary-layer flows. Aerosol Sci. Technol. 3 (1), 3–8.Google Scholar
Paxson, D. E. & Mayle, R. E. 1990 Velocity measurements on the forward portion of a cylinder. Trans. ASME J. Fluids Engng 112 (2), 243–245.Google Scholar
Phillips, C. G. & Kaye, S. R. 1999 The influence of the viscous boundary layer on the critical Stokes number for particle impaction near a stagnation point. J. Aerosol. Sci. 30 (6), 709–718.Google Scholar
Posdziech, O. & Grundmann, R. 2001 Numerical simulation of the flow around an infinitely long circular cylinder in the transition regime. Theor. Comput. Fluid Dyn. 15 (2), 121–141.Google Scholar
Posdziech, O. & Grundmann, R. 2007 A systematic approach to the numerical calculation of fundamental quantities of the two-dimensional flow over a circular cylinder. J. Fluids Struct. 23 (3), 479–499.Google Scholar
Schlichting, H. 1979 Boundary-layer Theory, 7th edn. McGraw-Hill.Google Scholar
Shimeta, J. & Koehl, M. A. R. 1997 Mechanisms of particle selection by tentaculate suspension feeders during encounter, retention, and handling. J. Expl Mar. Biol. Ecol. 209 (1–2), 47–73.Google Scholar
Watson, J. 1959 The two-dimensional liminar flow near the stagnation point of a cylinder which has an arbitrary transverse motion. Q. J. Mech. Appl. Maths 12 (2), 175–190.CrossRefGoogle Scholar
Weber, M. E. & Paddock, D. 1983 Interceptional and gravitational collision efficiencies for single collectors at intermediate Reynolds-numbers. J. Colloid Interface Sci. 94 (2), 328–335.Google Scholar
Wieselsberger, C. 1921 Neuere feststellungen über die gesetze des flüssigkeits- und luftwiderstands. Phys. Z. 22, 321–328.Google Scholar
Wildish, D. & Kristmanson, D. 1997 Benthic Suspension Feeders and Flow, 1st edn. Cambridge University Press.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, C. H. K. & Roshko, A. 1990 Measurements of base pressure in the wake of a cylinder at low Reynolds numbers. Z. Fluwiss. Weltraumforsch. 14 (1–2), 38–46.Google Scholar
Wu, M. H., Wen, C. Y., Yen, R. H., Weng, M. C. & Wang, A. B. 2004 Experimental and numerical study of the separation angle for flow around a circular cylinder at low Reynolds number. J. Fluid Mech. 515, 233–260.CrossRefGoogle Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders. Vol. 1: Fundamentals. Oxford University Press.CrossRefGoogle Scholar