Published online by Cambridge University Press: 18 February 2019
Parametric subharmonic instability arising in a narrow-band wave spectrum is investigated. Using a statistical equation that describes weakly nonlinear interactions in a random wave field, we perform analytical and numerical stability analyses for a modulating wave train. The analytically obtained growth rate 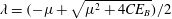 $\unicode[STIX]{x1D706}=(-\unicode[STIX]{x1D707}+\sqrt{\unicode[STIX]{x1D707}^{2}+4CE_{B}})/2$ agrees favourably with the results from direct numerical experiments, where
$\unicode[STIX]{x1D706}=(-\unicode[STIX]{x1D707}+\sqrt{\unicode[STIX]{x1D707}^{2}+4CE_{B}})/2$ agrees favourably with the results from direct numerical experiments, where 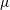 $\unicode[STIX]{x1D707}$ is the half-value width of the background wave frequency spectrum,
$\unicode[STIX]{x1D707}$ is the half-value width of the background wave frequency spectrum, 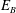 $E_{B}$ is the background wave energy density, and
$E_{B}$ is the background wave energy density, and 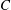 $C$ is a constant. This expression has two asymptotic limits:
$C$ is a constant. This expression has two asymptotic limits: 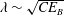 $\unicode[STIX]{x1D706}\sim \sqrt{CE_{B}}$ for
$\unicode[STIX]{x1D706}\sim \sqrt{CE_{B}}$ for 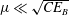 $\unicode[STIX]{x1D707}\ll \sqrt{CE_{B}}$ and
$\unicode[STIX]{x1D707}\ll \sqrt{CE_{B}}$ and  $\unicode[STIX]{x1D706}\sim CE_{B}/\unicode[STIX]{x1D707}$ for
$\unicode[STIX]{x1D706}\sim CE_{B}/\unicode[STIX]{x1D707}$ for 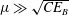 $\unicode[STIX]{x1D707}\gg \sqrt{CE_{B}}$. In the terms of weak turbulence, these two growth rates correspond to the ones occurring in the dynamic and kinetic time scales. In this way, our formulation successfully unifies the two conventional types of parametric subharmonic instability and offers a new criterion to determine the applicability of the classical kinetic equation in three-wave systems.
$\unicode[STIX]{x1D707}\gg \sqrt{CE_{B}}$. In the terms of weak turbulence, these two growth rates correspond to the ones occurring in the dynamic and kinetic time scales. In this way, our formulation successfully unifies the two conventional types of parametric subharmonic instability and offers a new criterion to determine the applicability of the classical kinetic equation in three-wave systems.