Published online by Cambridge University Press: 13 December 2016
Previous studies have predicted 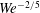 $We^{-2/5}$ dependence of the streamwise location at which primary breakup of turbulent liquid jets begins and
$We^{-2/5}$ dependence of the streamwise location at which primary breakup of turbulent liquid jets begins and 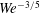 $We^{-3/5}$ dependence of the Sauter mean diameter (SMD) of droplets released at that location, where
$We^{-3/5}$ dependence of the Sauter mean diameter (SMD) of droplets released at that location, where 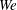 $We$ is the jet Weber number. Measured deviations from these predictions were attributed to measurement uncertainties and to the simplicity of the analysis, which invoked turbulence inertial-range phenomenology. Here, it is proposed that breakup onset is instead controlled by the residual presence of the boundary-layer structure of the nozzle flow in the near field of the jet. Assuming that the size of the breakup-inducing eddy is within the scale range of the log-law region,
$We$ is the jet Weber number. Measured deviations from these predictions were attributed to measurement uncertainties and to the simplicity of the analysis, which invoked turbulence inertial-range phenomenology. Here, it is proposed that breakup onset is instead controlled by the residual presence of the boundary-layer structure of the nozzle flow in the near field of the jet. Assuming that the size of the breakup-inducing eddy is within the scale range of the log-law region, 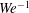 $We^{-1}$ dependence of both the onset location and the SMD at onset is predicted. These dependences agree with the available measurements more closely than those previously predicted. To predict the dependences on the Reynolds number
$We^{-1}$ dependence of both the onset location and the SMD at onset is predicted. These dependences agree with the available measurements more closely than those previously predicted. To predict the dependences on the Reynolds number 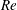 $Re$, either the friction velocity in conjunction with the Blasius friction law or the bulk velocity can be used, where the former yields
$Re$, either the friction velocity in conjunction with the Blasius friction law or the bulk velocity can be used, where the former yields 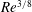 $Re^{3/8}$ and
$Re^{3/8}$ and 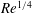 $Re^{1/4}$ dependence of the onset location and the SMD at onset respectively, while the latter implies no
$Re^{1/4}$ dependence of the onset location and the SMD at onset respectively, while the latter implies no 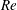 $Re$ dependence of either. The latter result is consistent with the available measurements, but the boundary-layer analysis indicates that the velocity scaling should be based on the friction velocity rather than the bulk velocity, so the origin of the measured lack of
$Re$ dependence of either. The latter result is consistent with the available measurements, but the boundary-layer analysis indicates that the velocity scaling should be based on the friction velocity rather than the bulk velocity, so the origin of the measured lack of 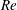 $Re$ dependence merits further investigation. A plausible hypothesis is that pressure effects associated with the transition from wall-bounded nozzle flow to jet free-slip boundary conditions induce a transient large-scale flow modification that counteracts the
$Re$ dependence merits further investigation. A plausible hypothesis is that pressure effects associated with the transition from wall-bounded nozzle flow to jet free-slip boundary conditions induce a transient large-scale flow modification that counteracts the 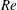 $Re$ dependence of the nozzle flow while preserving the logarithmic flow structure near the jet surface. Notwithstanding the absence of direct evidence supporting this hypothesis, the new analysis and comparisons of its predictions with measurements suggest that transient effects such as the residual influence of the nozzle-flow structure are the likely explanations of the observed parameter dependences.
$Re$ dependence of the nozzle flow while preserving the logarithmic flow structure near the jet surface. Notwithstanding the absence of direct evidence supporting this hypothesis, the new analysis and comparisons of its predictions with measurements suggest that transient effects such as the residual influence of the nozzle-flow structure are the likely explanations of the observed parameter dependences.