Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T14:50:30.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillatory and steady streaming flow in the anterior chamber of the moving eye

Published online by Cambridge University Press:  28 January 2019

M. Dvoriashyna Open the ORCID record for M. Dvoriashyna [Opens in a new window] ,
R. Repetto Open the ORCID record for R. Repetto [Opens in a new window]  and
J. H. Tweedy Open the ORCID record for J. H. Tweedy [Opens in a new window]
M. Dvoriashyna*
Affiliation:
Department of Civil, Chemical and Environmental Engineering, University of Genoa, Via Montallegro 1, Genoa 16145, Italy
R. Repetto
Affiliation:
Department of Civil, Chemical and Environmental Engineering, University of Genoa, Via Montallegro 1, Genoa 16145, Italy
J. H. Tweedy
Affiliation:
Department of Bioengineering, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the flow induced by eye rotations in the anterior chamber (AC) of the eye, the region between the cornea and the iris. We model the geometry of the AC as a thin domain sitting on the surface of a sphere, and study both the simpler case of a constant-height domain as well as a more realistic AC shape. We model eye rotations as harmonic in time with prescribed frequency 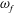$\unicode[STIX]{x1D714}_{f}$ and amplitude 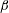$\unicode[STIX]{x1D6FD}$, and use lubrication theory to simplify the governing equations. We write the equations in a reference frame moving with the domain and show that fluid motion is governed by three dimensionless parameters: the aspect ratio $\unicode[STIX]{x1D716}$ of the AC, the angular amplitude 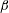$\unicode[STIX]{x1D6FD}$ and the Womersley number $\unicode[STIX]{x1D6FC}$. We simplify the equations under the physiologically realistic assumptions that $\unicode[STIX]{x1D716}$ is small and $\unicode[STIX]{x1D6FC}$ large, leading to a linear system that can be decomposed into three harmonics: a dominant frequency component, with frequency 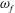$\unicode[STIX]{x1D714}_{f}$, and a steady streaming component and a third component with frequency 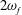$2\unicode[STIX]{x1D714}_{f}$. We solve the problem analytically for the constant-height domain and numerically as the solution of ordinary differential equations in the more realistic geometry. Both the primary flow and the steady streaming are shown to have a highly three-dimensional structure, which has not been highlighted in previous numerical works. We show that the steady streaming is particularly relevant from the clinical point of view, as it induces fluid mixing in the AC. Furthermore, the steady flow component is the dominant mixing mechanism during the night, when the thermal flow induced by temperature variations across the AC is suppressed.

JFM classification

Biological Fluid Dynamics: Biomedical flows Biological Fluid Dynamics: Biological Fluid Dynamics Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 904 - 926
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abouali, O., Modareszadeh, A., Ghaffarieh, A. & Tu, J. 2012 Investigation of saccadic eye movement effects on the fluid dynamic in the anterior chamber. J. Biomech. Engng 134 (2), 021002.10.1115/1.4005762Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Becker, W. 1989 Metrics. In The Neurobiology of Saccadic Eye Movements (ed. Wurtz, R. H. & Goldberg, M. E.), pp. 13–67. Elsevier Science.Google Scholar
Beswick, J. A. & McCulloch, C. 1956 Effect of hyaluronidase on the viscosity of the aqueous humour. Brit. J. Ophthalmol. 40 (9), 545–548.10.1136/bjo.40.9.545Google Scholar
Blondeaux, P. & Vittori, G. 1994 Wall imperfections as a triggering mechanism for Stokes-layer transition. J. Fluid Mech. 264, 107–135.10.1017/S0022112094000601Google Scholar
Bonfiglio, A., Lagazzo, A., Repetto, R. & Stocchino, A. 2015 An experimental model of vitreous motion induced by eye rotations. Eye Vis. 2 (1), 1–10.10.1186/s40662-015-0020-8Google Scholar
Bonfiglio, A., Repetto, R., Siggers, J. H. & Stocchino, A. 2013 Investigation of the motion of a viscous fluid in the vitreous cavity induced by eye rotations and implications for drug delivery. Phys. Med. Biol. 58 (6), 1969–1982.10.1088/0031-9155/58/6/1969Google Scholar
Boushehrian, H. H., Abouali, O., Jafarpur, K., Ghaffarieh, A. & Ahmadi, G. 2016 Relationship between saccadic eye movements and formation of the Krukenberg’s spindle: a CFD study. Math. Med. Biol. 34 (3), 293–312.Google Scholar
Brubaker, R. F. 1991 Flow of aqueous humor in humans [The Friedenwald Lecture]. Invest. Ophthalmol. Vis. Sci. 32 (13), 3145–3166.Google Scholar
Canning, C. R., Greaney, M. J., Dewynne, J. N. & Fitt, A. 2002 Fluid flow in the anterior chamber of a human eye. IMA J. Math. Appl. Med. Biol. 19, 31–60.10.1093/imammb/19.1.31Google Scholar
Colombini, M. 2014 Axisymmetric flow within a torsionally oscillating sphere. Phys. Fluids 26 (2), 023602.10.1063/1.4866812Google Scholar
David, T., Smye, S., Dabbs, T. & James, T. 1998 A model for the fluid motion of vitreous humour of the human eye during saccadic movement. Phys. Med. Biol. 43, 1385–1399.10.1088/0031-9155/43/6/001Google Scholar
Dvoriashyna, M., Repetto, R., Romano, M. R. & Tweedy, J. H. 2017 Aqueous humour flow in the posterior chamber of the eye and its modifications due to pupillary block and iridotomy. Math. Med. Biol. https://doi.org/10.1093/imammb/dqx012.Google Scholar
Fitt, A. D. & Gonzalez, G. 2006 Fluid mechanics of the human eye: aqueous humour flow in the anterior chamber. Bull. Math. Biol. 68 (1), 53–71.10.1007/s11538-005-9015-2Google Scholar
Friedland, A. B. 1978 A hydrodynamic model of aqueous flow in the posterior chamber of the eye. Bull. Math. Biol. 40, 223–235.10.1007/BF02461437Google Scholar
Helmholtz, H. 1909 Handbuch der physiologischen Optik, 3rd edn. University of Michigan Library.Google Scholar
Heys, J. J. & Barocas, V. H. 2002 A Boussinesq model of natural convection in the human eye and formation of Krunberg’s spindle. Ann. Biomed. Engng 30, 392–401.10.1114/1.1477447Google Scholar
Jivrajka, R., Shammas, M. C., Boenzi, T., Swearingen, M. & Shammas, H. J. 2008 Variability of axial length, anterior chamber depth, and lens thickness in the cataractous eye. J. Cataract Refract. Surg. 34 (2), 289–294.10.1016/j.jcrs.2007.10.015Google Scholar
Kaji, Y., Oshika, T., Usui, T. & Sakakibara, J. 2005 Effect of shear stress on attachment of corneal endothelial cells in association with corneal endothelial cell loss after laser iridotomy. Cornea 24 (8), S55–S58.10.1097/01.ico.0000178735.27674.52Google Scholar
Lide, D. R.(Ed.) 1996 CRC Handbook of Chemistry and Physics, 77th edn. CRC Press.Google Scholar
Maurice, D. M. 1998 The von Sallmann lecture 1996: an ophthalmological explanation of REM sleep. Exp. Eye Res. 66 (2), 139–145.10.1006/exer.1997.0444Google Scholar
Meskauskas, J., Repetto, R. & Siggers, J. H. 2011 Oscillatory motion of a viscoelastic fluid within a spherical cavity. J. Fluid Mech. 685, 1–22.10.1017/jfm.2011.263Google Scholar
Meskauskas, J., Repetto, R. & Siggers, J. H. 2012 Shape change of the vitreous chamber influences retinal detachment and reattachment processes: is mechanical stress during eye rotations a factor? Invest. Ophthalmol. Visual Sci. 53 (10), 6271–6281.10.1167/iovs.11-9390Google Scholar
Modarreszadeh, S., Abouali, O., Ghaffarieh, A. & Ahmadi, G. 2014 Physiology of aqueous humor dynamic in the anterior chamber due to rapid eye movement. Physiol. Behav. 135, 112–118.10.1016/j.physbeh.2014.05.017Google Scholar
Repetto, R., Pralits, J. O., Siggers, J. H. & Soleri, P. 2015 Phakic iris-fixated intraocular lens placement in the anterior chamber: effects on aqueous flow. Invest. Ophthalmol. Visual Sci. 56 (5), 3061–3068.10.1167/iovs.14-16118Google Scholar
Repetto, R., Siggers, J. H. & Stocchino, A. 2008 Steady streaming within a periodically rotating sphere. J. Fluid Mech. 608, 71–80.10.1017/S002211200800222XGoogle Scholar
Repetto, R., Siggers, J. H. & Stocchino, A. 2010 Mathematical model of flow in the vitreous humor induced by saccadic eye rotations: effect of geometry. Biomech. Model. Mechanobiol. 9 (1), 65–76.10.1007/s10237-009-0159-0Google Scholar
Repetto, R., Stocchino, A. & Cafferata, C. 2005 Experimental investigation of vitreous humour motion within a human eye model. Phys. Med. Biol. 50, 4729–4743.10.1088/0031-9155/50/19/021Google Scholar
Silver, D. M. & Quigley, H. A. 2004 Aqueous flow through the iris-lens channel: estimates of the differential pressure between the anterior and the posterior chambers. J. Glaucoma 13 (2), 100–107.10.1097/00061198-200404000-00004Google Scholar
Sommer, A., Tielsch, J. M., Katz, J., Quigley, H. A., Gottsch, J. D., Javitt, J. & Singh, K. 1991 Relationship between intraocular pressure and primary open angle glaucoma among white and black Americans. Arch. Ophthalmol. 109 (8), 1090–1095.10.1001/archopht.1991.01080080050026Google Scholar
Takahashi, K. & Atsumi, Y. 1997 Precise measurement of individual rapid eye movements in REM sleep of humans. Sleep 20 (9), 743–752.10.1093/sleep/20.9.743Google Scholar
Tweedy, J. H., Pralits, J. O., Repetto, R. & Soleri, P. 2017 Flow in the anterior chamber of the eye with an implanted iris-fixated artificial lens. Math. Med. Biol. 35 (3), 363–385.10.1093/imammb/dqx007Google Scholar
Urtti, A. 2006 Challenges and obstacles of ocular pharmacokinetics and drug delivery. Adv. Drug Deliv. Rev. 58 (11), 1131–1135.10.1016/j.addr.2006.07.027Google Scholar
Villamarin, A., Roy, S., Hasballa, R., Vardoulis, O., Reymond, P. & Stergiopulos, N. 2012 3D simulation of the aqueous flow in the human eye. Med. Engng Phys. 34, 1462–1470.10.1016/j.medengphy.2012.02.007Google Scholar