Published online by Cambridge University Press: 06 January 2020
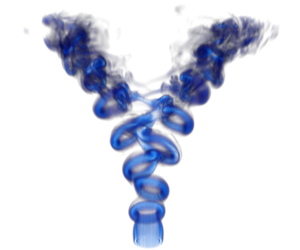
The present article aims at optimising the spread of a bifurcating jet: a jet that combines axisymmetric and helical forcing to achieve increased mixing in a preferential plane. Parekh et al. (Tech. Rep. TF-35, Stanford University, 1988) explained such a bifurcation as the result of nonlinear interaction between ring vortices (triggered by  $m=0$ axisymmetric forcing), shifted off-axis in alternate directions (owing to
$m=0$ axisymmetric forcing), shifted off-axis in alternate directions (owing to  $m=1$ helical forcing). Following this idea, we linearly optimise the periodic helical forcing to be applied at the inlet, in order to maximally displace the ring vortices of an axisymmetrically forced jet. Two norms are introduced for evaluating the effect of helical forcing onto the helical response: the standard
$m=1$ helical forcing). Following this idea, we linearly optimise the periodic helical forcing to be applied at the inlet, in order to maximally displace the ring vortices of an axisymmetrically forced jet. Two norms are introduced for evaluating the effect of helical forcing onto the helical response: the standard  ${\mathcal{L}}_{2}$-norm and a semi-norm reflecting the off-axis vortex displacement. The linear results show one dominant forcing mode over the entire Strouhal band studied (
${\mathcal{L}}_{2}$-norm and a semi-norm reflecting the off-axis vortex displacement. The linear results show one dominant forcing mode over the entire Strouhal band studied ( $0.35\leqslant St\leqslant 0.8$), with a large gain separation from suboptimals. The dominant forcing is mainly radial, independent of the chosen response norm, and provides a gain at least five times larger than what was achieved by previous ad hoc forcing strategies. Superposition of base flow and linear results show the alternate shifting and twisting provoked by the the small-amplitude helical forcing, which is an essential ingredient for triggering jet bifurcation. When tested in three-dimensional direct numerical simulations, low-amplitude helical forcing achieves efficient bifurcation at all Strouhal values studied. At high Strouhal numbers, an additional central branch emerges in the mean flow, leading to trifurcation. Across all frequencies, compared with ad hoc forcing strategies, the optimal forcing triggers a much stronger and robust spreading, by moving the bifurcation point upstream. As a result, bifurcating jets are observed over a much larger Strouhal band (
$0.35\leqslant St\leqslant 0.8$), with a large gain separation from suboptimals. The dominant forcing is mainly radial, independent of the chosen response norm, and provides a gain at least five times larger than what was achieved by previous ad hoc forcing strategies. Superposition of base flow and linear results show the alternate shifting and twisting provoked by the the small-amplitude helical forcing, which is an essential ingredient for triggering jet bifurcation. When tested in three-dimensional direct numerical simulations, low-amplitude helical forcing achieves efficient bifurcation at all Strouhal values studied. At high Strouhal numbers, an additional central branch emerges in the mean flow, leading to trifurcation. Across all frequencies, compared with ad hoc forcing strategies, the optimal forcing triggers a much stronger and robust spreading, by moving the bifurcation point upstream. As a result, bifurcating jets are observed over a much larger Strouhal band ( $0.35\leqslant St\leqslant 0.8$) compared with the band where ad hoc forcing achieves bifurcation in our setting (
$0.35\leqslant St\leqslant 0.8$) compared with the band where ad hoc forcing achieves bifurcation in our setting ( $0.4\leqslant St\leqslant 0.5$).
$0.4\leqslant St\leqslant 0.5$).