Article contents
Optimal transient growth in thin-interface internal solitary waves
Published online by Cambridge University Press: 12 February 2018
Abstract
The dynamics of perturbations to large-amplitude internal solitary waves (ISWs) in two-layered flows with thin interfaces is analysed by means of linear optimal transient growth methods. Optimal perturbations are computed through direct–adjoint iterations of the Navier–Stokes equations linearized around inviscid, steady ISWs obtained from the Dubreil-Jacotin–Long (DJL) equation. Optimal perturbations are found as a function of the ISW phase velocity  $c$ (alternatively amplitude) for one representative stratification. These disturbances are found to be localized wave-like packets that originate just upstream of the ISW self-induced zone (for large enough
$c$ (alternatively amplitude) for one representative stratification. These disturbances are found to be localized wave-like packets that originate just upstream of the ISW self-induced zone (for large enough  $c$) of potentially unstable Richardson number,
$c$) of potentially unstable Richardson number, 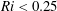 $Ri<0.25$. They propagate through the base wave as coherent packets whose total energy gain increases rapidly with
$Ri<0.25$. They propagate through the base wave as coherent packets whose total energy gain increases rapidly with  $c$. The optimal disturbances are also shown to be relevant to DJL solitary waves that have been modified by viscosity representative of laboratory experiments. The optimal disturbances are compared to the local Wentzel–Kramers–Brillouin (WKB) approximation for spatially growing Kelvin–Helmholtz (K–H) waves through the
$c$. The optimal disturbances are also shown to be relevant to DJL solitary waves that have been modified by viscosity representative of laboratory experiments. The optimal disturbances are compared to the local Wentzel–Kramers–Brillouin (WKB) approximation for spatially growing Kelvin–Helmholtz (K–H) waves through the 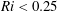 $Ri<0.25$ zone. The WKB approach is able to capture properties (e.g. carrier frequency, wavenumber and energy gain) of the optimal disturbances except for an initial phase of non-normal growth due to the Orr mechanism. The non-normal growth can be a substantial portion of the total gain, especially for ISWs that are weakly unstable to K–H waves. The linear evolution of Gaussian packets of linear free waves with the same carrier frequency as the optimal disturbances is shown to result in less energy gain than found for either the optimal perturbations or the WKB approximation due to non-normal effects that cause absorption of disturbance energy into the leading face of the wave. Two-dimensional numerical calculations of the nonlinear evolution of optimal disturbance packets leads to the generation of large-amplitude K–H billows that can emerge on the leading face of the wave and that break down into turbulence in the lee of the wave. The nonlinear calculations are used to derive a slowly varying model of ISW decay due to repeated encounters with optimal or free wave packets. Field observations of unstable ISW by Moum et al. (J. Phys. Oceanogr., vol. 33 (10), 2003, pp. 2093–2112) are consistent with excitation by optimal disturbances.
$Ri<0.25$ zone. The WKB approach is able to capture properties (e.g. carrier frequency, wavenumber and energy gain) of the optimal disturbances except for an initial phase of non-normal growth due to the Orr mechanism. The non-normal growth can be a substantial portion of the total gain, especially for ISWs that are weakly unstable to K–H waves. The linear evolution of Gaussian packets of linear free waves with the same carrier frequency as the optimal disturbances is shown to result in less energy gain than found for either the optimal perturbations or the WKB approximation due to non-normal effects that cause absorption of disturbance energy into the leading face of the wave. Two-dimensional numerical calculations of the nonlinear evolution of optimal disturbance packets leads to the generation of large-amplitude K–H billows that can emerge on the leading face of the wave and that break down into turbulence in the lee of the wave. The nonlinear calculations are used to derive a slowly varying model of ISW decay due to repeated encounters with optimal or free wave packets. Field observations of unstable ISW by Moum et al. (J. Phys. Oceanogr., vol. 33 (10), 2003, pp. 2093–2112) are consistent with excitation by optimal disturbances.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 7
- Cited by



