Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T07:52:41.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal streaks in the circular cylinder wake and suppression of the global instability

Published online by Cambridge University Press:  10 July 2014

Gerardo Del Guercio ,
Carlo Cossu Open the ORCID record for Carlo Cossu [Opens in a new window]  and
Gregory Pujals
Gerardo Del Guercio
Affiliation:
CNRS – Institut de Mécanique des Fluides de Toulouse (IMFT), Allée du Pr. Camille Soula, F-31400 Toulouse, France PSA Peugeot Citroën, Centre Technique de Velizy, 2 Route de Gisy, 78943 Vélizy-Villacoublay CEDEX, France
Carlo Cossu*
Affiliation:
CNRS – Institut de Mécanique des Fluides de Toulouse (IMFT), Allée du Pr. Camille Soula, F-31400 Toulouse, France
Gregory Pujals
Affiliation:
PSA Peugeot Citroën, Centre Technique de Velizy, 2 Route de Gisy, 78943 Vélizy-Villacoublay CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The steady, spanwise-periodic, symmetric (varicose) optimal blowing and suction that maximizes energy amplification in the circular cylinder wake is computed at Reynolds numbers ranging from 50 to 100. It is found that the cylinder wake can sustain large energy amplifications that are associated with the generation by the optimal blowing and suction of streamwise vortices near the cylinder, which then induce the transient spatial growth of high-energy streamwise streaks further downstream. The most amplified perturbations have spanwise wavelengths ranging from five to seven times the cylinder diameter at the Reynolds numbers considered, with the corresponding optimal streaks reaching their maximum amplitude in the near wake, inside the pocket of absolute instability which sustains the global instability. The optimal blowing and suction is shown to stabilize the global linear instability. The most stabilizing spanwise wavelengths are in good agreement with previous findings. The amplitude of optimal blowing and suction required to suppress the global instability decreases when the Reynolds number 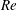$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}$ is increased from 75 to 100. This trend reveals the key role played by the non-normal amplification of the streaks in the stabilization process, which is able to overcome the increase of the uncontrolled global growth rate with 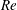$\mathit{Re}$. Finally, it is shown that the global instability can be suppressed with control amplitudes smaller than those required by 2-D (spanwise-uniform) control. This result is not what would be expected from first-order sensitivity analyses, which predict a zero sensitivity of the global instability to spanwise-periodic control and, in general, a non-zero sensitivity to spanwise-uniform control.

JFM classification

Instability: Absolute/convective instability Flow Control: Instability control Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 572 - 588
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdessemed, N., Sharma, A. S., Sherwin, S. J. & Theofilis, V. 2009 Transient growth analysis of the flow past a circular cylinder. Phys. Fluids 21, 044103.CrossRefGoogle Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.CrossRefGoogle Scholar
Bearman, P. W. & Owen, J. C. 1998 Reduction of bluff-body drag and suppression of vortex shedding by the introduction of wavy separation lines. J. Fluids Struct. 12 (1), 123–130.CrossRefGoogle Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.CrossRefGoogle Scholar
Choi, H., Jeon, W. P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
Chomaz, J. M. 2005 Global instabilities in spatially developing flows: nonnormality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1988 Bifurcations to local and global modes in spatially developing flows. Phys. Rev. Lett. 60, 25–28.CrossRefGoogle ScholarPubMed
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14, L57–L60.CrossRefGoogle Scholar
Cossu, C. & Brandt, L. 2004 On Tollmien–Schlichting waves in streaky boundary layers. Eur. J. Mech. (B/Fluids) 23, 815–833.CrossRefGoogle Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.CrossRefGoogle Scholar
Darekar, R. M. & Sherwin, S. J. 2001 Flow past a square-section cylinder with a wavy stagnation face. J. Fluid Mech. 426 (1), 263–295.CrossRefGoogle Scholar
Dennis, S. C. R. & Chang, G. Z. 1970 Numerical solutions for steady flow past a circular cylinder at Reynolds numbers up to 100. J. Fluid Mech. 42, 471–489.CrossRefGoogle Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.CrossRefGoogle Scholar
Fornberg, B. 1980 A numerical study of steady viscous flow past a circular cylinder. J. Fluid Mech. 98, 819–855.CrossRefGoogle Scholar
Fransson, J., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilisation of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17, 054110.CrossRefGoogle Scholar
Fransson, J., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96, 064501.CrossRefGoogle ScholarPubMed
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Del Guercio, G., Cossu, C. & Pujals, G. 2014a Stabilizing effect of optimally amplified streaks in parallel wakes. J. Fluid Mech. 739, 37–56.CrossRefGoogle Scholar
Del Guercio, G., Cossu, C. & Pujals, G. 2014b Optimal perturbations of non-parallel wakes and their stabilizing effect on the global instability. Phys. Fluids 26, 024110.CrossRefGoogle Scholar
Gustavsson, L. H. 1991 Energy growth of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 224, 241–260.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Hwang, Y., Kim, J. & Choi, H. 2013 Stabilization of absolute instability in spanwise wavy two-dimensional wakes. J. Fluid Mech. 727, 346–378.CrossRefGoogle Scholar
Kachanov, Y. S. & Tararykin, O. I. 1987 Experimental investigation of a relaxing boundary layer. Izv. Sib. Otd. An. Tech. 18, 9–19.Google Scholar
Kim, J. & Choi, H. 2005 Distributed forcing of flow over a circular cylinder. Phys. Fluids 17, 033103.CrossRefGoogle Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.CrossRefGoogle Scholar
Moffatt, H. K. 1967 The interaction of turbulence with strong wind shear. In Proceedings of the URSI-IUGG International Colloquium on Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 139–154. Nauka.Google Scholar
Monkewitz, P. A. 1988 The absolute and convective nature of instability in two-dimensional wakes at low Reynolds numbers. Phys. Fluids 31, 999–1006.CrossRefGoogle Scholar
Pujals, G., Cossu, C. & Depardon, S. 2010a Forcing large-scale coherent streaks in a zero pressure gradient turbulent boundary layer. J. Turbul. 11 (25), 1–13.CrossRefGoogle Scholar
Pujals, G., Depardon, S. & Cossu, C. 2010b Drag reduction of a 3-D bluff body using coherent streamwise streaks. Exp. Fluids 49 (5), 1085–1094.CrossRefGoogle Scholar
Tanner, M. 1972 A method of reducing the base drag of wings with blunt trailing edges. Aeronaut. Q. 23, 15–23.CrossRefGoogle Scholar
Tombazis, N. & Bearman, P. W. 1997 A study of three-dimensional aspects of vortex shedding from a bluff body with a mild geometric disturbance. J. Fluid Mech. 330, 85–112.CrossRefGoogle Scholar