Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T08:34:05.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal perturbations of gravitationally unstable, transient boundary layers in porous media

Published online by Cambridge University Press:  27 June 2013

Don Daniel ,
Nils Tilton  and
Amir Riaz
Don Daniel
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
Nils Tilton
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
Amir Riaz*
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

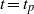We study the linear stability of gravitationally unstable, transient, diffusive boundary layers in porous media using non-modal stability theory. We first perform a classical optimization procedure, using an adjoint-based method, to obtain the perturbations at the initial time $t= {t}_{p} $ that have a maximum amplification at a final time 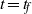$t= {t}_{f} $. We then investigate the sensitivity of the optimal perturbations to the initial time, 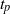${t}_{p} $, and the final time, 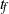${t}_{f} $, as well as different measures of perturbation amplification. Due to the transient nature of the base state, we demonstrate that there is an optimal initial perturbation time, 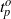${ t}_{p}^{o} $. By rescaling the problem, we develop analytical relationships for the optimal initial time and wavenumber in terms of aquifer properties. We also demonstrate that the classical optimization procedure essentially recovers the dominant perturbation structures predicted by a quasi-steady modal analysis. Although the classical optimal perturbations are mathematically valid, we observe that due to physical constraints, they are unlikely to reflect analogous laboratory experiments. Therefore, we propose a modified optimization procedure (MOP) that constrains the optimization to physically admissible initial perturbation fields. We compare the results of the classical and modified optimization procedures with quasi-steady modal analyses and initial value problems commonly used in the literature. Finally, we validate the predictions of the modified optimization scheme by performing direct numerical simulations (DNS) that emulate the onset of convection in physical systems.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in porous media Interfacial Flows (free surface): Fingering instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , pp. 456 - 487
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ben, Y., Demekhin, E. A. & Chang, H.-C. 2002 A spectral theory for small-amplitude miscible fingering. Phys. Fluids 14 (3), 999–1010.Google Scholar
Blair, L. M. & Quinn, J. A. 1969 The onset of cellular convection in a fluid layer with time-dependent density gradients. J. Fluid Mech. 36 (02), 385–400.Google Scholar
Caltagirone, J.-P. 1980 Stability of a saturated porous layer subject to a sudden rise in surface temperature: comparison between the linear and energy methods. Q. J. Mech. Appl. Maths 33 (1), 47–58.CrossRefGoogle Scholar
Doumenc, F., Boeck, T., Guerrier, B. & Rossi, M. 2010 Transient Rayleigh–Bénard–Marangoni convection due to evaporation: a linear non-normal stability analysis. J. Fluid Mech. 648, 521–539.Google Scholar
Drazin, P. & Reid, W. 1982 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Elder, J. W. 1968 The unstable thermal interface. J. Fluid Mech. 32 (01), 69–96.Google Scholar
Elenius, M. T., Nordbotten, J. M. & Kalisch, H. 2012 Effects of capillary transition on the stability of a diffusive boundary layer. IMA J. Appl. Maths 77 (6), 771–787.Google Scholar
Ennis-King, J. & Paterson, L. 2005 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. SPE J. 10, 349–356.Google Scholar
Ennis-King, J., Preston, I. & Paterson, L. 2003 Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, Article no. 084107.Google Scholar
Farajzadeh, R., Salimi, H., Zitha, P. L. J. & Bruining, H. 2007 Numerical simulation of density-driven natural convection in porous media with application for ${\mathrm{CO} }_{2} $ injection projects. Intl J. Heat Mass Transfer 50, 5054–5064.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996a Generalized stability theory. Part I. Autonomous operators. J. Atmos. Sci. 53 (14), 2025–2040.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996b Generalized stability theory. Part II. Nonautonomous operators. J. Atmos. Sci. 53 (14), 2041–2053.2.0.CO;2>CrossRefGoogle Scholar
Foster, T. D. 1965 Stability of a homogeneous fluid cooled uniformly from above. Phys. Fluids 8 (7), 1249–1257.Google Scholar
Goldstein, A. W. 1959 Stability of a horizontal fluid layer with unsteady heating from below and time-dependent body force. Tech. Rep. NASA-TR-R-4. NASA.Google Scholar
Green, L. L. & Foster, T. D. 1975 Secondary convection in a Hele Shaw cell. J. Fluid Mech. 71 (04), 675–687.Google Scholar
Gresho, P. M. & Sani, R. L. 1971 The stability of a fluid layer subjected to a step change in temperature: transient vs. frozen time analyses. Intl J. Heat Mass Transfer 14 (2), 207–221.Google Scholar
Jhaveri, B. S. & Homsy, G. M. 1982 The onset of convection in fluid layers heated rapidly in a time-dependent manner. J. Fluid Mech. 114, 251–260.CrossRefGoogle Scholar
Kaviany, M. 1984 Onset of thermal convection in a saturated porous medium: experiment and analysis. Intl J. Heat Mass Transfer 27 (11), 2101–2110.Google Scholar
Kim, M. C. & Choi, C. K. 2011 The stability of miscible displacement in porous media: non-monotonic viscosity profiles. Phys. Fluids 23 (8), 084105.CrossRefGoogle Scholar
Kim, M. C. & Choi, C. K. 2012 Linear stability analysis on the onset of buoyancy-driven convection in liquid-saturated porous medium. Phys. Fluids 24 (4), 044102.Google Scholar
Kim, M. C. & Kim, S. 2005 Onset of convective stability in a fluid-saturated porous layer subjected to time-dependent heating. Intl Commun. Heat Mass Transfer 32, 416–424.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flows. Springer.Google Scholar
Pritchard, D. 2004 The instability of thermal and fluid fronts during radial injection in a porous medium. J. Fluid Mech. 508, 133–163.Google Scholar
Rapaka, S., Chen, S., Pawar, R. J., Stauffer, P. H. & Zhang, D. 2008 Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303.Google Scholar
Rapaka, S., Pawar, R. J., Stauffer, P. H., Zhang, D. & Chen, S. 2009 Onset of convection over a transient base-state in anisotropic and layered porous media. J. Fluid Mech. 641, 227–244.Google Scholar
Rees, D. A. S., Selim, A. & Ennis-King, J. P. 2008 The instability of unsteady boundary layers in porous media. In Emerging Topics in Heat and Mass Transfer in Porous Media (ed. Vadasz, P.), Theory and Applications of Transport in Porous Media, vol. 22, pp. 85–110. Springer.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Selim, A. & Rees, D. A. S. 2007a The stability of a developing thermal front in a porous medium. I. Linear theory. J. Porous Media 10, 1–16.CrossRefGoogle Scholar
Selim, A. & Rees, D. A. S. 2007b The stability of a developing thermal front in a porous medium. II. Nonlinear evolution. J. Porous Media 10 (1), 17–34.Google Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22 (12), 124103.CrossRefGoogle Scholar
Spangenberg, W. G. & Rowland, W. R. 1961 Convective circulation in water induced by evaporative cooling. Phys. Fluids 4, 743–750.Google Scholar
Tan, C. T. & Homsy, G. M. 1986 Stability of miscible displacements in porous media: rectilinear flow. Phys. Fluids 29, 3549–3556.Google Scholar
Wessel-Berg, D. 2009 On a linear stability problem related to underground ${\mathrm{CO} }_{2} $ storage. SIAM J. Appl. Maths 70 (4), 1219–1238.Google Scholar
Whitaker, S. 1999 The Method of Volume Averaging. Kluwer Academic.Google Scholar
Wooding, R. A., Tyler, S. W. & White, I. 1997 Convection in groundwater below an evaporating salt lake: 1. Onset of instability. Water Resour. Res. 33 (6), 1199–1217.Google Scholar