Published online by Cambridge University Press: 30 August 2016
We analyse the influence of the specific features of time-dependent variable-density Kelvin–Helmholtz (VDKH) roll-ups on the development of three-dimensional secondary instabilities. Due to inertial (high Froude number) baroclinic sources of spanwise vorticity at high Atwood number (up to 0.5 here), temporally evolving mixing layers exhibit a layered structure associated with a strain field radically different from their homogeneous counterpart. We use a direct-adjoint non-modal linear approach to determine the fastest growing perturbations over a single period of the time-evolving two-dimensional base flow during a given time interval 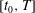 $[t_{0},T]$. When perturbations are seeded at the initial time of the primary KH mode growth, i.e.
$[t_{0},T]$. When perturbations are seeded at the initial time of the primary KH mode growth, i.e. 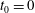 $t_{0}=0$, it is found that additional mechanisms of energy growth are onset around a bifurcation time
$t_{0}=0$, it is found that additional mechanisms of energy growth are onset around a bifurcation time 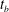 $t_{b}$, a little before the saturation of the primary two-dimensional instability. The evolution of optimal perturbations is thus observed to develop in two distinct stages. Whatever the Atwood number, the first period
$t_{b}$, a little before the saturation of the primary two-dimensional instability. The evolution of optimal perturbations is thus observed to develop in two distinct stages. Whatever the Atwood number, the first period 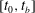 $[t_{0},t_{b}]$ is characterised by a unique route for optimal energy growth resulting from a combination of the Orr and lift-up transient mechanisms. In the second period
$[t_{0},t_{b}]$ is characterised by a unique route for optimal energy growth resulting from a combination of the Orr and lift-up transient mechanisms. In the second period 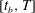 $[t_{b},T]$, the growing influence of mass inhomogeneities raises the energy gain over the whole range of spanwise wavenumbers. As the Atwood number increases, the short spanwise wavelength perturbations tend to benefit more from the onset of variable-density effects than large wavelength ones. The extra energy gain due to increasing Atwood numbers relies on contributions from spanwise baroclinic sources. The resulting vorticity field is structured into two elongated dipoles localised along the braid on either side of the saddle point. In return they yield two longitudinal velocity streaks of opposite sign which account for most of the energy growth. This transition towards three-dimensional motions is in marked contrast with the classic streamwise rib vortices, so far accepted as the paradigm for the transition of free shear flows, either homogeneous or not. It is argued that the emergence of these longitudinal velocity streaks is generic of the transition in variable-density shear flows. Among them, the light round jet is known to display striking side ejections as a result of the loss of axisymmetry. The present analysis helps to renew the question of the underlying flow structure behind side jets, otherwise based on radial induction between pairs of counter-rotating longitudinal vortices (Monkewitz & Pfizenmaier, Phys. Fluids A, vol. 3 (5), 1991, pp. 1356–1361). Instead, it is more likely that side ejections would result from the convergence of the longitudinal velocity streaks near the braid saddle point. When the injection time is delayed so as to suppress the initial stage of energy growth, a new class of perturbations arises at low wavenumber with energy gains far larger than those observed so far. They correspond to the two-dimensional Kelvin–Helmholtz secondary instability of the baroclinically enhanced vorticity braid discovered by Reinaud et al. (Phys. Fluids, vol. 12 (10), pp. 2489–2505), leading potentially to another route to turbulence through a two-dimensional fractal cascade.
$[t_{b},T]$, the growing influence of mass inhomogeneities raises the energy gain over the whole range of spanwise wavenumbers. As the Atwood number increases, the short spanwise wavelength perturbations tend to benefit more from the onset of variable-density effects than large wavelength ones. The extra energy gain due to increasing Atwood numbers relies on contributions from spanwise baroclinic sources. The resulting vorticity field is structured into two elongated dipoles localised along the braid on either side of the saddle point. In return they yield two longitudinal velocity streaks of opposite sign which account for most of the energy growth. This transition towards three-dimensional motions is in marked contrast with the classic streamwise rib vortices, so far accepted as the paradigm for the transition of free shear flows, either homogeneous or not. It is argued that the emergence of these longitudinal velocity streaks is generic of the transition in variable-density shear flows. Among them, the light round jet is known to display striking side ejections as a result of the loss of axisymmetry. The present analysis helps to renew the question of the underlying flow structure behind side jets, otherwise based on radial induction between pairs of counter-rotating longitudinal vortices (Monkewitz & Pfizenmaier, Phys. Fluids A, vol. 3 (5), 1991, pp. 1356–1361). Instead, it is more likely that side ejections would result from the convergence of the longitudinal velocity streaks near the braid saddle point. When the injection time is delayed so as to suppress the initial stage of energy growth, a new class of perturbations arises at low wavenumber with energy gains far larger than those observed so far. They correspond to the two-dimensional Kelvin–Helmholtz secondary instability of the baroclinically enhanced vorticity braid discovered by Reinaud et al. (Phys. Fluids, vol. 12 (10), pp. 2489–2505), leading potentially to another route to turbulence through a two-dimensional fractal cascade.