No CrossRef data available.
Article contents
Optimal perturbation growth in axisymmetric intrusions
Published online by Cambridge University Press: 14 December 2016
Abstract
The cylindrical lock-release laboratory experiments of Sutherland & Nault (J. Fluid Mech., vol. 586, 2007, pp. 109–118) showed that a radially advancing symmetric intrusive gravity current spreads not as an expanding annulus (as is the case for bottom-propagating gravity currents), but rather predominantly along azimuthally periodic radial ‘spokes’. Here, we investigate whether the spokes are associated with azimuthal perturbations that undergo ‘optimal’ growth. We use a nonlinear axisymmetric numerical simulation initialised with the experimental parameters to compute the time-evolving axisymmetric base state of the collapsing lock fluid. Using fields from this rapidly evolving base state together with the linearised perturbation equations and their adjoint, the ‘direct–adjoint looping’ method is employed to identify, as a function of the azimuthal wavenumber 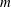 $m$, the vertical–radial structure of the set of initial perturbations that exhibit the largest total perturbation energy gain over a target time
$m$, the vertical–radial structure of the set of initial perturbations that exhibit the largest total perturbation energy gain over a target time 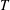 $T$. Of this set of perturbations, the one that extracts energy fastest, and so is expected to be observed to emerge first from the base flow, has azimuthal wavenumber comparable to the number of spokes observed in the experiment.
$T$. Of this set of perturbations, the one that extracts energy fastest, and so is expected to be observed to emerge first from the base flow, has azimuthal wavenumber comparable to the number of spokes observed in the experiment.
- Type
- Rapids
- Information
- Copyright
- © 2016 Cambridge University Press



