Article contents
Optimal mixing in three-dimensional plane Poiseuille flow at high Péclet number
Published online by Cambridge University Press: 10 July 2018
Abstract
We consider a passive zero-mean scalar field organised into two layers of different concentrations in a three-dimensional plane channel flow subjected to a constant along-stream pressure gradient. We employ a nonlinear direct-adjoint-looping method to identify the optimal initial perturbation of the velocity field with given initial energy which yields ‘maximal’ mixing by a target time horizon, where maximal mixing is defined here as the minimisation of the spatially integrated variance of the concentration field. We verify in three-dimensional flows the conjecture by Foures et al. (J. Fluid Mech., vol. 748, 2014, pp. 241–277) that the initial perturbation which maximises the time-averaged energy gain of the flow leads to relatively weak mixing, and is qualitatively different from the optimal initial ‘mixing’ perturbation which exploits classical Taylor dispersion. We carry out the analysis for two different Reynolds numbers (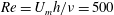 $Re=U_{m}h/\unicode[STIX]{x1D708}=500$ and
$Re=U_{m}h/\unicode[STIX]{x1D708}=500$ and 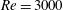 $Re=3000$, where
$Re=3000$, where 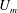 $U_{m}$ is the maximum flow speed of the unperturbed flow,
$U_{m}$ is the maximum flow speed of the unperturbed flow, 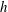 $h$ is the channel half-depth and
$h$ is the channel half-depth and  $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid) demonstrating that this key finding is robust with respect to the transition to turbulence. We also identify the initial perturbations that minimise, at chosen target times, the ‘mix-norm’ of the concentration field, i.e. a Sobolev norm of negative index in the class introduced by Mathew et al. (Physica D, vol. 211, 2005, pp. 23–46). We show that the ‘true’ variance-based mixing strategy can be successfully and practicably approximated by the mix-norm minimisation since we find that the mix-norm-optimal initial perturbations are far less sensitive to changes in the target time horizon than their optimal variance-minimising counterparts.
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid) demonstrating that this key finding is robust with respect to the transition to turbulence. We also identify the initial perturbations that minimise, at chosen target times, the ‘mix-norm’ of the concentration field, i.e. a Sobolev norm of negative index in the class introduced by Mathew et al. (Physica D, vol. 211, 2005, pp. 23–46). We show that the ‘true’ variance-based mixing strategy can be successfully and practicably approximated by the mix-norm minimisation since we find that the mix-norm-optimal initial perturbations are far less sensitive to changes in the target time horizon than their optimal variance-minimising counterparts.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 19
- Cited by



