Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T04:39:11.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Onset of Darcy–Bénard convection in a horizontal layer of dual-permeability medium with isothermal boundaries

Published online by Cambridge University Press:  21 July 2020

Andrey Afanasyev Open the ORCID record for Andrey Afanasyev [Opens in a new window]
Andrey Afanasyev*
Affiliation:
Institute of Mechanics, Moscow State University, Moscow119192, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

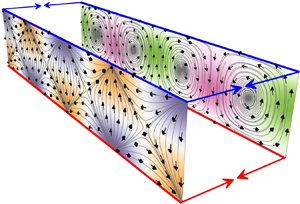
The onset of natural convection in an infinite horizontal layer of a fractured-porous medium is investigated. The breakdown of local equilibrium between the low-permeability matrix and fractures embedded in the matrix is accounted for by applying the dual-porosity dual-permeability model. The symmetric case of impermeable and isothermal boundaries of the layer is examined in detail. By means of linear perturbation analysis, the dispersion equation is derived, and its solutions are investigated numerically as well as analytically in a few asymptotic cases. It is determined that the critical Rayleigh number depends only on the permeability, heat conductivity ratios and the coefficient of heat and mass transfer between fractures and matrix. It is shown that the convection exhibits a rich variety of flow patterns at near-critical conditions. Nine flow regimes can arise with co-rotating or counter-rotating convection cells in the fractures and matrix. These modes can bifurcate to the plane flow regime, in which only cross-medium convection occurs. The complete classification of the flow regimes is provided and plotted in a solution map. Finally, the theoretical analysis is supported by the numerical modelling of the convection by using a reservoir simulator.

JFM classification

Convection: Convection in porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 899 , 25 September 2020 , A18
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afanas'ev, A. A. 2012 A representation of the equations of multicomponent multiphase seepage. J. Appl. Math. Mech. 76 (2), 192–198.CrossRefGoogle Scholar
Afanasyev, A. 2017 Reservoir simulation with the MUFITS code: extension for horizontal wells and fractured reservoirs. Energy Procedia 125, 596–603.CrossRefGoogle Scholar
Afanasyev, A., Blundy, J., Melnik, O. & Sparks, S. 2018 Formation of magmatic brine lenses via focussed fluid-flow beneath volcanoes. Earth Planet. Sci. Lett. 486, 119–128.CrossRefGoogle Scholar
Banu, N. & Rees, D. A. S. 2002 Onset of Darcy–Bénard convection using a thermal non-equilibrium model. Intl J. Heat Mass Transfer 45 (11), 2221–2228.CrossRefGoogle Scholar
Barenblatt, G. I., Zheltov, I. P. & Kochina, I. N. 1960 Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 24 (5), 1286–1303.CrossRefGoogle Scholar
Berre, I., Doster, F. & Keilegavlen, E. 2019 Flow in fractured porous media: a review of conceptual models and discretization approaches. Transp. Porous Med. 130 (1), 215–236.CrossRefGoogle Scholar
Brownell, D. H., Garg, S. K. & Pritchett, J. W. 1977 Governing equations for geothermal reservoirs. Water Resour. Res. 13 (6), 929–934.CrossRefGoogle Scholar
Chen, Z. Q., Cheng, P. & Zhao, T. S. 2000 An experimental study of two phase flow and boiling heat transfer in bi-dispersed porous channels. Intl Commun. Heat Mass Transfer 27 (3), 293–302.CrossRefGoogle Scholar
Davis, S. H. 1969 On the principle of exchange of stabilities. Proc. R. Soc. Lond. A 310 (1502), 341–358.Google Scholar
Diersch, H. J. G. & Kolditz, O. 2002 Variable-density flow and transport in porous media: approaches and challenges. Adv. Water Resour. 25 (8–12), 899–944.CrossRefGoogle Scholar
Dietrich, P., Helmig, R., Sauter, M., Teutsch, G., Hötzl, H. & Köngeter, J. 2005 Flow and Transport in Fractured Porous Media. Springer.CrossRefGoogle Scholar
Ene, H. I. & Sanchez-Palencia, E. 1982 On thermal equation for flow in porous media. Intl J. Engng Sci. 20 (5), 623–630.CrossRefGoogle Scholar
Epherre, J. F. 1975 Apparition criteria of natural-convection in a porous anisotropic layer. Rev. Gén. Therm. 14 (168), 949–950.Google Scholar
Garg, S. K. & Pritchett, J. W. 1977 On pressure-work, viscous dissipation and the energy balance relation for geothermal reservoirs. Adv. Water Resour. 1 (1), 41–47.CrossRefGoogle Scholar
Gérard, A., Genter, A., Kohl, T., Lutz, P., Rose, P. & Rummel, F. 2006 The deep EGS (Enhanced Geothermal System) project at Soultz-sous-Forêts (Alsace, France). Geothermics 35 (5), 473–483.CrossRefGoogle Scholar
Ghanbarian, B. & Daigle, H. 2016 Thermal conductivity in porous media: percolation-based effective-medium approximation. Water Resour. Res. 52 (1), 295–314.CrossRefGoogle Scholar
Horton, C. W. & Rogers, F. T. 1945 Convection currents in a porous medium. J. Appl. Phys. 16 (6), 367–370.CrossRefGoogle Scholar
Kazemi, H., Merrill, L. S., Porterfield, K. L. & Zeman, P. R. 1976 Numerical simulation of water-oil flow in naturally fractured reservoirs. Soc. Petrol. Engng J. 16 (06), 317–326.CrossRefGoogle Scholar
Kvernvold, O. & Tyvand, P. A. 1980 Dispersion effects on thermal-convection in porous-media. J.Fluid Mech. 99, 673–686.CrossRefGoogle Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Proc. Camb. Phil. Soc. 44 (4), 508–521.CrossRefGoogle Scholar
Lim, K. T. & Aziz, K. 1995 Matrix-fracture transfer shape factors for dual-porosity simulators. J. Petrol. Sci. Engng 13, 169–178.CrossRefGoogle Scholar
Magyari, E., Rees, D. A. S. & Keller, B. 2005 Effect of viscous dissipation on the flow in fluid saturated porous media. In Handbook Porous Media, 2nd edn (ed. Vafai, K.), pp. 373–406. Taylor and Francis.Google Scholar
McKibbin, R. & O'Sullivan, M. J. 1980 Onset of convection in a layered porous medium heated from below. J. Fluid Mech. 96 (2), 375–393.CrossRefGoogle Scholar
McKibbin, R. & Tyvand, P. A. 1984 Thermal convection in a porous medium with horizontal cracks. Intl J. Heat Mass Transfer 27 (7), 1007–1023.CrossRefGoogle Scholar
Nie, R. S., Meng, Y. F., Jia, Y. L., Zhang, F. X., Yang, X. T. & Niu, X. N. 2012 Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir. Transp. Porous Med. 92 (1), 213–235.CrossRefGoogle Scholar
Nield, D. A. 1968 Onset of thermohaline convection in a porous medium. Water Resour. Res. 4 (3), 553–560.CrossRefGoogle Scholar
Nield, D. A. & Bejan, A. 2017 Convection in Porous Media, 5th edn. Springer.CrossRefGoogle Scholar
Nield, D. A. & Kuznetsov, A. V. 2006 The onset of convection in a bidisperse porous medium. Intl J. Heat Mass Transfer 49 (17–18), 3068–3074.CrossRefGoogle Scholar
Nield, D. A. & Simmons, C. T. 2007 A discussion on the effect of heterogeneity on the onset of convection in a porous medium. Transp. Porous Med. 68 (3), 413–421.CrossRefGoogle Scholar
Postelnicu, A. & Rees, D. A. S. 2003 The onset of Darcy–Brinkman convection in a porous layer using a thermal nonequlibrium model – part I: stress-free boundaries. Intl J. Energy Res. 27 (10), 961–973.CrossRefGoogle Scholar
Pruess, K. 1983 Heat transfer in fractured geothermal reservoirs with boiling. Water Resour. Res. 19 (1), 201–208.CrossRefGoogle Scholar
Pruess, K. & Narasimhan, T. N. 1985 A practical method for modeling fluid and heat flow in fractured porous media. Soc. Petrol. Engng J. 25 (1), 14–26.CrossRefGoogle Scholar
Rees, D. A. S., Magyari, E. & Keller, B. 2005 Vortex instability of the asymptotic dissipation profile in a porous medium. Transp. Porous Med. 61 (1), 1–14.CrossRefGoogle Scholar
Simmons, C. T. 2005 Variable density groundwater flow: from current challenges to future possibilities. Hydrogeol. J. 13 (1), 116–119.CrossRefGoogle Scholar
Simmons, C. T., Sharp, J. M. & Nield, D. A. 2008 Modes of free convection in fractured low-permeability media. Water Resour. Res. 44 (3), W03431.CrossRefGoogle Scholar
Straughan, B. 2009 On the Nield–Kuznetsov theory for convection in bidispersive porous media. Transp. Porous Med. 77, 159–168.CrossRefGoogle Scholar
Straughan, B. 2015 Convection with Local Thermal Non-equilibrium and Microfluidic Effects. Springer.CrossRefGoogle Scholar
Straughan, B. 2018 Horizontally isotropic bidispersive thermal convection. Proc. R. Soc. Lond. A 474 (2213), 20180018.Google Scholar
Straughan, B. 2019 Horizontally isotropic double porosity convection. Proc. R. Soc. Lond. A 475 (2221), 20180672.Google Scholar
Vujević, K. & Graf, T. 2015 Combined inter- and intra-fracture free convection in fracture networks embedded in a low-permeability matrix. Adv. Water Resour. 84, 52–63.CrossRefGoogle Scholar
Vujević, K., Graf, T., Simmons, C. T. & Werner, A. D. 2014 Impact of fracture network geometry on free convective flow patterns. Adv. Water Resour. 71, 65–80.CrossRefGoogle Scholar
Walker, K. & Homsy, G. M. 1977 A note on convective instabilities in Boussinesq fluids and porous media. J. Heat Transfer 99 (2), 338–339.CrossRefGoogle Scholar
Warren, J. E. & Root, P. J. 1963 The behavior of naturally fractured reservoirs. Soc. Petrol. Engng J. 3(3), 245–255.CrossRefGoogle Scholar
Weis, P. 2015 The dynamic interplay between saline fluid flow and rock permeability in magmatic-hydrothermal systems. Geofluids 15, 350–371.CrossRefGoogle Scholar
Yang, J., Latychev, K. & Edwards, R. N. 1998 Numerical computation of hydrothermal fluid circulation in fractured Earth structures. Geophys. J. Intl 135 (2), 627–649.CrossRefGoogle Scholar

Afanasyev supplementary movie 1

See Movie captions pdf for description
Download Afanasyev supplementary movie 1(Video)
Video 7.3 MB

Afanasyev supplementary movie 2

See Movie captions pdf for description
Download Afanasyev supplementary movie 2(Video)
Video 7 MB

Afanasyev supplementary movie 3

See Movie captions pdf for description
Download Afanasyev supplementary movie 3(Video)
Video 7 MB

Afanasyev supplementary movie 4

See Movie captions pdf for description
Download Afanasyev supplementary movie 4(Video)
Video 6.9 MB
Supplementary material: PDF

Afanasyev supplementary material

Supplementary data

Download Afanasyev supplementary material(PDF)
PDF 151.3 KB
Supplementary material: PDF

Afanasyev supplementary movie captions

Descriptions for Movies 1 to 4

Download Afanasyev supplementary movie captions(PDF)
PDF 14.6 KB