Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-19T22:50:19.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Onset of convection induced by centrifugal buoyancy in a rotating cavity

Published online by Cambridge University Press:  04 August 2017

Diogo B. Pitz Open the ORCID record for Diogo B. Pitz [Opens in a new window] ,
Olaf Marxen  and
John W. Chew
Diogo B. Pitz*
Affiliation:
Department of Mechanical Engineering Sciences, University of Surrey, Guildford, GU2 7XH, UK
Olaf Marxen
Affiliation:
Department of Mechanical Engineering Sciences, University of Surrey, Guildford, GU2 7XH, UK
John W. Chew
Affiliation:
Department of Mechanical Engineering Sciences, University of Surrey, Guildford, GU2 7XH, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Flows induced by centrifugal buoyancy occur in rotating systems in which the centrifugal force is large when compared to other body forces and are of interest for geophysicists and also in engineering problems involving rapid rotation and unstable temperature gradients. In this numerical study we analyse the onset of centrifugal buoyancy in a rotating cylindrical cavity bounded by two plane, insulated disks, adopting a geometrical configuration relevant to fundamental studies of buoyancy-induced flows occurring in gas turbine’s internal air systems. 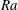Using linear stability analysis, we obtain critical values of the centrifugal Rayleigh number $Ra$ and corresponding critical azimuthal wavenumbers for the onset of convection for different radius ratios. Using direct numerical simulation, we integrate the solutions starting from a motionless state to which small sinusoidal perturbations are added, and show that nonlinear triadic interactions occur before energy saturation takes place. At the lowest Rayleigh number considered, the final state is a limit-cycle oscillation affected by the presence of the disks, having a spectrum dominated by a certain mode and its harmonics. We show that, for this case, the limit-cycle oscillations only develop when no-slip end walls are present. For the largest 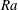$Ra$ considered chaotic motion occurs, but the critical wavenumber obtained from the linear analysis eventually becomes the most energetic even in the turbulent regime.

JFM classification

Convection: Buoyancy-driven instability Geophysical and Geological Flows: Rotating flows Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 484 - 502
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albrecht, T., Blackburn, H. M., Lopez, J. M., Manasseh, R. & Meunier, P. 2015 Triadic resonances in precessing rapidly rotating cylinder flows. J. Fluid Mech. 778, R1.CrossRefGoogle Scholar
Alonso, A., Net, M., Mercader, I. & Knobloch, E. 1999 Onset of convection in a rotating annulus with radial gravity and heating. Fluid Dyn. Res. 24 (3), 133–145.CrossRefGoogle Scholar
Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57 (9), 1435–1458.CrossRefGoogle Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.Google Scholar
Bohn, D., Deuker, E., Emunds, R. & Gorzelitz, V. 1995 Experimental and theoretical investigations of heat transfer in closed gas-filled rotating annuli. Trans. ASME J. Turbomach. 117 (1), 175–183.CrossRefGoogle Scholar
Busse, F. H. & Carrigan, C. R. 1974 Convection induced by centrifugal buoyancy. J. Fluid Mech. 62 (03), 579–592.CrossRefGoogle Scholar
Castrejón-Pita, A. A. & Read, P. L. 2007 Baroclinic waves in an air-filled thermally driven rotating annulus. Phys. Rev. E 75 (2), 026301.Google Scholar
Chew, J. W. & Hills, N. J. 2007 Computational fluid dynamics for turbomachinery internal air systems. Phil. Trans. R. Soc. Lond. A 365 (1859), 2587–2611.Google ScholarPubMed
Früh, W.-G. 2014 Amplitude vacillation in baroclinic flows. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations (ed. von Larcher, T. & Williams, P. D.). Wiley.Google Scholar
Früh, W.-G. & Read, P. L. 1997 Wave interactions and the transition to chaos of baroclinic waves in a thermally driven rotating annulus. Phil. Trans. R. Soc. Lond. A 355 (1722), 101–153.CrossRefGoogle Scholar
Hide, R. 1958 An experimental study of thermal convection in a rotating liquid. Phil. Trans. R. Soc. Lond. A 250 (983), 441–478.Google Scholar
Hide, R. & Mason, P. J. 1975 Sloping convection in a rotating fluid. Adv. Phys. 24 (1), 47–100.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
King, M. P., Wilson, M. & Owen, J. M. 2007 Rayleigh–Bénard convection in open and closed rotating cavities. Trans. ASME: J. Engng Gas Turbines Power 129 (2), 305–311.Google Scholar
Lewis, G. M. & Nagata, W. 2004 Linear stability analysis for the differentially heated rotating annulus. Geophys. Astrophys. Fluid Dyn. 98 (2), 129–152.Google Scholar
Or, A. C. & Busse, F. H. 1987 Convection in a rotating cylindrical annulus. Part 2. Transitions to asymmetric and vacillating flow. J. Fluid Mech. 174, 313–326.CrossRefGoogle Scholar
Owen, J. M. 2010 Thermodynamic analysis of buoyancy-induced flow in rotating cavities. Trans. ASME J. Turbomach. 132 (3), 031006.CrossRefGoogle Scholar
Owen, J. M. & Long, C. A. 2015 Review of buoyancy-induced flow in rotating cavities. Trans. ASME J. Turbomach. 137 (11), 111001.CrossRefGoogle Scholar
Pitz, D. B., Chew, J. W., Marxen, O. & Hills, N. J. 2017 Direct numerical simulation of rotating cavity flows using a spectral element-Fourier method. Trans. ASME: J. Engng Gas Turbines Power 139 (7), 072602.Google Scholar
Randriamampianina, A., Früh, W.-G., Read, P. L. & Maubert, P. 2006 Direct numerical simulations of bifurcations in an air-filled rotating baroclinic annulus. J. Fluid Mech. 561, 359–389.CrossRefGoogle Scholar
Read, P. L., Maubert, P., Randriamampianina, A. & Früh, W.-G. 2008 Direct numerical simulation of transitions towards structural vacillation in an air-filled, rotating, baroclinic annulus. Phys. Fluids 20 (4), 044107.CrossRefGoogle Scholar
Read, P. L., Pérez, E. P., Moroz, I. M. & Young, R. M. B. 2014 General circulation of planetary atmospheres: insights from rotating annulus and related experiments. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations (ed. von Larcher, T. & Williams, P. D.). Wiley.Google Scholar
Rossby, H. T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. In Deep Sea Research and Oceanographic Abstracts, vol. 12, pp. 9IN911–10IN1416. Elsevier.Google Scholar
Schnaubelt, M. & Busse, F. H. 1992 Convection in a rotating cylindrical annulus. Part 3. Vacillating and spatially modulated flows. J. Fluid Mech. 245, 155–173.CrossRefGoogle Scholar
Sheard, G. J., Hussam, W. K. & Tsai, T. 2016 Linear stability and energetics of rotating radial horizontal convection. J. Fluid Mech. 795, 1–35.CrossRefGoogle Scholar
Sun, Z., Kifoil, A., Chew, J. W. & Hills, N. J. 2004 Numerical simulation of natural convection in stationary and rotating cavities. In ASME Turbo Expo 2004: Power for Land, Sea, and Air, pp. 381–389. American Society of Mechanical Engineers.CrossRefGoogle Scholar
Tuckerman, L. S. & Barkley, D. 2000 Bifurcation analysis for timesteppers. In Numerical Methods for Bifurcation Problems and Large-scale Dynamical Systems, pp. 453–466. Springer.Google Scholar
Vincze, M., Borchert, S., Achatz, U., von Larcher, T., Baumann, M., Hertel, C., Remmler, S., Beck, T., Alexandrov, K., Egbers, C. et al. 2015 Benchmarking in a rotating annulus: a comparative experimental and numerical study of baroclinic wave dynamics. Meteorologische Zeitschrift 23, 611–635.CrossRefGoogle Scholar
Zhang, K. & Greed, G. T. 1998 Convection in rotating annulus: an asymptotic theory and numerical solutions. Phys. Fluids 10 (9), 2396–2404.Google Scholar