Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T02:26:45.008Z Has data issue: false hasContentIssue false
  • English
  • Français

On the wake dynamics of a propeller operating in drift

Published online by Cambridge University Press:  31 July 2014

A. Di Mascio ,
R. Muscari  and
G. Dubbioso
A. Di Mascio
Affiliation:
CNR–IAC, Istituto per le Applicazioni del Calcolo ‘Mauro Picone’, Via dei Taurini 19, 00185 Roma RM, Italy
R. Muscari*
Affiliation:
CNR–INSEAN, Istituto Nazionale per Studi ed Esperienze di Architettura Navale, Via di Vallerano 139, 00128 Roma RM, Italy
G. Dubbioso
Affiliation:
CNR–INSEAN, Istituto Nazionale per Studi ed Esperienze di Architettura Navale, Via di Vallerano 139, 00128 Roma RM, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The onset and the nature of dynamic instabilities experienced by the wake of a marine propeller set in oblique flow are investigated by means of detached eddy simulations. In particular, the destabilization process is inspected by a systematic comparison of the wake morphology of a propeller operating in pure axisymmetric flow and in drift with angle of 20°, under different loading conditions. The wake behaviour in oblique flow shows a markedly different character with respect to the axisymmetric condition: in the latter, the destabilization is triggered by an increasing interaction of the main vorticity confined in the tip vortex; whereas, in the former, the role of the secondary vorticity (oriented in the streamwise direction) as well as the hub vortex seems to be crucial. 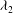The features of the wake have been investigated by the $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\lambda _{2}$ criterion (Jeong & Hussain, J. Fluid Mech., vol. 285, 1995, pp. 69–94) and typical flow variables (pressure, velocity and vorticity), for both the averaged and instantaneous flow fields. Moreover, in order to further inspect the evolution of the vortical structures, as well as their interaction and destabilization, the spectra of the kinetic energy have been considered. This investigation aims to broaden the knowledge from previous works on the subject of rotor wake instabilities, focusing on the differences between an ideal (axisymmetric) and actual operating conditions occurring in typical engineering applications.

JFM classification

Vortex Flows: Vortex instability Vortex Flows: Vortex interactions Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 263 - 307
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beam, R. M. & Warming, R. F. 1978 An implicit factored scheme for the compressible Navier–Stokes equations. AIAA J. 16, 393–402.Google Scholar
Dubbioso, G., Muscari, R. & Di Mascio, A. 2013 Analysis of the performance of a marine propeller in oblique flow. Comput. Fluids 75, 86–102.Google Scholar
Favini, B., Broglia, R. & Di Mascio, A. 1996 Multi-grid acceleration of second order ENO schemes from low subsonic to high supersonic flows. Intl J. Numer. Meth. Fluids 23, 589–606.3.0.CO;2-#>CrossRefGoogle Scholar
Di Felice, F., Di Florio, D., Felli, M. & Romano, G. P. 2004 Experimental investigation of the propeller wake at different loading conditions by particle image velocimetry. J. Ship Res. 48, 168–190.CrossRefGoogle Scholar
Felli, M., Camussi, R. & Di Felice, F. 2011 Mechanism of the evolution of the propeller wake in the transition and far fields. J. Fluid Mech. 682, 5–53.Google Scholar
Felli, M., Di Felice, F., Gui, G. & Camussi, R. 2006 Analysis of the propeller wake evolution by pressure and velocity phase measurements. Exp. Fluids 41, 441–451.Google Scholar
Felli, M., Di Felice, F., Gui, G. & Camussi, R. 2008 Effects of the number of blades on propeller wake evolution. Exp. Fluids 44, 409–418.Google Scholar
Fric, T. F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.CrossRefGoogle Scholar
Grant, I. & Parkin, P. 2000 A DPIV study of the trailing vortex elements from the blades of a horizontal axis wind turbine in yaw. Exp. Fluids 28 (4), 368–376.CrossRefGoogle Scholar
Grant, I., Parkin, P. & Wang, X. 1997 Optical vortex tracking studies of a horizontal axis wind turbine in yaw using laser-sheet, flow visualisation. Exp. Fluids 23 (6), 513–519.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Leishmann, J. G. 2006 Principles of Helicopter Aerodynamics. Wiley.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near field entrainment of a round jet. J. Fluid Mech. 245, 643–668.Google Scholar
Di Mascio, A., Broglia, R. & Favini, B. 2001 A Second Order Godunov-Type Scheme for Naval Hydrodynamics. pp. 253–261. Kluwer Academic/Plenum.Google Scholar
Di Mascio, A., Broglia, R. & Muscari, R. 2007 On the application of the one-phase level set method for naval hydrodynamic flows. Comput. Fluids 36 (5), 868–886.Google Scholar
Di Mascio, A., Broglia, R. & Muscari, R. 2009 Prediction of hydrodynamic coefficients of ship hulls by high-order Godunov-type methods. J. Mar. Sci. Technol. 14, 19–29.Google Scholar
Merkle, C. L. & Athavale, M.1987 Time-accurate unsteady incompressible flow algorithm based on artificially compressibility. AIAA Paper 87-1137.Google Scholar
Muscari, R., Di Mascio, A. & Verzicco, R. 2013 Modeling of vortex dynamics in the wake of a marine propeller. Comput. Fluids 73, 65–79.Google Scholar
Muscari, R., Felli, M. & Di Mascio, A. 2011 Analysis of the flow past a fully appended hull with propellers by computational and experimental fluid dynamics. Trans. ASME: J. Fluids Engng 133 (6), 061104.Google Scholar
Okulov, V. L. 2004 On the stability of multiple helical vortices. J. Fluid Mech. 521, 319–342.CrossRefGoogle Scholar
Okulov, V. L. & Sorensen, J. N. 2007 Stability of helical tip vortices in a rotor far wake. J. Fluid Mech. 576, 1–25.Google Scholar
Okulov, V. L. & Sorensen, J. N. 2010 Applications of 2D helical vortex dynamics. Theor. Comput. Fluid Dyn. 24, 395–401.Google Scholar
Pereira, F., Salvatore, F., Di Felice, F. & Soave, M.2004 Experimental investigation of a cavitating propeller in non-uniform inflow. In Proceedings of 25th Symposium on Naval Hydrodynamics, St. John’s, Newfoundland.Google Scholar
Roache, P. J. 1997 Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 29, 123–160.Google Scholar
Spalart, P. R. & Allmaras, S. R. 1994 A one-equation turbulence model for aerodynamic flows. La Rech. Aérosp. 1, 5–21.Google Scholar
Spalart, P. R., Jou, W.-H., Strelets, M. & Allmaras, S. R. 1997 Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Advances in DNS/LES: Proceedings of the First AFOSR International Conference on DNS/LES, Columbus, OH, pp. 137–147. Greyden Press.Google Scholar
Vermeer, L. J., Sorensen, J. N. & Crespo, A. 2003 Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 39, 467–510.Google Scholar
Yuan, L. L., Street, R. L. & Ferziger, J. H. 1999 LES simulations of a round jet in cross-flow. J. Fluid Mech. 379, 71–104.Google Scholar