Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T11:22:20.024Z Has data issue: false hasContentIssue false
  • English
  • Français

On the spatial segregation of helicity by inertial waves in dynamo simulations and planetary cores

Published online by Cambridge University Press:  19 July 2018

P. A. Davidson Open the ORCID record for P. A. Davidson [Opens in a new window]  and
A. Ranjan Open the ORCID record for A. Ranjan [Opens in a new window]
P. A. Davidson*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
A. Ranjan
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The distribution of kinetic helicity in a dipolar planetary dynamo is central to the success of that dynamo. Motivated by the helicity distributions observed in numerical simulations of the Earth’s dynamo, we consider the relationship between the kinetic helicity, 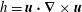$h=\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{u}$, and the buoyancy field that acts as a source of helicity, where $\boldsymbol{u}$ is velocity. We show that, in the absence of a magnetic field, helicity evolves in accordance with the equation 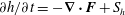$\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}t=-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}+S_{h}$, where the flux, 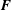$\boldsymbol{F}$, represents the transport of helicity by inertial waves, and the helicity source, $S_{h}$, involves the product of the buoyancy and the velocity fields. In the numerical simulations it is observed that the helicity outside the tangent cylinder is predominantly negative in the north and positive in the south, a feature which the authors had previously attributed to the transport of helicity by waves (Davidson & Ranjan, Geophys. J. Intl, vol. 202, 2015, pp. 1646–1662). It is also observed that there is a strong spatial correlation between the distribution of 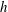$h$ and of 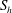$S_{h}$, with 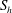$S_{h}$ also predominantly negative in the north and positive in the south. This correlation tentatively suggests that it is the in situ generation of helicity by buoyancy that establishes the distribution of 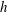$h$ outside the tangent cylinder, rather than the dispersal of helicity by waves, as had been previously argued by the authors. However, although 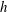$h$ and 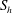$S_{h}$ are strongly correlated, there is no such correlation between 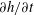$\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}t$ and $S_{h}$, as might be expected if the distribution of 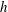$h$ were established by an in situ generation mechanism. We explain these various observations by showing that inertial waves interact with the buoyancy field in such a way as to induce a source 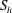$S_{h}$ which has the same sign as the helicity in the local wave flux, and that the sign of 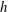$h$ is simply determined by the direction of that flux. We conclude that the observed distributions of 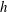$h$ and $S_{h}$ outside the tangent cylinder are consistent with the transport of helicity by waves.

JFM classification

Geophysical and Geological Flows: Geodynamo Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 268 - 287
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardsley, O. P. & Davidson, P. A. 2016 Inertial–Alfvén waves as columnar helices in planetary cores. J. Fluid Mech. 805, R2.Google Scholar
Bardsley, O. P. & Davidson, P. A. 2017 The dispersion of magnetic-Coriolis waves in planetary cores. Geophys. J. Intl 210 (1), 18–26.Google Scholar
Calkins, M. A., Julien, K. & Marti, P. 2013 Three-dimensional quasi-geostrophic convection in the rotating cylindrical annulus with steeply sloping endwalls. J. Fluid Mech. 732, 214–244.Google Scholar
Christensen, U. R. 2010 Dynamo scaling laws and application to the planets. Space Sci. Rev. 152, 565–590.Google Scholar
Christensen, U. R. 2011 Geodynamo models: tools for understanding properties of Earth’s magnetic field. Phys. Earth Planet. Inter. 187, 157–169.Google Scholar
Christensen, U. R. & Wicht, J. 2007 Numerical dynamo simulations. In Treatise on Geophysics (ed. Olson, P.), Elsevier.Google Scholar
Davidson, P. A. 2014 The dynamics and scaling laws of planetary dynamos driven by inertial waves. Geophys. J. Intl 198 (3), 1832–1847.Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Davidson, P. A. & Ranjan, A. 2015 Planetary dynamos driven by helical waves: part 2. Geophys. J. Intl 202, 1646–1662.Google Scholar
Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.Google Scholar
Gilman, P. A. 1977 Nonlinear dynamics of Boussinesq convection in a deep rotating spherical shell. Geophys. Astrophys. Fluid Dyn. 8 (1), 93–135.Google Scholar
Glatzmaier, G. A. & Olson, P. 1993 Highly supercritical thermal convection in a rotating spherical shell: centrifugal versus radial gravity. Geophys. Astrophys. Fluid Dyn. 70 (1–4), 113–136.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hide, R. 1976 A note on helicity. Geophys. Fluid Dyn. 7, 157–161.Google Scholar
Hide, R., Ibbetson, A. & Lighthill, M. J. 1968 On slow transverse flow past obstacles in a rapidly rotating fluid. J. Fluid Mech. 32, 251–272.Google Scholar
Kageyama, A., Watanabe, K. & Sato, T. 1993 Simulation study of a magnetohydrodynamic dynamo: convection in a rotating spherical shell. Phys. Fluids B 5 (8), 2793–2805.Google Scholar
Kitauchi, H., Araki, K. & Kida, S. 1997 Flow structure of thermal convection in a rotating spherical shell. Nonlinearity 10 (4), 885–904.Google Scholar
Kono, M., Sakuraba, A. & Ishida, M. 2000 Dynamo simulation and palaeosecular variation models. Phil. Trans. R. Soc. Lond. A 358, 1123–1139.Google Scholar
Loper, D. E. 2001 On the structure of a Taylor column driven by a buoyant parcel in an unbounded rotating fluid. J. Fluid Mech. 427, 131–165.Google Scholar
Moffatt, H. K. 1970 Dynamo action associated with random inertial waves in a rotating conducting fluid. J. Fluid Mech. 44 (4), 705–719.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Olson, P. 1981 A simple physical model for the terrestrial dynamo. J. Geophys. Res. 86, 10875–10882.Google Scholar
Olson, P., Christensen, U. R. & Glatzmaier, G. A. 1999 Numerical modelling of the geodynamo: mechanisms of field generation and equilibration. J. Geophys. Res. 104 (B5), 10383.Google Scholar
Ranjan, A. 2017 Segregation of helicity in inertial wave packets. Phys. Rev. Fluids 2 (3), 033801.Google Scholar
Ranjan, A. & Davidson, P. A. 2014 Evolution of a turbulent cloud under rotation. J. Fluid Mech. 756, 488–509.Google Scholar
Ranjan, A., Davidson, P. A., Christensen, U. R. & Wicht, J. 2018 Internally driven inertial waves in geodynamo simulations. Geophys. J. Intl 213 (2), 1281–1295.Google Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76 (9), 096801.Google Scholar
Sakuraba, A & Roberts, P. H. 2009 Generation of a strong magnetic field using uniform heat flux at the surface of the core. Nature Geosci. 2, 802–805.Google Scholar
Schaeffer, N., Jault, D., Nataf, H.-C. & Fournier, A. 2017 Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl 211, 1–29.Google Scholar
Shimizu, H. & Loper, D. E. 2000 Small-scale helicity and 𝛼-effect in the Earth’s core. Phys. Earth Planet. Inter. 121, 139–155.Google Scholar
Yadav, R. K., Gastine, T. & Christensen, U. R. 2013 Scaling laws in spherical shell dynamos with free-slip boundaries. Icarus 225, 184–193.Google Scholar
Yeung, P. K. & Zhou, Y. 1998 Numerical study of rotating turbulence with external forcing. Phys. Fluids 10, 2895.Google Scholar