Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T09:22:48.133Z Has data issue: false hasContentIssue false
  • English
  • Français

On the spatial organization of hairpin packets in a turbulent boundary layer at low-to-moderate Reynolds number

Published online by Cambridge University Press:  06 April 2018

Sichao Deng ,
Chong Pan ,
Jinjun Wang Open the ORCID record for Jinjun Wang [Opens in a new window]  and
Guosheng He
Sichao Deng
Affiliation:
Fluid Mechanics Key Laboratory of Ministry of Education, Institute of Fluid Mechanics, Beihang University, Beijing 100191, China
Chong Pan*
Affiliation:
Fluid Mechanics Key Laboratory of Ministry of Education, Institute of Fluid Mechanics, Beihang University, Beijing 100191, China
Jinjun Wang
Affiliation:
Fluid Mechanics Key Laboratory of Ministry of Education, Institute of Fluid Mechanics, Beihang University, Beijing 100191, China
Guosheng He
Affiliation:
Fluid Mechanics Key Laboratory of Ministry of Education, Institute of Fluid Mechanics, Beihang University, Beijing 100191, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

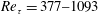The present study is devoted to characterizing the coherent organization of vortical structures, which can be fitted into the paradigm of the hairpin-packet model, in the streamwise–wall-normal plane of a canonical turbulent boundary layer at $Re_{\unicode[STIX]{x1D70F}}=377{-}1093$. Proper orthogonal decomposition (POD) of the planar velocity fields measured via two-dimensional particle image velocimetry, together with a spatio-temporal coherence analysis, shows that the first four leading-order POD modes share both geometric similarity and dynamic coherence and jointly depict the downstream convection of the large-scale Q2/Q4 events, which can be regarded as the low-order imprints of the hairpin packets. A simple low-order indicator is then proposed to extract the inclined interfaces of the hairpin packets, based on which a two-point conditional correlation analysis forms a statistical picture of the spatial organization of multiple prograde vortices aligned along the interface within one packet. A saturation of the self-similar growth of the streamwise gap between two neighbouring vortices is seen. This implies a detachment of the hairpin packets from the inner layer. Both the detachment height and the saturated streamwise spacing are found to scale as 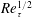$Re_{\unicode[STIX]{x1D70F}}^{1/2}$.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 635 - 668
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.10.1063/1.2717527Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.10.1017/S0022112000001580Google Scholar
Alfredsson, P. H., Segalini, A. & Orlu, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23 (4), 041702.10.1063/1.3581074Google Scholar
Araya, G., Castillo, L. & Hussain, F. 2015 The log behaviour of the Reynolds shear stress in accelerating turbulent boundary layers. J. Fluid Mech. 775, 189–200.10.1017/jfm.2015.296Google Scholar
Asai, M., Minagawa, M. & Nishioka, M. 2002 The instability and breakdown of a near-wall low-speed streak. J. Fluid Mech. 455, 289–314.10.1017/S0022112001007431Google Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.10.1017/jfm.2012.642Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.10.1146/annurev.fl.25.010193.002543Google Scholar
Brandt, L. & de Lange, H. C. 2008 Streak interactions and breakdown in boundary layer flows. Phys. Fluids 20 (2), 024107.10.1063/1.2838594Google Scholar
Brandt, L., Schlatter, P. & Henningson, D. S. 2004 Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 517, 167–198.10.1017/S0022112004000941Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.10.1017/S0022112005004751Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.10.1088/0169-5983/41/2/021404Google Scholar
Chen, J., Hussain, F., Pei, J. & She, Z. S. 2014 Velocity-vorticity correlation structure in turbulent channel flow. J. Fluid Mech. 742, 291–307.10.1017/jfm.2014.3Google Scholar
Chernyshenko, S. I., Di Cicca, G. M., Iollo, A., Smirnov, A. V., Sandham, N. D. & Hu, Z. W. 2006 Analysis of data on the relation between eddies and streaky structures in turbulent flows using the placebo method. Fluid Dyn. 41 (5), 772–783.10.1007/s10697-006-0094-zGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.10.1017/S0022112001003512Google Scholar
Christensen, K. T, Wu, Y., Adrian, R. J. & Lai, W. 2004 Statistical imprints of structure in wall turbulence. In 42nd AIAA Aerospace Sciences Meeting and Exhibit, pp. 7068–7078. AIAA.Google Scholar
Delo, C. J., Kelso, R. M. & Smits, A. J. 2004 Three-dimensional structure of a low-Reynolds-number turbulent boundary layer. J. Fluid Mech. 512, 47–83.10.1017/S0022112004009693Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.10.1017/S0022112010006324Google Scholar
Dennis, D. J. C. & Sogaro, F. M. 2014 Distinct organizational states of fully developed turbulent pipe flow. Phys. Rev. Lett. 113 (23), 234501.10.1103/PhysRevLett.113.234501Google Scholar
Eitel-Amor, G., Orlu, R., Schlatter, P. & Flores, O. 2015 Hairpin vortices in turbulent boundary layers. Phys. Fluids 27 (2), 025108.10.1063/1.4907783Google Scholar
Elsinga, G. E., Adrian, R. J., van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.10.1017/S0022112009992047Google Scholar
Eyink, G. L. 2008 Turbulent flow in pipes and channels as cross-stream ‘inverse cascades’ of vorticity. Phys. Fluids 20 (12), 125101.10.1063/1.3013635Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large-scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.10.1017/S0022112006009244Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.10.1017/S0022112002003270Google Scholar
Gao, Q., Ortiz-Duenas, C. & Longmire, E. K. 2013 Evolution of coherent structures in turbulent boundary layers based on moving tomographic PIV. Exp. Fluids 54 (12), 1625.10.1007/s00348-013-1625-0Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.10.1017/S0022112006008871Google Scholar
He, G. S., Pan, C., Feng, L. H., Gao, Q. & Wang, J. J. 2016 Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer. J. Fluid Mech. 792, 274–306.10.1017/jfm.2016.81Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.10.1017/S0022112081001791Google Scholar
Hellström, L. H., Ganapathisubramani, B. & Smits, A. J. 2015 The evolution of large-scale motions in turbulent pipe flow. J. Fluid Mech. 779, 701–715.10.1017/jfm.2015.418Google Scholar
Hellström, L. H., Marusic, I. & Smits, A. J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.10.1017/jfm.2016.100Google Scholar
Hellström, L. H. & Smits, A. J. 2014 The energetic motions in turbulent pipe flow. Phys. Fluids 26 (12), 125102.10.1063/1.4902436Google Scholar
Hellström, L. H. & Smits, A. J. 2017 Structure identification in pipe flow using proper orthogonal decomposition. Phil. Trans. R. Soc. A 375 (2089), 20160086.Google Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.10.1017/jfm.2012.491Google Scholar
Hong, J., Katz, J., Meneveau, C. & Schultz, M. P. 2012 Coherent structures and associated subgrid-scale energy transfer in a rough-wall turbulent channel flow. J. Fluid Mech. 712, 92–128.10.1017/jfm.2012.403Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Bound.-Layer Meteorol. 145 (2), 273–306.10.1007/s10546-012-9735-4Google Scholar
Hutchins, N., Hambleton, W. T. & Marusic, I. 2005 Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 541, 21–54.10.1017/S0022112005005872Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.10.1017/S0022112096003965Google Scholar
Jimenez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.10.1017/S0022112010001370Google Scholar
Jodai, Y. & Elsinga, G. E. 2016 Experimental observation of hairpin auto-generation events in a turbulent boundary layer. J. Fluid Mech. 795, 611–633.10.1017/jfm.2016.153Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.10.1063/1.869889Google Scholar
Kim, K. Y., Sung, H. J. & Adrian, R. J. 2008 Effects of background noise on generating coherent packets of hairpin vortices. Phys. Fluids 20 (10), 105107.10.1063/1.3001797Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638 (638), 73–93.10.1017/S002211200999084XGoogle Scholar
Liu, Z., Adrian, R. J. & Hanratty, T. J. 2001 Large-scale modes of turbulent channel flow: transport and structure. J. Fluid Mech. 448, 53–80.10.1017/S0022112001005808Google Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60 (3), 481–511.10.1017/S0022112073000315Google Scholar
Lumley, J. L. 1981 Coherent structures in turbulence. In Transition and Turbulence (ed. Meyer, R. E.), pp. 215–242. Academic.10.1016/B978-0-12-493240-1.50017-XGoogle Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.10.1063/1.1343480Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.10.1063/1.1589014Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.10.1017/jfm.2012.511Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.10.1017/S0022112095003363Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.10.1017/S0022112009006946Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.10.1063/1.868594Google Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.10.1017/jfm.2013.61Google Scholar
Meneveau, C. & Marusic, I. 2017 Turbulence in the Era of Big Data: Recent Experiences with Sharing Large Datasets, pp. 497–507. Springer.Google Scholar
Moin, P. & Moser, R. D. 1989 Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 200, 471–509.10.1017/S0022112089000741Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.10.1017/S0022112004008985Google Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365 (1852), 755–770.10.1098/rsta.2006.1948Google Scholar
Natrajan, V. K. & Christensen, K. T. 2006 The role of coherent structures in subgrid-scale energy transfer within the log layer of wall turbulence. Phys. Fluids 18 (6), 065104.10.1063/1.2206811Google Scholar
Natrajan, V. K., Wu, Y. & Christensen, K. T. 2007 Spatial signatures of retrograde spanwise vortices in wall turbulence. J. Fluid Mech. 574, 155–167.10.1017/S0022112006003788Google Scholar
Pan, C., Wang, J. J. & He, G. S. 2012 Experimental investigation of wake-induced bypass transition control by surface roughness. Chin. Phys. Lett. 29 (10), 104704.10.1088/0256-307X/29/10/104704Google Scholar
Pan, C., Wang, J. J. & Zhang, C. 2009 Identification of Lagrangian coherent structures in the turbulent boundary layer. Sci. China Ser. G 52 (2), 248–257.10.1007/s11433-009-0033-1Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.10.1017/S0022112082001311Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.10.1017/S0022112095003351Google Scholar
Rempfer, D. & Fasel, H. F. 1994 Evolution of three-dimensional coherent structures in a flat-plate boundary layer. J. Fluid Mech. 260, 351–375.10.1017/S0022112094003551Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.10.1146/annurev.fl.23.010191.003125Google Scholar
Sayadi, T., Hamman, C. W. & Moin, P. 2013 Direct numerical simulation of complete H-type and K-type transitions with implications for the dynamics of turbulent boundary layers. J. Fluid Mech. 724, 480509.10.1017/jfm.2013.142Google Scholar
Scarano, F. & Riethmuller, M. L. 2000 Advances in iterative multigrid PIV image processing. Exp. Fluids 29 (S), S51–S60.10.1007/s003480070007Google Scholar
Schlatter, P., Li, Q., Orlu, R., Hussain, F. & Henningson, D. S. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. Mech. B 48, 75–93.10.1016/j.euromechflu.2014.04.011Google Scholar
Schlatter, P. & Orlu, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.10.1017/S0022112010003113Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.10.1017/S002211200100667XGoogle Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.10.1017/jfm.2015.672Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures: I, II, III. Q. Appl. Maths 45 (3), 561–571.10.1090/qam/910462Google Scholar
Smith, C. R., Walker, J. D. A., Haidari, A. H. & Sobrun, U. 1991 On the dynamics of near-wall turbulence. Phil. Trans. R. Soc. Lond. 336, 131–175.Google Scholar
Sreenivasan, K. R. 1989 The turbulent boundary layer. Front. Exp. Fluid Mech. 159–209.10.1007/978-3-642-83831-6_4Google Scholar
Tian, H. P., Zhang, J. X., Jiang, N. & Yao, Z. H. 2015 Effect of hierarchical structured superhydrophobic surfaces on coherent structures in turbulent channel flow. Exp. Therm. Fluid Sci. 69, 27–37.10.1016/j.expthermflusci.2015.07.018Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.10.1017/S0022112003005251Google Scholar
Townsend, A. A. 1976 The Structure Of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vila, C. S., Vinuesa, R., Discetti, S., Ianiro, A., Schlatter, P. & Örlü, R. 2017 On the identification of well-behaved turbulent boundary layers. J. Fluid Mech. 822, 109–138.10.1017/jfm.2017.258Google Scholar
Wang, G. H. & Zheng, X. J. 2016 Very large scale motions in the atmospheric surface layer: a field investigation. J. Fluid Mech. 802, 464–489.10.1017/jfm.2016.439Google Scholar
Wang, J. J., Pan, C. & Zhang, P. F. 2009 On the instability and reproduction mechanism of a laminar streak. J. Turbul. 10, N26.10.1080/14685240902906127Google Scholar
Wu, X. 2017 Inflow turbulence generation methods. Annu. Rev. Fluid Mech. 49, 23–49.10.1146/annurev-fluid-010816-060322Google Scholar
Wu, X. H. & Moin, P. 2009a Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.10.1017/S0022112009006624Google Scholar
Wu, X. H. & Moin, P. 2009b Forest of hairpins in a low-Reynolds-number zero-pressure-gradient flat-plate boundary layer. Phys. Fluids 21 (9), 091106.10.1063/1.3205471Google Scholar
Wu, X. H., Moin, P. & Hickey, J. P. 2014 Boundary layer bypass transition. Phys. Fluids 26 (9), 091104.10.1063/1.4893454Google Scholar
Wu, Y. 2014 A study of energetic large-scale structures in turbulent boundary layer. Phys. Fluids 26 (4), 045113.10.1063/1.4873199Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.10.1017/S002211200600259XGoogle Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.10.1017/S0022112010000960Google Scholar
Zhao, Y. M., Yang, Y. & Chen, S. Y. 2016 Vortex reconnection in the late transition in channel flow. J. Fluid Mech. 802, R4.10.1017/jfm.2016.492Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.10.1017/S002211209900467XGoogle Scholar

Deng et al. supplementary movie

An animation corresponding to Figure 12(a) to depict the time evolution of the large-scale interface revealed in $\bm{V}^L$ at the case of $Re_{ au}=377$.

Download Deng et al. supplementary movie(Video)
Video 8.3 MB