Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T06:36:28.159Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface

Published online by Cambridge University Press:  19 August 2014

V. K. Tritschler ,
B. J. Olson ,
S. K. Lele ,
S. Hickel Open the ORCID record for S. Hickel [Opens in a new window] ,
X. Y. Hu  and
N. A. Adams
V. K. Tritschler*
Affiliation:
Institute of Aerodynamics and Fluid Mechanics, Technische Universität München, 85747 Garching, Germany Department of Aeronautics and Astronautics, Stanford University, Stanford, CA 94305, USA
B. J. Olson
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
S. K. Lele
Affiliation:
Department of Aeronautics and Astronautics, Stanford University, Stanford, CA 94305, USA
S. Hickel
Affiliation:
Institute of Aerodynamics and Fluid Mechanics, Technische Universität München, 85747 Garching, Germany
X. Y. Hu
Affiliation:
Institute of Aerodynamics and Fluid Mechanics, Technische Universität München, 85747 Garching, Germany
N. A. Adams
Affiliation:
Institute of Aerodynamics and Fluid Mechanics, Technische Universität München, 85747 Garching, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the shock-induced turbulent mixing between a light and a heavy gas, where a Richtmyer–Meshkov instability (RMI) is initiated by a shock wave with Mach number 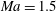$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ma}= 1.5$. The prescribed initial conditions define a deterministic multimode interface perturbation between the gases, which can be imposed exactly for different simulation codes and resolutions to allow for quantitative comparison. Well-resolved large-eddy simulations are performed using two different and independently developed numerical methods with the objective of assessing turbulence structures, prediction uncertainties and convergence behaviour. The two numerical methods differ fundamentally with respect to the employed subgrid-scale regularisation, each representing state-of-the-art approaches to RMI. Unlike previous studies, the focus of the present investigation is to quantify the uncertainties introduced by the numerical method, as there is strong evidence that subgrid-scale regularisation and truncation errors may have a significant effect on the linear and nonlinear stages of the RMI evolution. Fourier diagnostics reveal that the larger energy-containing scales converge rapidly with increasing mesh resolution and thus are in excellent agreement for the two numerical methods. Spectra of gradient-dependent quantities, such as enstrophy and scalar dissipation rate, show stronger dependences on the small-scale flow field structures as a consequence of truncation error effects, which for one numerical method are dominantly dissipative and for the other dominantly dispersive. Additionally, the study reveals details of various stages of RMI, as the flow transitions from large-scale nonlinear entrainment to fully developed turbulent mixing. The growth rates of the mixing zone widths as obtained by the two numerical methods are 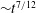${\sim } t^{7/12}$ before re-shock and 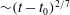${\sim } (t-t_0)^{2/7}$ long after re-shock. The decay rate of turbulence kinetic energy is consistently 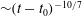${\sim } (t-t_0)^{-10/7}$ at late times, where the molecular mixing fraction approaches an asymptotic limit $\varTheta \approx 0.85$. The anisotropy measure 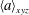$\langle a \rangle _{xyz}$ approaches an asymptotic limit of 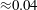${\approx }0.04$, implying that no full recovery of isotropy within the mixing zone is obtained, even after re-shock. Spectra of density, turbulence kinetic energy, scalar dissipation rate and enstrophy are presented and show excellent agreement for the resolved scales. The probability density function of the heavy-gas mass fraction and vorticity reveal that the light–heavy gas composition within the mixing zone is accurately predicted, whereas it is more difficult to capture the long-term behaviour of the vorticity.

JFM classification

Compressible Flows: Shock waves Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 429 - 462
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aglitskiy, Y., Velikovich, A. L., Karasik, M., Metzler, N., Zalesak, S. T., Schmitt, A. J., Phillips, L., Gardner, J. H., Serlin, V., Weaver, J. L. & Obenschain, S. P. 2010 Basic hydrodynamics of Richtmyer–Meshkov-type growth and oscillations in the inertial confinement fusion-relevant conditions. Phil. Trans. R. Soc. Lond. A 368 (1916), 1739–1768.Google Scholar
Almgren, A. S., Bell, J. B., Rendleman, C. A. & Zingale, M. 2006 Low Mach number modeling of type Ia supernovae I. Hydrodynamics. Astrophys. J. 637, 922–936.Google Scholar
Arnett, D. 2000 The role of mixing in astrophysics. Astrophys. J. Suppl. 127, 213–217.CrossRefGoogle Scholar
Arnett, W. D., Bahcall, J. N., Kirshner, R. P. & Stanford, E. W. 1989 Supernova 1987a. Annu. Rev. Astron. Astrophys. 27, 629–700.CrossRefGoogle Scholar
Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.CrossRefGoogle Scholar
Balasubramanian, S., Orlicz, G. C. & Prestridge, K. P. 2013 Experimental study of initial condition dependence on turbulent mixing in shock-accelerated Richtmyer–Meshkov fluid layers. J. Turbul. 14 (3), 170–196.Google Scholar
Balasubramanian, S., Orlicz, G. C., Prestridge, K. P. & Balakumar, B. J. 2012 Experimental study of initial condition dependence on Richtmyer–Meshkov instability in the presence of reshock. Phys. Fluids 24, 034103.Google Scholar
Batchelor, G. K. & Proudman, I. 1956 The large-scale structure of homogeneous turbulence. Phil. Trans. R. Soc. Lond. A 248, 369–405.Google Scholar
Besnard, D., Harlow, F. H., Rauenzahn, R. M. & Zemach, C.1992 Turbulence transport equations for variable-density turbulence and their relationship to two-field models. Recon Tech. Rep. No. 92, 33159. NASA STI.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Cabot, W. H. & Cook, A. W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type Ia supernovae. Nat. Phys. 2 (8), 562–568.CrossRefGoogle Scholar
Chapman, S. & Cowling, T. G. 1990 The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity. Cambridge University Press.Google Scholar
Cohen, R. H., Dannevik, W. P., Dimits, A. M., Eliason, D. E., Mirin, A. A., Zhou, Y., Porter, D. H. & Woodward, P. R. 2002 Three-dimensional simulation of a Richtmyer–Meshkov instability with a two-scale initial perturbation. Phys. Fluids 14 (10), 3692–3709.Google Scholar
Cook, A. W. 2007 Artificial fluid properties for large-eddy simulation of compressible turbulent mixing. Phys. Fluids 19 (5), 055103.Google Scholar
Cook, A. W. 2009 Enthalpy diffusion in multicomponent flows. Phys. Fluids 21, 055109.Google Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.Google Scholar
Dimonte, G., Frerking, C. E. & Schneider, M. 1995 Richtmyer–Meshkov instability in the turbulent regime. Phys. Rev. Lett. 74, 4855–4858.CrossRefGoogle ScholarPubMed
Dimonte, G. & Schneider, M. 2000 Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12 (2), 304–321.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Drikakis, D. 2003 Advances in turbulent flow computations using high-resolution methods. Prog. Aerosp. Sci. 39 (6–7), 405–424.Google Scholar
Drikakis, D., Hahn, M., Mosedale, A. & Thornber, B. 2009 Large eddy simulation using high-resolution and high-order methods. Phil. Trans. R. Soc. Lond. A 367 (1899), 2985–2997.Google Scholar
Fedkiw, R. P., Merriman, B. & Osher, S. 1997 High accuracy numerical methods for thermally perfect gas flows with chemistry. J. Comput. Phys. 190, 175–190.CrossRefGoogle Scholar
Gottlieb, S. & Shu, C.-W. 1998 Total variation diminishing Runge–Kutta schemes. Math. Comput. 67, 73.CrossRefGoogle Scholar
Grinstein, F. F., Gowardhan, A. A. & Wachtor, A. J. 2011 Simulations of Richtmyer–Meshkov instabilities in planar shock-tube experiments. Phys. Fluids 23, 034106.Google Scholar
Hahn, M., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Richtmyer–Meshkov turbulent mixing arising from an inclined material interface with realistic surface perturbations and reshocked flow. Phys. Fluids 23 (4), 046101.Google Scholar
Hill, D. J., Pantano, C. & Pullin, D. I. 2006 Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.CrossRefGoogle Scholar
Hill, D. J. & Pullin, D. I. 2004 Hybrid tuned center-difference-WENO method for large eddy simulations in the presence of strong shocks. J. Comput. Phys. 194, 435–450.Google Scholar
Hu, X. Y. & Adams, N. A. 2011 Scale separation for implicit large eddy simulation. J. Comput. Phys. 230 (19), 7240–7249.Google Scholar
Hu, X. Y., Adams, N. A. & Shu, C.-W. 2013 Positivity-preserving method for high-order conservative schemes solving compressible Euler equations. J. Comput. Phys. 242, 169–180.Google Scholar
Hu, X. Y., Wang, Q. & Adams, N. A. 2010 An adaptive central-upwind weighted essentially non-oscillatory scheme. J. Comput. Phys. 229 (23), 8952–8965.Google Scholar
Ishida, T., Davidson, P. A. & Kaneda, Y. 2006 On the decay of isotropic turbulence. J. Fluid Mech. 564, 455–475.Google Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Kennedy, C. A., Carpenter, M. H. & Lewis, M. R. 2000 Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Maths 35 (3), 177–219.CrossRefGoogle Scholar
Khokhlov, A. M., Oran, E. S. & Thomas, G. O. 1999 Numerical simulation of deflagration-to-detonation transition: the role of shock–flame interactions in turbulent flames. Combust. Flame 117 (1–2), 323–339.Google Scholar
Kolmogorov, A. N. 1941 On the degeneration of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 31, 538–541.Google Scholar
Kosović, B., Pullin, D. I. & Samtaney, R. 2002 Subgrid-scale modeling for large-eddy simulations of compressible turbulence. Phys. Fluids 14 (4), 1511–1522.Google Scholar
Larouturou, B. & Fezoui, L. 1989 On the equations of multi-component perfect or real gas inviscid flow. In Nonlinear Hyperbolic Problems, Lecture Notes in Mathematics, vol. 1402, pp. 69–97. Springer.Google Scholar
Lele, S. K. 1992 Compact finite-difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Lindl, J. D., McCrory, R. L. & Campbell, E. M. 1992 Progress toward ignition and burn propagation in inertial confinement fusion. Phys. Today 45 (9), 32–40.Google Scholar
Llor, A.2006 Invariants of free turbulent decay, arXiv:physics/0612220.Google Scholar
Lombardini, M., Hill, D. J., Pullin, D. I. & Meiron, D. I. 2011 Atwood ratio dependence of Richtmyer–Meshkov flows under reshock conditions using large-eddy simulations. J. Fluid Mech. 670, 439–480.Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2012 Transition to turbulence in shock-driven mixing: a Mach number study. J. Fluid Mech. 690, 203–226.Google Scholar
Mani, A., Larsson, J. & Moin, P. 2009 Suitability of artificial bulk viscosity for large-eddy simulation of turbulent flows with shocks. J. Comput. Phys. 228 (19), 7368–7374.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 151–157.Google Scholar
Mikaelian, K. O. 1989 Turbulent mixing generated by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Physica D 36 (3), 343–357.Google Scholar
Olson, B. J. & Cook, A. W. 2007 Rayleigh–Taylor shock waves. Phys. Fluids 19, 128108.Google Scholar
Olson, B. J., Larsson, J., Lele, S. K. & Cook, A. W. 2011 Non-linear effects in the combined Rayleigh–Taylor/Kelvin–Helmholtz instability. Phys. Fluids 23, 114107.Google Scholar
Orlicz, G. C., Balasubramanian, S. & Prestridge, K. P. 2013 Incident shock Mach number effects on Richtmyer–Meshkov mixing in a heavy gas layer. Phys. Fluids 25 (11), 114101.Google Scholar
Pullin, D. I. 2000 A vortex-based model for the subgrid flux of a passive scalar. Phys. Fluids 12 (9), 2311–2319.Google Scholar
Ramshaw, J. D. 1990 Self-consistent effective binary diffusion in multicomponent gas mixtures. J. Non-Equilib. Thermodyn. 15, 295–300.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Reid, R. C., Pransuitz, J. M. & Poling, B. E. 1987 The Properties of Gases and Liquids. McGraw-Hill.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.CrossRefGoogle Scholar
Roe, P. L. 1981 Approximate Riemann solvers, parameter and difference schemes. J. Comput. Phys. 43, 357–372.Google Scholar
Saffman, P. G. 1967a Note on decay of homogeneous turbulence. Phys. Fluids 10, 1349.CrossRefGoogle Scholar
Saffman, P. G. 1967b The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.Google Scholar
Schilling, O. & Latini, M. 2010 High-order WENO simulations of three-dimensional reshocked Richtmyer–Meshkov instability to late times: dynamics, dependence on initial conditions, and comparisons to experimental data. Acta Math. Sci. 30B, 595–620.Google Scholar
Schilling, O., Latini, M. & Don, W. S. 2007 Physics of reshock and mixing in single-mode Richtmyer–Meshkov instability. Phys. Rev. E 76, 026319.CrossRefGoogle ScholarPubMed
Taccetti, J. M., Batha, S. H., Fincke, J. R., Delamater, N. D., Lanier, N. E., Magelssen, G. R., Hueckstaedt, R. M., Rothman, S. D., Horsfield, C. J. & Parker, K. W. 2005 Richtmyer–Meshkov instability reshock experiments using laser-driven double-cylinder implosions. In High Energy Density Laboratory Astrophysics (ed. Kyrala, G. A.), pp. 327–331. Springer.CrossRefGoogle Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Part 1. Waves on fluid sheets. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2010 The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability. J. Fluid Mech. 654, 99–139.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Growth of a Richtmyer–Meshkov turbulent layer after reshock. Phys. Fluids 23, 095107.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2012 Physics of the single-shocked and reshocked Richtmyer–Meshkov instability. J. Turbul. 13 (1), N10.Google Scholar
Thornber, B., Mosedale, A., Drikakis, D., Youngs, D. & Williams, R. J. R. 2008 An improved reconstruction method for compressible flows with low Mach number features. J. Comput. Phys. 227 (10), 4873–4894.Google Scholar
Tomkins, C. D., Balakumar, B. J., Orlicz, G., Prestridge, K. P. & Ristorcelli, J. R. 2013 Evolution of the density self-correlation in developing Richtmyer–Meshkov turbulence. J. Fluid Mech. 735, 288–306.Google Scholar
Toro, E. F. 1999 Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer.Google Scholar
Tritschler, V. K., Avdonin, A., Hickel, S., Hu, X. Y. & Adams, N. A. 2014 Quantification of initial-data uncertainty on a shock-accelerated gas cylinder. Phys. Fluids 26 (2), 026101.CrossRefGoogle Scholar
Tritschler, V. K., Hickel, S., Hu, X. Y. & Adams, N. A. 2013a On the Kolmogorov inertial subrange developing from Richtmyer–Meshkov instability. Phys. Fluids 25, 071701.Google Scholar
Tritschler, V. K., Hu, X. Y., Hickel, S. & Adams, N. A. 2013b Numerical simulation of a Richtmyer–Meshkov instability with an adaptive central-upwind 6th-order WENO scheme. Phys. Scr. T155, 014016.CrossRefGoogle Scholar
Weber, C. R., Cook, A. W. & Bonazza, R. 2013 Growth rate of a shocked mixing layer with known initial perturbations. J. Fluid Mech. 725, 372–401.Google Scholar
Weber, C., Haehn, N., Oakley, J., Rothamer, D. & Bonazza, R. 2012 Turbulent mixing measurements in the Richtmyer–Meshkov instability. Phys. Fluids 24, 074105.Google Scholar
Weber, C. R., Haehn, N. S., Oakley, J. G., Rothamer, D. A. & Bonazza, R. 2014 An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability. J. Fluid Mech. 748, 457–487.Google Scholar
Wilczek, M., Daitche, A. & Friedrich, R. 2011 On the velocity distribution in homogeneous isotropic turbulence: correlations and deviations from gaussianity. J. Fluid Mech. 676, 191–217.Google Scholar
Yang, J., Kubota, T. & Zukoski, E. E. 1993 Applications of shock-induced mixing to supersonic combustion. AIAA J. 31, 854–862.Google Scholar
Youngs, D. L. 1991 Three-dimensional numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Phys. Fluids A: Fluid Dyn. 3 (5), 1312–1320.Google Scholar
Youngs, D. L. 1994 Numerical simulations of mixing by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Laser Part. Beams 12 (2), 538–544.Google Scholar
Youngs, D. L.2004 Effect of initial conditions on self-similar turbulent mixing. In Proceedings of the International Workshop on the Physics of Compressible Turbulent Mixing, vol. 9.Google Scholar
Youngs, D. L. 2007 Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics, pp. 392–412. Cambridge University Press.Google Scholar
Zabusky, N. J. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31, 495–536.Google Scholar
Zhou, Y. 2001 A scaling analysis of turbulent flows driven by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Fluids 13 (2), 538–543.Google Scholar