Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lozano-Durán, Adrián
Nikolaidis, Marios-Andreas
Constantinou, Navid C.
and
Karp, Michael
2020.
Alternative physics to understand wall turbulence: Navier–Stokes equations with modified linear dynamics.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012003.
Bae, H. Jane
Dawson, Scott T. M.
and
McKeon, Beverley J.
2020.
Resolvent-based study of compressibility effects on supersonic turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Zare, A.
Georgiou, T.T.
and
Jovanović, M.R.
2020.
Stochastic Dynamical Modeling of Turbulent Flows.
Annual Review of Control, Robotics, and Autonomous Systems,
Vol. 3,
Issue. 1,
p.
195.
Hwang, Yongyun
and
Eckhardt, Bruno
2020.
Attached eddy model revisited using a minimal quasi-linear approximation.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Karban, U.
Bugeat, B.
Martini, E.
Towne, A.
Cavalieri, A. V. G.
Lesshafft, L.
Agarwal, A.
Jordan, P.
and
Colonius, T.
2020.
Ambiguity in mean-flow-based linear analysis.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Symon, S.
Illingworth, S. J.
and
Marusic, I.
2020.
Large-scale structures predicted by linear models of wall-bounded turbulence.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012006.
Abreu, Leandra I.
Cavalieri, André V.G.
Schlatter, Philipp
Vinuesa, Ricardo
and
Henningson, Dan S.
2020.
Resolvent modelling of near-wall coherent structures in turbulent channel flow.
International Journal of Heat and Fluid Flow,
Vol. 85,
Issue. ,
p.
108662.
Pickering, Ethan
Rigas, Georgios
Nogueira, Petrônio A. S.
Cavalieri, André V. G.
Schmidt, Oliver T.
and
Colonius, Tim
2020.
Lift-up, Kelvin–Helmholtz and Orr mechanisms in turbulent jets.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Yang, Bowen
Jin, Guodong
Wu, Ting
Yang, Zixuan
and
He, Guowei
2020.
Numerical implementation and evaluation of resolvent-based estimation for space–time energy spectra in turbulent channel flows.
Acta Mechanica Sinica,
Vol. 36,
Issue. 4,
p.
775.
Liu, Chang
and
Gayme, Dennice F.
2020.
An input–output based analysis of convective velocity in turbulent channels.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Towne, Aaron
Lozano-Durán, Adrián
and
Yang, Xiang
2020.
Resolvent-based estimation of space–time flow statistics.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Wu, Ting
and
He, Guowei
2021.
Stochastic dynamical model for space-time energy spectra in turbulent shear flows.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Bae, H. Jane
Lozano-Durán, A.
and
McKeon, Beverley J.
2021.
Nonlinear mechanism of the self-sustaining process in the buffer and logarithmic layer of wall-bounded flows.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Pickering, Ethan
Rigas, Georgios
Schmidt, Oliver T.
Sipp, Denis
and
Colonius, Tim
2021.
Optimal eddy viscosity for resolvent-based models of coherent structures in turbulent jets.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Chavarin, A.
Gómez-de-Segura, G.
García-Mayoral, R.
and
Luhar, M.
2021.
Resolvent-based predictions for turbulent flow over anisotropic permeable substrates.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Negi, P.S.
Hanifi, A.
and
Henningson, D.S.
2021.
On the onset of aeroelastic pitch-oscillations of a NACA0012 wing at transitional Reynolds numbers.
Journal of Fluids and Structures,
Vol. 105,
Issue. ,
p.
103344.
Jovanović, Mihailo R.
2021.
From Bypass Transition to Flow Control and Data-Driven Turbulence Modeling: An Input–Output Viewpoint.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
311.
Pickering, Ethan
Towne, Aaron
Jordan, Peter
and
Colonius, Tim
2021.
Resolvent-based modeling of turbulent jet noise.
The Journal of the Acoustical Society of America,
Vol. 150,
Issue. 4,
p.
2421.
Nogueira, Petrônio A. S.
Morra, Pierluigi
Martini, Eduardo
Cavalieri, André V. G.
and
Henningson, Dan S.
2021.
Forcing statistics in resolvent analysis: application in minimal turbulent Couette flow.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Morra, Pierluigi
Nogueira, Petrônio A. S.
Cavalieri, André V. G.
and
Henningson, Dan S.
2021.
The colour of forcing statistics in resolvent analyses of turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 907,
Issue. ,
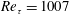 $\text{Re}_{\unicode[STIX]{x1D70F}}=1007$. The analysis is performed for spatial scales characteristic of buffer-layer and large-scale motions by separating the contributions of different temporal frequencies. Good agreement between the measured spatio-temporal power spectral densities and those estimated by means of the resolvent is found when the effect of turbulent Reynolds stresses, modelled with an eddy-viscosity associated with the turbulent mean flow, is included in the resolvent operator. The agreement is further improved when the flat forcing power spectrum (white noise) is replaced with a power spectrum matching the measures. Such a good agreement is not observed when the eddy-viscosity terms are not included in the resolvent operator. In this case, the estimation based on the resolvent is unable to select the right peak frequency and wall-normal location of buffer-layer motions. Similar results are found when comparing truncated expansions of measured streamwise velocity power spectral densities based on a spectral proper orthogonal decomposition to those obtained with optimal resolvent modes.
$\text{Re}_{\unicode[STIX]{x1D70F}}=1007$. The analysis is performed for spatial scales characteristic of buffer-layer and large-scale motions by separating the contributions of different temporal frequencies. Good agreement between the measured spatio-temporal power spectral densities and those estimated by means of the resolvent is found when the effect of turbulent Reynolds stresses, modelled with an eddy-viscosity associated with the turbulent mean flow, is included in the resolvent operator. The agreement is further improved when the flat forcing power spectrum (white noise) is replaced with a power spectrum matching the measures. Such a good agreement is not observed when the eddy-viscosity terms are not included in the resolvent operator. In this case, the estimation based on the resolvent is unable to select the right peak frequency and wall-normal location of buffer-layer motions. Similar results are found when comparing truncated expansions of measured streamwise velocity power spectral densities based on a spectral proper orthogonal decomposition to those obtained with optimal resolvent modes.

