Published online by Cambridge University Press: 19 February 2019
The Green–Naghdi equations are an extension of the shallow-water equations that capture the effects of finite fluid depth at arbitrary order in the characteristic height to width aspect ratio 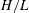 $H/L$. The shallow-water equations capture these effects to first order only, resulting in a relatively simple two-dimensional fluid-dynamical model for the layer horizontal velocity and depth. The Green–Naghdi equations, like the shallow-water equations, are two-dimensional fluid equations expressing momentum and mass conservation. There are different ‘levels’ of the Green–Naghdi equations of rapidly increasing complexity. In the present paper we focus on the behaviour of the lowest-level Green–Naghdi equations for a rotating shallow fluid layer, paying close attention to the flow structure at small spatial scales. We compare directly with the shallow-water equations and study the differences arising in their solutions. By recasting the equations into a form which both explicitly conserves Rossby–Ertel potential vorticity and represents the leading-order departure from geostrophic–hydrostatic balance, we are able to accurately describe both the ‘slow’ predominantly sub-inertial balanced dynamics and the ‘fast’ residual imbalanced dynamics. This decomposition has proved fruitful in studies of shallow-water dynamics but appears not to have been used before in studies of Green–Naghdi dynamics. Importantly, we find that this decomposition exposes a fundamental inconsistency in the Green–Naghdi equations for horizontal scales less than the mean fluid depth, scales for which the Green–Naghdi equations are supposed to more accurately model. Such scales exhibit pronounced activity compared to the shallow-water equations, and in particular spectra for certain fields like the divergence are flat or rising at high wavenumbers. This indicates a lack of convergence at small scales, and is also consistent with the poor convergence of total energy with resolution compared to the shallow-water equations. We suggest a mathematical reformulation of the Green–Naghdi equations which may improve convergence at small scales.
$H/L$. The shallow-water equations capture these effects to first order only, resulting in a relatively simple two-dimensional fluid-dynamical model for the layer horizontal velocity and depth. The Green–Naghdi equations, like the shallow-water equations, are two-dimensional fluid equations expressing momentum and mass conservation. There are different ‘levels’ of the Green–Naghdi equations of rapidly increasing complexity. In the present paper we focus on the behaviour of the lowest-level Green–Naghdi equations for a rotating shallow fluid layer, paying close attention to the flow structure at small spatial scales. We compare directly with the shallow-water equations and study the differences arising in their solutions. By recasting the equations into a form which both explicitly conserves Rossby–Ertel potential vorticity and represents the leading-order departure from geostrophic–hydrostatic balance, we are able to accurately describe both the ‘slow’ predominantly sub-inertial balanced dynamics and the ‘fast’ residual imbalanced dynamics. This decomposition has proved fruitful in studies of shallow-water dynamics but appears not to have been used before in studies of Green–Naghdi dynamics. Importantly, we find that this decomposition exposes a fundamental inconsistency in the Green–Naghdi equations for horizontal scales less than the mean fluid depth, scales for which the Green–Naghdi equations are supposed to more accurately model. Such scales exhibit pronounced activity compared to the shallow-water equations, and in particular spectra for certain fields like the divergence are flat or rising at high wavenumbers. This indicates a lack of convergence at small scales, and is also consistent with the poor convergence of total energy with resolution compared to the shallow-water equations. We suggest a mathematical reformulation of the Green–Naghdi equations which may improve convergence at small scales.
Please note a has been issued for this article.