Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T05:41:12.408Z Has data issue: false hasContentIssue false
  • English
  • Français

On the mechanism of the Gent–McWilliams instability of a columnar vortex in stratified rotating fluids

Published online by Cambridge University Press:  02 September 2015

Eunok Yim  and
Paul Billant
Eunok Yim*
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
Paul Billant
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In stably stratified and rotating fluids, an axisymmetric columnar vortex can be unstable to a special instability with an azimuthal wavenumber 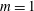$m=1$ which bends and slices the vortex into pancake vortices (Gent & McWilliams Geophys. Astrophys. Fluid Dyn., vol. 35 (1–4), 1986, pp. 209–233). This bending instability, called the ‘Gent–McWilliams instability’ herein, is distinct from the shear, centrifugal or radiative instabilities. The goals of the paper are to better understand the origin and properties of this instability and to explain why it operates only in stratified rotating fluids. Both numerical and asymptotic stability analyses of several velocity profiles have been performed for wide ranges of Froude number 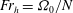$\mathit{Fr}_{h}={\it\Omega}_{0}/N$ and Rossby number 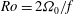$\mathit{Ro}=2{\it\Omega}_{0}/f$, where 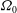${\it\Omega}_{0}$ is the angular velocity on the vortex axis, 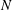$N$ the Brunt–Väisälä frequency and 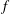$f$ the Coriolis parameter. Numerical analyses restricted to the centrifugally stable range show that the maximum growth rate of the Gent–McWilliams instability increases with 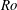$\mathit{Ro}$ and is independent of 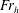$\mathit{Fr}_{h}$ for 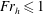$\mathit{Fr}_{h}\leqslant 1$. In contrast, when 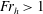$\mathit{Fr}_{h}>1$, the maximum growth rate decreases dramatically with 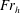$\mathit{Fr}_{h}$. Long axial wavelength asymptotic analyses for isolated vortices prove that the Gent–McWilliams instability is due to the destabilization of the long-wavelength bending mode by a critical layer at the radius 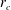$r_{c}$ where the angular velocity 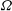${\it\Omega}$ is equal to the frequency 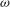${\it\omega}$: 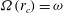${\it\Omega}(r_{c})={\it\omega}$. A necessary and sufficient instability condition valid for long wavelengths, finite Rossby number and 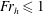$\mathit{Fr}_{h}\leqslant 1$ is that the derivative of the vertical vorticity of the basic vortex is positive at 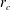$r_{c}$: 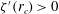${\it\zeta}^{\prime }(r_{c})>0$. Such a critical layer 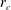$r_{c}$ exists for finite Rossby and Froude numbers because the real part of the frequency of the long-wavelength bending mode is positive instead of being negative as in a homogeneous non-rotating fluid (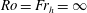$\mathit{Ro}=\mathit{Fr}_{h}=\infty$). When 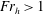$\mathit{Fr}_{h}>1$, the instability condition 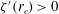${\it\zeta}^{\prime }(r_{c})>0$ is necessary but not sufficient because the destabilizing effect of the critical layer 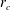$r_{c}$ is strongly reduced by a second stabilizing critical layer 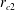$r_{c2}$ existing at the radius where the angular velocity is equal to the Brunt–Väisälä frequency. For non-isolated vortices, numerical results show that only finite axial wavenumbers are unstable to the Gent–McWilliams instability.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , pp. 5 - 44
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1970 Handbook of Mathematical Functions. Dover.Google Scholar
Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16, L1–L4.Google Scholar
Balmforth, N. J. 1999 Shear instability in shallow water. J. Fluid Mech. 387, 97–127.Google Scholar
Billant, P. 2010 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 1. General stability equations. J. Fluid Mech. 660, 354–395.Google Scholar
Billant, P., Colette, A. & Chomaz, J.-M.2004 Instabilities of a vortex pair in a stratified and rotating fluid. In Proceedings of the 21st International Congress of the International Union of Theoretical and Applied Mechanics, Varsovie, pp. 16–20.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.CrossRefGoogle Scholar
Billant, P. & Le Dizès, S. 2009 Waves on a columnar vortex in a strongly stratified fluid. Phys. Fluids 21, 106602.Google Scholar
Briggs, R. J., Daugherty, J. D. & Levy, R. H. 1970 Role of Landau damping in cross-field electron beams and inviscid shear flow. Phys. Fluids 13 (6), 421–432.CrossRefGoogle Scholar
Carnevale, G. F. & Kloosterziel, R. C. 1994 Emergence and evolution of triangular vortices. J. Fluid Mech. 259, 305–331.Google Scholar
Carton, X. J. & McWilliams, J. C. 1989 Barotropic and baroclinic instabilities of axisymmetric vortices in a quasigeostrophic model. In Mesoscale/Synoptic Coherent Structures in Geophysical Turbulence (ed. Nihoul, J. C. J. & Jamart, B. M.), Elsevier Oceanography Series, vol. 50, pp. 225–244. Elsevier.CrossRefGoogle Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 The Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.CrossRefGoogle Scholar
Flierl, G. R. 1988 On the instability of geostrophic vortices. J. Fluid Mech. 197, 349–388.Google Scholar
Gent, P. R. & McWilliams, J. C. 1986 The instability of barotropic circular vortices. Geophys. Astrophys. Fluid Dyn. 35 (1–4), 209–233.Google Scholar
Howard, L. N. & Gupta, A. S. 1962 On the hydrodynamic and hydromagnetic stability of swirling flows. J. Fluid Mech. 14 (3), 463–476.CrossRefGoogle Scholar
Hua, B. L. 1998 The internal barotropic instability of surface-intensified eddies. Part I: generalized theory for isolated eddies. J. Phys. Oceanogr. 18, 40–55.Google Scholar
Kelvin, L. 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Kloosterziel, R. C. & van Heijst, G. J. F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.CrossRefGoogle Scholar
Lahaye, N. & Zeitlin, V. 2015 Centrifugal, barotropic and baroclinic instabilities of isolated ageostrophic anticyclones in the two-layer rotating shallow water model and their nonlinear saturation. J. Fluid Mech. 762, 5–34.CrossRefGoogle Scholar
Le Dizès, S. 2000 Non-axisymmetric vortices in two-dimensional flows. J. Fluid Mech. 406, 175–198.CrossRefGoogle Scholar
Le Dizès, S. 2004 Viscous critical-layer analysis of vortex normal modes. Stud. Appl. Maths 112 (4), 315–332.CrossRefGoogle Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21 (9), 096602.CrossRefGoogle Scholar
Lin, C. C. 1955 The Theory of Hydrodynamics Stability. Cambridge University Press.Google Scholar
Michalke, A. & Timme, A. 1967 On inviscid instability of certain 2-dimensional vortex-type flows. J. Fluid Mech. 29 (4), 647–666.CrossRefGoogle Scholar
Montgomery, M. T. & Shapiro, L. J. 1995 Generalized Charney–Stern and Fjortoft theorems for rapidly rotating vortices. J. Atmos. Sci. 52 (16), 1829–1833.Google Scholar
Park, J. & Billant, P. 2012 Radiative instability of an anticyclonic vortex in a stratified rotating fluid. J. Fluid Mech. 707, 381–392.CrossRefGoogle Scholar
Park, J. & Billant, P. 2013 Instabilities and waves on a columnar vortex in a strongly stratified and rotating fluid. Phys. Fluids 25 (8), 086601.Google Scholar
Rayleigh, L. 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–70.Google Scholar
Rayleigh, L. 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93 (648), 148–154.Google Scholar
Reasor, P. D. & Montgomery, M. T. 2001 Three-dimensional alignment and corotation of weak, TC-like vortices via linear vortex rossby waves. J. Atmos. Sci. 58 (16), 2306–2330.Google Scholar
Reasor, P. D., Montgomery, M. T. & Grasso, L. D. 2004 A new look at the problem of tropical cyclones in vertical shear flow: vortex resiliency. J. Atmos. Sci. 61 (1), 3–22.Google Scholar
Riedinger, X. & Gilbert, A. D. 2014 Critical layer and radiative instabilities in shallow-water shear flows. J. Fluid Mech. 751, 539–569.CrossRefGoogle Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2010 Viscous stability properties of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.CrossRefGoogle Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Schecter, D. A., Dubin, D. H. E., Cass, A. C., Driscoll, C. F., Lansky, I. M. & O’Neil, T. M. 2000 Inviscid damping of asymmetries on a two-dimensional vortex. Phys. Fluids 12 (10), 2397–2412.Google Scholar
Schecter, D. A. & Montgomery, M. T. 2003 On the symmetrization rate of an intense geophysical vortex. Dyn. Atmos. Oceans 37, 55–88.Google Scholar
Schecter, D. A. & Montgomery, M. T. 2004 Damping and pumping of a vortex Rossby wave in a monotonic cyclone: critical layer stirring versus inertia–buoyancy wave emission. Phys. Fluids 16, 1334–1348.Google Scholar
Schecter, D. A. & Montgomery, M. T. 2006 Conditions that inhibit the spontaneous radiation of spiral inertia–gravity waves from an intense mesoscale cyclone. J. Atmos. Sci. 63, 435–456.Google Scholar
Schecter, D. A., Montgomery, M. T. & Reasor, P. D. 2002 A theory for the vertical alignment of a quasigeostrophic vortex. J. Atmos. Sci. 59 (2), 150–168.Google Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11 (3–4), 305–322.CrossRefGoogle Scholar
Widnall, S. E., Bliss, D. B. & Zalay, A. 1971 Theoretical and experimental study of the stability of a vortex pair. In Aircraft Wake Turbulence and Its Detection (ed. Olsen, A., Goldburg, J. H. & Rogers, M.), pp. 305–338. Springer.CrossRefGoogle Scholar