Published online by Cambridge University Press: 30 September 2016
The interaction of a hypersonic boundary layer on a flat plate with an impinging shock – an order of magnitude stronger than that required for incipient separation of the boundary layer – near sharp and blunt leading edges (with different bluntness radii from 2 to 6 mm) is investigated experimentally, complemented by numerical computations. The resultant separation bubble is of length comparable to the distance of shock impingement from the leading edge, rather than the boundary layer thickness at separation; it is termed large separation bubble. Experiments are performed in the IISc hypersonic shock tunnel HST-2 at nominal Mach numbers 5.88 and 8.54, with total enthalpies 1.26 and 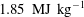 $1.85~\text{MJ}~\text{kg}^{-1}$ respectively. Schlieren flow visualization using a high-speed camera and surface pressure measurements using fast response sensors are the diagnostics. For the sharp leading edge case, the separation length was found to follow an inviscid scaling law according to which the scaled separation length
$1.85~\text{MJ}~\text{kg}^{-1}$ respectively. Schlieren flow visualization using a high-speed camera and surface pressure measurements using fast response sensors are the diagnostics. For the sharp leading edge case, the separation length was found to follow an inviscid scaling law according to which the scaled separation length 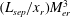 $(L_{sep}/x_{r})M_{er}^{3}$ is found to be linearly related to the reattachment pressure ratio
$(L_{sep}/x_{r})M_{er}^{3}$ is found to be linearly related to the reattachment pressure ratio  $p_{r}/p_{er}$; where
$p_{r}/p_{er}$; where 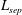 $L_{sep}$ is the measured separation length,
$L_{sep}$ is the measured separation length, 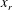 $x_{r}$ the distance of reattachment from the leading edge,
$x_{r}$ the distance of reattachment from the leading edge, 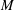 $M$ the Mach number,
$M$ the Mach number, 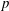 $p$ the static pressure and the subscripts
$p$ the static pressure and the subscripts  $r$ and
$r$ and  $e$ denote the conditions at the reattachment location and at the edge of the boundary layer at the shock impingement location respectively. However, for all the blunt leading edges
$e$ denote the conditions at the reattachment location and at the edge of the boundary layer at the shock impingement location respectively. However, for all the blunt leading edges 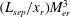 $(L_{sep}/x_{r})M_{er}^{3}$ was found to be a constant irrespective of Mach number and much smaller than the sharp leading edge cases. The possible contributions of viscous and non-viscous mechanisms towards the observed phenomena are explored.
$(L_{sep}/x_{r})M_{er}^{3}$ was found to be a constant irrespective of Mach number and much smaller than the sharp leading edge cases. The possible contributions of viscous and non-viscous mechanisms towards the observed phenomena are explored.
Present address: Marie Curie Fellow in Aerospace Engineering (Aerospace Sciences), School of Engineering, University of Glasgow, Glasgow G12 8QQ, UK.