Published online by Cambridge University Press: 30 September 2016
Droplets in turbulent flows behave differently from solid particles, e.g. droplets deform, break up, coalesce and have internal fluid circulation. Our objective is to gain a fundamental understanding of the physical mechanisms of droplet–turbulence interaction. We performed direct numerical simulations (DNS) of 3130 finite-size, non-evaporating droplets of diameter approximately equal to the Taylor length scale and with 5 % droplet volume fraction in decaying isotropic turbulence at initial Taylor-scale Reynolds number  $\mathit{Re}_{\unicode[STIX]{x1D706}}=83$. In the droplet-laden cases, we varied one of the following three parameters: the droplet Weber number based on the r.m.s. velocity of turbulence (
$\mathit{Re}_{\unicode[STIX]{x1D706}}=83$. In the droplet-laden cases, we varied one of the following three parameters: the droplet Weber number based on the r.m.s. velocity of turbulence (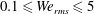 $0.1\leqslant \mathit{We}_{rms}\leqslant 5$), the droplet- to carrier-fluid density ratio (
$0.1\leqslant \mathit{We}_{rms}\leqslant 5$), the droplet- to carrier-fluid density ratio (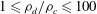 $1\leqslant \unicode[STIX]{x1D70C}_{d}/\unicode[STIX]{x1D70C}_{c}\leqslant 100$) or the droplet- to carrier-fluid viscosity ratio (
$1\leqslant \unicode[STIX]{x1D70C}_{d}/\unicode[STIX]{x1D70C}_{c}\leqslant 100$) or the droplet- to carrier-fluid viscosity ratio (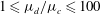 $1\leqslant \unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}\leqslant 100$). In this work, we derive the turbulence kinetic energy (TKE) equations for the two-fluid, carrier-fluid and droplet-fluid flow. These equations allow us to explain the pathways for TKE exchange between the carrier turbulent flow and the flow inside the droplet. We also explain the role of the interfacial surface energy in the two-fluid TKE equation through the power of the surface tension. Furthermore, we derive the relationship between the power of surface tension and the rate of change of total droplet surface area. This link allows us to explain how droplet deformation, breakup and coalescence play roles in the temporal evolution of TKE. Our DNS results show that increasing
$1\leqslant \unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}\leqslant 100$). In this work, we derive the turbulence kinetic energy (TKE) equations for the two-fluid, carrier-fluid and droplet-fluid flow. These equations allow us to explain the pathways for TKE exchange between the carrier turbulent flow and the flow inside the droplet. We also explain the role of the interfacial surface energy in the two-fluid TKE equation through the power of the surface tension. Furthermore, we derive the relationship between the power of surface tension and the rate of change of total droplet surface area. This link allows us to explain how droplet deformation, breakup and coalescence play roles in the temporal evolution of TKE. Our DNS results show that increasing 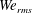 $\mathit{We}_{rms}$,
$\mathit{We}_{rms}$, 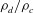 $\unicode[STIX]{x1D70C}_{d}/\unicode[STIX]{x1D70C}_{c}$ and
$\unicode[STIX]{x1D70C}_{d}/\unicode[STIX]{x1D70C}_{c}$ and 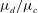 $\unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}$ increases the decay rate of the two-fluid TKE. The droplets enhance the dissipation rate of TKE by enhancing the local velocity gradients near the droplet interface. The power of the surface tension is a source or sink of the two-fluid TKE depending on the sign of the rate of change of the total droplet surface area. Thus, we show that, through the power of the surface tension, droplet coalescence is a source of TKE and breakup is a sink of TKE. For short times, the power of the surface tension is less than
$\unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}$ increases the decay rate of the two-fluid TKE. The droplets enhance the dissipation rate of TKE by enhancing the local velocity gradients near the droplet interface. The power of the surface tension is a source or sink of the two-fluid TKE depending on the sign of the rate of change of the total droplet surface area. Thus, we show that, through the power of the surface tension, droplet coalescence is a source of TKE and breakup is a sink of TKE. For short times, the power of the surface tension is less than 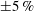 $\pm 5\,\%$ of the dissipation rate. For later times, the power of the surface tension is always a source of TKE, and its magnitude can be up to 50 % of the dissipation rate.
$\pm 5\,\%$ of the dissipation rate. For later times, the power of the surface tension is always a source of TKE, and its magnitude can be up to 50 % of the dissipation rate.
Instantaneous contours of kl = 1/2 (ρujuj ) in the x–z plane (1 < t < 3.5) for single-phase flow (case A, left) and droplet-laden flow (case C, right).
Instantaneous contours of εl = Re−1(Tij Sij ) in the x–z plane (1 < t < 3.5) for single-phase flow (case A, left) and droplet-laden flow (case C, right).
Instantaneous contours of εl = Re−1(Tij Sij ) in the x–z plane (1 < t < 3.5) for density ratio of 1 (ϕ = 1, case E, left) and 100 (ϕ = 100, case F, right).