Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T04:21:34.113Z Has data issue: false hasContentIssue false
  • English
  • Français

On the interaction of a compliant wall with a turbulent boundary layer

Published online by Cambridge University Press:  23 July 2020

Jin Wang ,
Subhra Shankha Koley  and
Joseph Katz Open the ORCID record for Joseph Katz [Opens in a new window]
Jin Wang
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Subhra Shankha Koley
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Joseph Katz*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

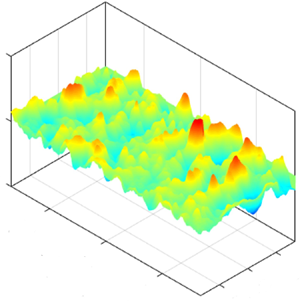
This study examines the interactions of a compliant wall with a turbulent boundary layer as the deformation scale increases from submicron to several wall units (δν). The friction velocity Reynolds number ranges between 1435 and 5179, and $E/\rho U_0^2$, where E is the Young modulus, varies from 59 to 2.4, $\rho $ is fluid density and $ U_0$ is free-stream velocity. Time-resolved Mach–Zehnder interferometry is used for measuring the spatial distribution of the surface deformation, and two-dimensional (2-D) particle image velocimetry for measuring the velocity in the inner part of the boundary layer. Reynolds stresses and two-point correlations are measured in the log layer. The deformation amplitude increases from 0.02δν at $E/\rho U_0^2 = 59$ to 3.6δν at $E/\rho U_0^2 = 2.4$. Wavenumber–frequency and 2-D spatial spectra show that the deformations consist of two modes: The first is an advected mode that travels downstream at 66 % of U0, has a lattice-like structure and a preferential spanwise alignment. The amplitude and frequency of this mode agree with the Chase (J. Acoust. Soc. Am., vol. 89, no. 6, 1991, pp. 2589–2596) and Benschop et al. (J. Fluid Mech., vol. 859, 2019, pp. 613–658) model predictions. The second mode is a streamwise-aligned wave that travels at the material shear speed (Ct = 7.85 m s−1) in the spanwise direction and has a wavelength of three times the compliant layer thickness. With decreasing $E/\rho U_0^2$, the velocity profiles in the boundary layer increasingly deviate from those of a rigid smooth wall. Yet, these deviations begin when the deformation is 0.02δν. The most prominent features are a sharp decrease in velocity at y < 10δν and an increase in the near-wall turbulence, both consistent, for matching $E/\rho U_0^2$, with the direct numerical simulation results of Rosti and Brandt (J. Fluid Mech., vol. 830, 2017, pp. 708–735).

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 899 , 25 September 2020 , A20
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1991 Particle-imaging techniques for experimental fluid mechanics. Annu. Rev. Fluid Mech. 23 (1), 261–304.CrossRefGoogle Scholar
Benjamin, T. B. 1960 Effects of a flexible boundary on hydrodynamic stability. J. Fluid Mech. 9, 513–532.CrossRefGoogle Scholar
Benjamin, T. B. 1963 The threefold classification of unstable disturbances in flexible surfaces bounding inviscid flows. J. Fluid Mech. 16, 436–450.CrossRefGoogle Scholar
Benschop, H. O. G., Greidanus, A. J., Delfos, R., Westerweel, J. & Breugem, W.-P. 2019 Deformation of a linear viscoelastic compliant coating in a turbulent flow. J. Fluid Mech. 859, 613–658.CrossRefGoogle Scholar
Blick, E. F. & Walters, R. R. 1968 Turbulent boundary-layer characteristics of compliant surfaces. J. Aircraft 5 (1), 11–16.CrossRefGoogle Scholar
Brereton, G. J. & Hwang, J. L. 1994 The spacing of streaks in unsteady turbulent wall-bounded flow. Phys. Fluids 6, 2446–2454.CrossRefGoogle Scholar
Burattini, P., Leonardi, S., Orlandi, P. & Antonia, R. A. 2008 Comparison between experiments and direct numerical simulations in a channel flow with roughness on one wall. J. Fluid Mech. 600, 403–426.CrossRefGoogle Scholar
Carpenter, P. W., Davies, C. & Lucey, A. D. 2000 Hydrodynamics and compliant walls: does the dolphin have a secret? Curr. Sci. 79 (6), 758–765.Google Scholar
Carpenter, P. W. & Garrad, A. D. 1985 The hydrodynamic stability of flows over Kramer-type compliant surfaces. Part 1. Tollmien–Schlichting instabilities. J. Fluid Mech. 155, 465–510.CrossRefGoogle Scholar
Carpenter, P. W. & Garrad, A. D. 1986 The hydrodynamic stability of flows over Kramer-type compliant surfaces. Part 2. Flow-induced surface instabilities. J. Fluid Mech. 170, 199–232.CrossRefGoogle Scholar
Castellini, P., Martarelli, M. & Tomasini, E. P. 2006 Laser Doppler vibrometry: development of advanced solutions answering to technology's needs. Mech. Syst. Signal Process. 20, 1265–1285.CrossRefGoogle Scholar
Charruault, F., Greidanus, A. & Westerweel, J. 2018 A dot tracking algorithm to measure free surface deformations. In 18th Intl Symp. on Flow Visualization, Zurich, Switzerland. ETH Zurich.Google Scholar
Chase, D. M. 1991 Generation of fluctuating normal stress in a viscoelastic layer by surface shear stress and pressure as in turbulent boundary-layer flow. J. Acoust. Soc. Am. 89 (6), 2589–2596.CrossRefGoogle Scholar
Choi, K.-S., Yang, X., Clayton, B. R., Glover, E. J., Atlar, M., Semenov, B. N. & Kulik, V. M. 1997 Turbulent drag reduction using compliant surfaces. Proc. R. Soc. Lond. A 453, 2229–2240.CrossRefGoogle Scholar
Djenidi, L., Antonia, R. A., Amielh, M. & Anselmet, F. 2008 A turbulent boundary layer over a two-dimensional rough wall. Exp. Fluids 44, 37–47.CrossRefGoogle Scholar
Duncan, J. H. 1986 The response of an incompressible, viscoelastic coating to pressure fluctuations in a turbulent boundary layer. J. Fluid Mech. 171, 339–363.CrossRefGoogle Scholar
Endo, T. & Himeno, R. 2002 Direct numerical simulation of turbulent flow over a compliant surface. J. Turbul. 3, 1–10.CrossRefGoogle Scholar
Fisher, D. H. & Blick, E. F. 1966 Turbulent damping by flabby skins. J. Aircraft 3 (2), 163–164.CrossRefGoogle Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26, 101305.CrossRefGoogle Scholar
Gad-El-Hak, M. 1986 The response of elastic and visco-elastic surfaces to a turbulent boundary layer. Trans. ASME E: J. Appl. Mech. 53, 206–212.CrossRefGoogle Scholar
Gad-El-Hak, M., Blackwelder, R. F. & Riley, J. J. 1984 On the interaction of compliant coatings with boundary layer flows. J. Fluid Mech. 140, 257–280.CrossRefGoogle Scholar
Gao, J. & Katz, J. 2018 Self-calibrated microscopic dual-view tomographic holography for 3D flow measurements. Opt. Express 26, 16708–16725.CrossRefGoogle ScholarPubMed
Ghiglia, D. C., Mastin, G. A. & Romero, L. A. 1987 Cellular-automata method for phase unwrapping. J. Opt. Soc. Am. A 4, 267–280.CrossRefGoogle Scholar
Goldstein, R. M., Zebker, H. A. & Werner, C. L. 1988 Radar interferometry: two-dimensional phase unwrapping. Radio Science 23, 713–720.CrossRefGoogle Scholar
Goody, M. 2004 Empirical spectral model of surface pressure fluctuations. AIAA J. 42 (9), 1788–1794.CrossRefGoogle Scholar
Grant, I. 1997 Particle image velocimetry: a review. Proc. Inst. Mech. Engrs C 211, 55–76.Google Scholar
Hansen, R. J. & Hunston, D. L. 1974 An experimental study of turbulent flows over compliant surfaces. J. Sound Vib. 34, 297–308.CrossRefGoogle Scholar
Hansen, R. J. & Hunston, D. L. 1983 Fluid-property effects on flow-generated waves on a compliant surface. J. Fluid Mech. 133, 161–177.CrossRefGoogle Scholar
Harris, G. L. & Lissaman, P. B. S. 1969 Turbulent skin friction on compliant surfaces. AIAA J. 7 (8), 1625–1627.Google Scholar
Hartman, B., Lee, G. F. & Lee, J. D. 1994 Loss factor height and widths for polymer relaxations. J. Acoust. Soc. Am. 95 (1), 226–233.CrossRefGoogle Scholar
Hess, D. E., Peattie, R. A. & Schwarz, W. H. 1993 A noninvasive method for the measurement of flow-induced surface displacement of a compliant surface. Exp. Fluids 14, 78–84.CrossRefGoogle Scholar
Hong, J., Katz, J., Meneveau, C. & Schultz, M. P. 2012 Coherent structures and associated subgrid-scale energy transfer in a rough-wall turbulent channel flow. J. Fluid Mech. 712, 92–128.CrossRefGoogle Scholar
Hong, J., Katz, J. & Schultz, M. P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.CrossRefGoogle Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.CrossRefGoogle Scholar
Jimenez, J. 2003 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Joshi, P., Liu, X. & Katz, J. 2014 Effect of mean and fluctuating pressure gradients on boundary layer turbulence. J. Fluid Mech. 748, 36–84.CrossRefGoogle Scholar
Kim, E. & Choi, H. 2014 Space-time characteristics of a compliant wall in a turbulent channel flow. J. Fluid Mech. 756, 30–53.CrossRefGoogle Scholar
Kramer, M. O. 1957 Boundary-layer stabilization by distributed damping. J. Aero. Sci. 24, 459–460.Google Scholar
Kramer, M. O. 1962 Boundary-layer stabilization by distributed damping. Naval Engrs J. 74 (2), 341–348.CrossRefGoogle Scholar
Landahl, M. T. 1962 On the stability of a laminar incompressible boundary layer over a flexible surface. J. Fluid Mech. 13, 609–632.CrossRefGoogle Scholar
Lee, T., Fisher, M. & Schwarz, W. H. 1993 a Investigation of the stable interaction of a passive compliant surface with a turbulent boundary layer. J. Fluid Mech. 257, 373–401.CrossRefGoogle Scholar
Lee, T., Fisher, M. & Schwarz, W. H. 1993 b The measurement of flow-induced surface displacement on a compliant surface by optical holographic interferometry. Exp. Fluids 14, 159–168.CrossRefGoogle Scholar
Lee, S. H. & Sung, H. J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.CrossRefGoogle Scholar
Li, Y., Chen, H. & Katz, J. 2017 Measurements and characterization of turbulence in the tip region of an axial compressor rotor. Trans. ASME: J. Turbomach. 139, 121003.Google Scholar
Ling, H., Srinivasan, S., Golovin, K., McKinley, G. H., Tuteja, A. & Katz, J. 2016 High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces. J. Fluid Mech. 801, 670–703.CrossRefGoogle Scholar
Lucey, A. D. & Carpenter, P. W. 1992 A numerical simulation of the interaction of a compliant wall and inviscid flow. J. Fluid Mech. 234, 121–146.CrossRefGoogle Scholar
McMichael, J. M., Klebanoff, P. S. & Mease, N. E. 1980 Experimental investigation of drag on a compliant surface. In Viscous Flow Drag Reduction (ed. Hough, G. R.), vol. 72, pp. 410–438. AIAA.Google Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8, 1406–1416.CrossRefGoogle Scholar
Moisy, F., Rabaud, M. & Salsac, K. 2009 A synthetic Schlieren method for the measurement of the topography of a liquid interface. Exp. Fluids 46 (6), 1021–1063.CrossRefGoogle Scholar
Mooney, M. 1940 A theory of large elastic deformation. J. Appl. Phys. 11 (9), 582–592.CrossRefGoogle Scholar
Naka, Y., Stanislas, M., Foucaut, J., Coudert, S., Laval, J. & Obi, S. 2015 Space–time pressure–velocity correlations in a turbulent boundary layer. J. Fluid Mech. 771, 624–675.CrossRefGoogle Scholar
Palchesko, R. N., Zhang, L., Yan, S. & Feinberg, A. W. 2012 Development of polydimethylsiloxane substrates with tunable elastic modulus to study cell mechanobiology in muscle and nerve. PLoS ONE 7 (12), e51499.CrossRefGoogle ScholarPubMed
Panton, R. L., Goldamn, A. L., Lowery, R. L. & Reischman, M. M. 1980 Low- frequency pressure fluctuations in axisymmetric turbulent boundary layers. J. Fluid Mech. 97, 299–319.CrossRefGoogle Scholar
Perry, A. E., Lim, K. L. & Henbest, S. M. 1987 An experimental study of the turbulence structure in smooth- and rough-wall boundary layers. J. Fluid Mech. 177, 437–466.CrossRefGoogle Scholar
Piomelli, U. 2019 Recent advances in the numerical simulation of rough-wall boundary layers. Phys. Chem. Earth 113, 63–72.CrossRefGoogle Scholar
Rivlin, R. S. 1948 Large elastic deformations of isotropic materials. IV. Further developments of the general theory. Phil. Trans. R. Soc. Lond. A 241 (835), 379–397.Google Scholar
Rosti, M. E. & Brandt, L. 2017 Numerical simulation of turbulent channel flow over a viscous hyper-elastic wall. J. Fluid Mech. 830, 708–735.CrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2006 Digital holographic microscope for measuring three-dimensional particle distributions and motions. Appl. Opt. 45, 3893–3901.CrossRefGoogle ScholarPubMed
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.CrossRefGoogle Scholar
Tabatabai, H., Oliver, D. E., Rohrbaugh, J. W. & Papadopoulos, C. 2013 Novel applications of laser Doppler vibration measurements to medical imaging. Sens. Imaging 14, 13–28.CrossRefGoogle ScholarPubMed
Talapatra, S. & Katz, J. 2012 Coherent structures in the inner part of a rough-wall channel flow resolved using holographic PIV. J. Fluid Mech. 711, 161–170.CrossRefGoogle Scholar
Tan, D., Li, Y., Wilkes, I., Vagnonii, E., Miorini, R. L. & Katz, J. 2015 Experimental investigation of the role of large scale cavitating vortical structures in performance breakdown of an axial waterjet pump. Trans. ASME: J. Fluids Engng 137 (11), 111301.Google Scholar
Tsuji, Y., Fransson, J., Alfredsson, P. & Johansson, A. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.CrossRefGoogle Scholar
Wang, Z., Yeo, K. S. & Khoo, B. C. 2006 On two-dimensional linear waves in Blasius boundary layer over viscoelastic layers. Eur. J. Mech. (B/Fluids) 25, 33–58.CrossRefGoogle Scholar
Wang, J., Zhang, C. & Katz, J. 2019 GPU-based, parallel-line, omni-directional integration of measured pressure gradient field to obtain the 3D pressure distribution. Exp. Fluids 60, 58.CrossRefGoogle Scholar
Westerweel, J., Geelhoed, P. F. & Lindken, R. 2004 Single-pixel resolution ensemble correlation for micro-PIV applications. Exp. Fluids 37, 375–384.CrossRefGoogle Scholar
Xia, Q. J., Huang, W. X. & Xu, C. X. 2017 Direct numerical simulation of turbulent boundary layer over a compliant wall. J. Fluids Struct. 71, 126–142.CrossRefGoogle Scholar
Xu, S., Rempfer, D. & Lumley, J. 2003 Turbulence over a compliant surface: numerical simulation and analysis. J. Fluid Mech. 478, 11–34.CrossRefGoogle Scholar
Zhang, C., Miorini, R. & Katz, J. 2015 Integrating Mach–Zehnder interferometry with TPIV to measure the time - resolved deformation of a compliant wall along with the 3D velocity field in a turbulent channel flow. Exp. Fluids 56, 1–22.CrossRefGoogle Scholar
Zhang, C., Wang, J., Blake, W. & Katz, J. 2017 Deformation of a compliant wall in a turbulent channel flow. J. Fluid Mech. 823, 345–390.CrossRefGoogle Scholar

Wang et al. supplementary movie 1

Spatially detrended deformation of a compliant wall at ${\it U_0}=1.2\;m/s$, and ${\it E/\rho U_0^2} = 59.0$
Download Wang et al. supplementary movie 1(Video)
Video 9.7 MB

Wang et al. supplementary movie 2

Spatially detrended deformation of a compliant wall at ${\it U_0}=3.2\;m/s$, and ${\it E/\rho U_0^2} = 8.3$
Download Wang et al. supplementary movie 2(Video)
Video 10.3 MB

Wang et al. supplementary movie 3

Spatially detrended deformation of a compliant wall at ${\it U_0}=5.3\;m/s$, and ${\it E/\rho U_0^2} = 3.0$
Download Wang et al. supplementary movie 3(Video)
Video 10.3 MB