Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T05:11:04.600Z Has data issue: false hasContentIssue false
  • English
  • Français

On the free-surface flow of very steep forced solitary waves

Published online by Cambridge University Press:  13 December 2013

Stephen L. Wade ,
Benjamin J. Binder ,
Trent W. Mattner  and
James P. Denier
Stephen L. Wade*
Affiliation:
School of Mathematical Sciences, The University of Adelaide, Adelaide, SA 5005, Australia
Benjamin J. Binder
Affiliation:
School of Mathematical Sciences, The University of Adelaide, Adelaide, SA 5005, Australia
Trent W. Mattner
Affiliation:
School of Mathematical Sciences, The University of Adelaide, Adelaide, SA 5005, Australia
James P. Denier
Affiliation:
Department of Engineering Science, The University of Auckland, Auckland 1142, New Zealand
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

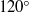The free-surface flow of very steep forced and unforced solitary waves is considered. The forcing is due to a distribution of pressure on the free surface. Four types of forced solution are identified which all approach the Stokes-limiting configuration of an included angle of $12{0}^{\circ } $ and a stagnation point at the wave crests. For each type of forced solution the almost-highest wave does not contain the most energy, nor is it the fastest, similar to what has been observed previously in the unforced case. Nonlinear solutions are obtained by deriving and solving numerically a boundary integral equation. A weakly nonlinear approximation to the flow problem helps with the identification and classification of the forced types of solution, and their stability.

JFM classification

Waves/Free-surface Flows: Channel flow Waves/Free-surface Flows: Solitary waves Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 739 , 25 January 2014 , pp. 1 - 21
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akylas, T. R. 1984 On the excitation of long nonlinear water waves by a moving pressure distribution. J. Fluid Mech. 141, 455–466.CrossRefGoogle Scholar
Allgower, E. L. & Georg, K. 1990 Numerical Continuation Methods: An Introduction. Springer.Google Scholar
Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
Binder, B. J., Dias, F. & Vanden-Broeck, J.-M. 2005 Forced solitary waves and fronts past submerged obstacles. Chaos 15, 037106.Google Scholar
Binder, B. J. & Vanden-Broeck, J. -M. 2007 The effect of disturbances on the flow under a sluice gate and past an inclined plate. J. Fluid Mech. 576, 475–490.Google Scholar
Binder, B. J., Vanden-Broeck, J.-M. & Dias, F. 2008 Influence of rapid changes in a channel bottom on free-surface flows. IMA J. Appl. Maths. 73, 254–273.CrossRefGoogle Scholar
Byatt-Smith, J. G. B. & Longuet-Higgins, M. S. 1976 On the speed and profile of steep solitary waves. Proc. R. Soc. A 350, 175–189.Google Scholar
Camassa, R. & Wu, T. 1991 Stability of forced steady solitary waves. Phil. Trans. R. Soc. Lond. 337, 429–466.Google Scholar
Chardard, F., Dias, F., Nguyen, H. Y. & Vanden-Broeck, J. -M. 2011 Stability of some stationary solutions to the forced KdV equation with one or two bumps. J. Engng Maths 70, 175–189.Google Scholar
Cole, S. L. 1985 Transient waves produced by flow past a bump. Wave Motion 7, 579–587.CrossRefGoogle Scholar
Dias, F. & Vanden-Broeck, J. -M. 1989 Open channel flows with submerged obstructions. J. Fluid Mech. 206, 155–170.Google Scholar
Ee, B. K., Grimshaw, R. H. J., Zhang, D.-H. & Chow, K. W. 2010 Steady transcritical flow over a hole: parametric map of solutions of the forced Korteweg–de Vries equation. Phys. Fluids 22, 056602.Google Scholar
Ee, B. K., Grimshaw, R. H. J., Chow, K. W. & Zhang, D.-H. 2011 Steady transcritical flow over an obstacle: parametric map of solutions of the forced extended Korteweg–de Vries equation. Phys. Fluids 23, 046602.Google Scholar
Gradshtein, I. S., Ryzhik, I. M. & Jeffrey, A. 2000 Table of Integrals, Series, and Products, 6th edn. Academic.Google Scholar
Grimshaw, R. H. J. & Smyth, N. 1986 Resonant flow of a stratified fluid over topography. J. Fluid Mech. 169, 429–464.CrossRefGoogle Scholar
Grimshaw, R. H. J., Zhang, D.-H. & Chow, K. W. 2007 Generation of solitary waves by transcritical flow over a step. J. Fluid Mech. 587, 235–254.CrossRefGoogle Scholar
Havelock, T. H. 1919 Periodic irrotational waves of finite amplitude. Proc. R. Soc. London Ser. A 95, 38–51.Google Scholar
Hunter, J. K. & Vanden-Broeck, J. -M. 1983 Accurate computations for steep solitary waves. J. Fluid Mech. 136, 63–71.CrossRefGoogle Scholar
Kataoka, T. 2006 On the superharmonic instability of surface gravity waves on fluid of finite depth. J. Fluid Mech. 547, 175–184.Google Scholar
Korteweg, de Vries 1895 On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. 5, xxxix. 422.Google Scholar
Levi-Civita, T. 1925 Détermination rigoureuse des ondes permanentes d’ampleur finie. Math. Ann. 93, 264–314.CrossRefGoogle Scholar
Lim, T. H. & Smith, A. C. 1978 A Cauchy integral-equation method for the numerical solution of the steady water–wave problem. J. Engng. Maths. 12, 325–340.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Cleaver, R. P. 1994 Crest instabilities of gravity waves. Part 1. The almost-highest wave. J. Fluid Mech. 258, 115–129.Google Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1977 Theory of the almost-highest wave: the inner solution. J. Fluid Mech. 80, 721–741.Google Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1996 Asymptotic theory for the almost-highest solitary wave. J. Fluid Mech. 317, 1–19.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Fenton, J. D. 1974 On the mass, momentum, energy and circulation of a solitary Wave. II. Proc. R. Soc. A 340, 471–493.Google Scholar
Longuet-Higgins, M. S. & Tanaka, M. 1997 On the crest instabilities of steep surface waves. J. Fluid Mech. 336, 51–68.CrossRefGoogle Scholar
Lustri, C. J., McCue, S. W. & Binder, B. J. 2012 Free surface flow past topography: a beyond-all-orders approach. Eur. J. Appl. Maths 23, 441–467.Google Scholar
Maklakov, D. V. 2002 Almost-highest gravity waves on water of finite depth. Eur. J. Appl. Maths 13, 67–93.CrossRefGoogle Scholar
Malomed, B. A. 1988 Interaction of a moving dipole with a soliton in the KdV equation. Physica D 32, 393–408.CrossRefGoogle Scholar
McLeod, J. B. 1997 The Stokes and Krasovskii conjectures for the wave of greatest height. Stud. Appl. Maths 98, 311–333.CrossRefGoogle Scholar
Miles, J. 1986 Stationary, transcritical channel flow. J. Fluid Mech. 162, 489–499.Google Scholar
Shen, S. S.-P. 1993 A Course on Nonlinear Waves. Kluwer Academic.Google Scholar
Shen, S. S-P., Shen, M. C. & Sun, S. M. 1989 A model equation for steady surface waves over a bump. J. Engng Maths 23, 315–323.Google Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Stokes, G. G. 1880 Supplement to a paper on the theory of oscillatory waves. Math. Phys. Papers 1, 197–229.Google Scholar
Schwartz, L. W. & Fenton, J. D. 1982 Strongly nonlinear waves. Annu. Rev. Fluid Mech. 14, 39–60.Google Scholar
Tanaka, M. 1986 The stability of solitary waves. Phys. Fluids 29, 650–655.CrossRefGoogle Scholar
Williams, J. M. 1981 Limiting gravity waves in water of finite depth. Phil. Trans. R. Soc. Lond. A 302, 139–188.Google Scholar
Wu, T. 1987 Generation of upstream advancing solitons by moving disturbances. J. Fluid Mech. 184, 75–99.Google Scholar
Vanden-Broeck, J. -M. 1986 Steep gravity waves: Havelock’s method revisited. Phys. Fluids 29, 3084–3085.Google Scholar
Vanden-Broeck, J. -M. 1987 Free-surface flow over an obstruction in a channel. Phys. Fluids 30, 2315–2317.Google Scholar
Vanden-Broeck, J. -M. 1997 Numerical calculations of the free-surface flow under a sluice gate. J. Fluid Mech. 330, 339–347.Google Scholar
Vanden-Broeck, J. -M. & Keller, J. B. 1989 Surfing on solitary waves. J. Fluid Mech. 198, 115–125.CrossRefGoogle Scholar