Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T13:47:45.944Z Has data issue: false hasContentIssue false
  • English
  • Français

On the energetics of a two-layer baroclinic flow

Published online by Cambridge University Press:  08 March 2017

Thibault Jougla Open the ORCID record for Thibault Jougla [Opens in a new window]  and
David G. Dritschel
Thibault Jougla*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
David G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The formation, evolution and co-existence of jets and vortices in turbulent planetary atmospheres is examined using a two-layer quasi-geostrophic 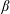$\unicode[STIX]{x1D6FD}$-channel shallow-water model. The study in particular focuses on the vertical structure of jets. Following Panetta & Held (J. Atmos. Sci., vol. 45 (22), 1988, pp. 3354–3365), a vertical shear arising from latitudinal heating variations is imposed on the flow and maintained by thermal damping. Idealised convection between the upper and lower layers is implemented by adding cyclonic/anti-cyclonic pairs, called hetons, to the flow, though the qualitative flow evolution is evidently not sensitive to this or other small-scale stochastic forcing. A very wide range of simulations have been conducted. A characteristic simulation which exhibits alternation between two different phases, quiescent and turbulent, is examined in detail. We study the energy transfers between different components and modes, and find the classical picture of barotropic/baroclinic energy transfers to be too simplistic. We also discuss the dependence on thermal damping and on the imposed vertical shear. Both have a strong influence on the flow evolution. Thermal damping is a major factor affecting the stability of the flow while vertical shear controls the number of jets in the domain, qualitatively through the Rhines scale 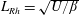$L_{Rh}=\sqrt{U/\unicode[STIX]{x1D6FD}}$.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Geophysical and Geological Flows: Geostrophic turbulence Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 586 - 618
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbic, B. K. & Flierl, G. R. 2004 Baroclinically unstable geostrophic turbulence in the limits of strong and weak bottom ekman friction: application to midocean eddies. J. Phys. Oceanogr. 34 (10), 2257–2273.Google Scholar
Atkinson, D. H., Pollack, J. B. & Seiff, A. 1998 The galileo probe doppler wind experiment: measurement of the deep zonal winds on jupiter. J. Geophys. Res. 103 (E10), 22911–22928.CrossRefGoogle Scholar
Berloff, P., Karabasov, S., Farrar, J. T. & Kamenkovich, I. 2011 On latency of multiple zonal jets in the oceans. J. Fluid Mech. 686, 534–567.Google Scholar
Busse, F. H. 1970 Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 44 (03), 441–460.CrossRefGoogle Scholar
Busse, F. H. 1976 A simple model of convection in the jovian atmosphere. Icarus 29, 255–260.Google Scholar
Carton, X. 2001 Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 22 (3), 179–263.Google Scholar
Cho, J. Y.-K. & Polvani, L. M. 1996 The emergence of jets and vortices in freely-evolving shallow-water turbulence on a sphere. Phys. Fluids 8, 1531–1552.Google Scholar
Dowling, T. E. 1995 Dynamics of jovian atmospheres. Annu. Rev. Fluid Mech. 27 (1), 293–334.CrossRefGoogle Scholar
Dowling, T. E. & Ingersoll, A. P. 1988 Potential vorticity and layer thickness variations in the flow around jupiter’s great red spot and white oval bc. J. Atmos. Sci. 45 (8), 1380–1396.Google Scholar
Dowling, T. E. & Ingersoll, A. P. 1989 Jupiter’s great red spot as a shallow water system. J. Atmos. Sci. 46, 3256–3278.2.0.CO;2>CrossRefGoogle Scholar
Dritschel, D. G. & Fontane, J. 2010 The combined Lagrangian advection method. J. Comput. Phys. 229, 5408–5417.Google Scholar
Dritschel, D. G. & Mcintyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.Google Scholar
Dritschel, D. G. & Tobias, S. M. 2012 Two-dimensional magnetohydrodynamic turbulence in the small magnetic prandtl number limit. J. Fluid Mech. 703, 85–98.CrossRefGoogle Scholar
Esler, J. G. 2008 The turbulent equilibration of an unstable baroclinic jet. J. Fluid Mech. 599, 241–268.CrossRefGoogle Scholar
Feldstein, S. B. & Held, I. M. 1989 Barotropic decay of baroclinic waves in a two-layer beta-plane model. J. Atmos. Sci. 46 (22), 3416–3430.Google Scholar
Fontane, J. & Dritschel, D. G. 2009 The hypercasl algorithm: a new approach to the numerical simulation of geophysical flows. J. Comput. Phys. 228 (17), 6411–6425.Google Scholar
Fu, L. L. & Flierl, G. R. 1980 Nonlinear energy and enstrophy transfers in a realistically stratified ocean. Dyn. Atmos. Oceans 4 (4), 219–246.Google Scholar
Ingersoll, A. P., Dowling, T. E., Gierasch, P. J., Orton, G. S., Read, P. L., Sanchez-Lavega, A., Showman, A. P., Simon-Miller, A. A. & Vasavada, A. R. 2004 Dynamics of Jupiter’s Atmosphere. pp. 105–128. Cambridge University Press.Google Scholar
James, I. N. 1987 Suppression of baroclinic instability in horizontally sheared flows. J. Atmos. Sci. 44 (24), 3710–3720.Google Scholar
Kamenkovich, I., Berloff, P. & Pedlosky, J. 2009 Role of eddy forcing in the dynamics of multiple zonal jets in a model of the north atlantic. J. Phys. Oceanogr. 39 (6), 1361–1379.CrossRefGoogle Scholar
Kaspi, Y. & Flierl, G. R. 2007 Formation of jets by baroclinic instability on gas planet atmospheres. J. Atmos. Sci. 64 (9), 3177–3194.Google Scholar
Kaspi, Y., Flierl, G. R. & Showman, A. P. 2009 The deep wind structure of the giant planets: results from an anelastic general circulation model. Icarus 202 (2), 525–542.Google Scholar
Limaye, S. S. 1986 Jupiter: New estimates of the mean zonal flow at the cloud level. Icarus 65 (2), 335–352.Google Scholar
Liu, J. & Schneider, T. 2010 Mechanisms of jet formation on the giant planets. J. Atmos. Sci. 67 (11), 3652–3672.Google Scholar
Marcus, P. S. 1993 Jupiter’s great red spot and other vortices. Annu. Rev. Astron. Astrophys. 31, 523–573.CrossRefGoogle Scholar
Maximenko, N. A., Bang, B. & Sasaki, H. 2005 Observational evidence of alternating zonal jets in the world ocean. Geophys. Res. Lett. 32, L12607.CrossRefGoogle Scholar
Mohebalhojeh, A. R. & Dritschel, D. G. 2004 Contour-advective semi-lagrangian algorithms for many-layer primitive-equation models. Q. J. R. Meteorol. Soc. 130 (596), 347–364.Google Scholar
Panetta, R. L. & Held, I. M. 1988 Baroclinic eddy fluxes in a one-dimensional model of quasi-geostrophic turbulence. J. Atmos. Sci. 45 (22), 3354–3365.Google Scholar
Phillips, N. 1951 A simple three-dimensional model for the study of large-scale extra-tropical flow patterns. J. Meteorol. 8, 381–394.Google Scholar
Porco, C. C., West, R. A., McEwen, A., Del Genio, A. D., Ingersoll, A. P., Thomas, P., Squyres, S., Dones, L., Murray, C. D., Johnson, T. V. et al. 2003 Cassini imaging of jupiter’s atmosphere, satellites, and rings. Science 299 (5612), 1541–1547.Google Scholar
Rhines, P. B. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–443.Google Scholar
Rogers, J. H. 1995 The Giant Planet Jupiter. Cambridge University Press.Google Scholar
Sachs, A. 1974 Babylonian observational astronomy. Phil. Trans. R. Soc. Lond. A 276 (1257), 43–50.Google Scholar
Scott, R. K. 2007 Non-robustness of the two-dimensional turbulent inverse cascade. Phys. Rev. E 75, 046301.Google Scholar
Scott, R. K. & Dritschel, D. G. 2012 The structure of zonal jets in geostrophic turbulence. J. Fluid Mech. 711, 576–598.Google Scholar
Showman, A. P. 2007 Numerical simulations of forced shallow-water turbulence: effects of moist convection on the large-scale circulation of Jupiter and Saturn. J. Atmos. Sci. 64 (9), 3132–3157.Google Scholar
Simon, A. A., Wong, M. H. & Orton, G. S. 2015 First results from the hubble opal program: Jupiter in 2015. Astrophys. J. 812 (1), 55.Google Scholar
Smith, K. & Vallis, G. K. 2002 The scales and equilibration of midocean eddies. J. Phys. Oceanogr. 32 (6), 1699–1720.Google Scholar
Spiga, A., Guerlet, S., Meurdesoif, Y., Indurain, M., Millour, E., Dubos, T., Sylvestre, M., Leconte, J. & Fouchet, T. 2015 Waves and eddies simulated by high-resolution global climate modeling of saturn’s troposphere and stratosphere. In EPSC 2015, vol. 10, p. 881.Google Scholar
Thompson, A. F. & Young, W. R. 2007 Two-layer baroclinic eddy heat fluxes: zonal flows and energy balance. J. Atmos. Sci. 64, 3214–3231.Google Scholar
Thomson, S. I. & Mcintyre, M. E. 2016 Jupiter’s unearthly jets: a new turbulent model exhibiting statistical steadiness without large-scale dissipation. J. Atmos. Sci. 73 (3), 1119–1141.Google Scholar
Thorncroft, C. D., Hoskins, B. J. & Mcintyre, M. E. 1993 Two paradigms of baroclinic-wave life-cycle behaviour. Q. J. R. Meteorol. Soc. 119, 17–55.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Venaille, A., Nadeau, L. P. & Vallis, G. K. 2014 Ribbon turbulence. Phys. Fluids 26 (12), 126605.Google Scholar
Williams, G. P. 1978 Planetary circulations: 1. Barotropic representation of Jovian and terrestrial turbulence. J. Atmos. Sci. 35, 1399–1424.Google Scholar

Jougla et al. supplementary movie

This movie exhibits the upper layer flow (on the top) and the lower layer flow (on the bottom) corresponding to figures 3 and 4, but from $t=3500$ to $t=4500$. Left: normalised latitude $2y/\pi$ vs zonally-averaged zonal velocity $\bar{u}_i(y,t)$. Centre: PV field $q_i(x,y,t)$ over the entire domain. Right: equivalent latitude $y_e( \tilde{q},t)$ vs normalised PV $ \tilde{q}=(q-q_{\mathsf{min}})/(q_{\mathsf{max}}-q_{\mathsf{min}})$.

Download Jougla et al. supplementary movie(Video)
Video 8.1 MB

Jougla et al. supplementary movie

This movie exhibits the upper layer flow (on the top) and the lower layer flow (on the bottom) corresponding to figure 5, but from $t=9000$ to $t=10000$. Left: normalised latitude $2y/\pi$ vs zonally-averaged zonal velocity $\bar{u}_i(y,t)$. Centre: PV field $q_i(x,y,t)$ over the entire domain. Right: equivalent latitude $y_e( \tilde{q},t)$ vs normalised PV $ \tilde{q}=(q-q_{\mathsf{min}})/(q_{\mathsf{max}}-q_{\mathsf{min}})$.

Download Jougla et al. supplementary movie(Video)
Video 8.9 MB