Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-06T10:34:14.195Z Has data issue: false hasContentIssue false
  • English
  • Français

On the effects of finite-rate carbon/oxygen chemistry on supersonic jet instability

Published online by Cambridge University Press:  17 October 2012

Luca Massa  and
Prashaanth Ravindran
Luca Massa*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Texas at Arlington, Arlington, TX 76019, USA
Prashaanth Ravindran
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Texas at Arlington, Arlington, TX 76019, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The instability of high-temperature jets is studied because of its importance to the analysis of gas-turbine engine exhaust flow, shock–shock interaction and bypass transition. The focus is on fluid–chemistry coupling, where the chemical time scales are supported by both reactive and inelastic molecular processes. The former are associated with dissociation/exchange reactions, while the latter are associated with transfers of vibrational quanta. The interaction affects both the instability growth rate and acoustic feedback by sustaining thermo-acoustic damping. Resonance conditions are identified as those that yield the maximum damping against the Damköhler number. The main results of the present study are the explanation of the dichotomy between vortical and acoustic modes in relation to the thermo-acoustic damping, and the analysis of the resonance condition as it depends on the physico-chemical properties of carbon/oxygen mixtures. The ability of a mode to support thermo-acoustic damping is related to the local convective Mach number of its most amplified frequency, and thus to the phenomenon of acoustic trapping in the jet core. Regarding the second issue, carbon dioxide acts as the best damper at low jet temperatures ${T}_{j} \approx 1000~\mathrm{K} $, where the vibrational relaxation is the main chemical scale, and up to 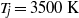${T}_{j} = 3500~\mathrm{K} $ because its reactive chemistry resonates with the fluid fluctuation at a lower temperature than the dissociation of 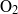${\mathrm{O} }_{2} $. At higher temperatures, oxygen is the best damper because of the larger endothermicity of the reactions it supports.

JFM classification

Acoustics: Acoustics Instability: Instability Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 330 - 361
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berry, S. A., Auslender, A. H., Dilley, A. D. & Calleja, J. F. 2001 Hypersonic boundary-layer trip development for Hyper-X. J. Spacecr. Rockets 38 (6), 853–864.Google Scholar
Criminale, W. O., Jackson, T. L. & Joslin, R. D. 2003 Theory and Computation in Hydrodynamic Stability. Cambridge University Press.Google Scholar
Doraiswamy, S., Kelley, J. D. & Candler, G. V. 2010 Vibrational modelling of ${\mathrm{CO} }_{2} $ in high-enthalpy nozzle flows. J. Thermophys. Heat Transfer 24 (1), 9–17.Google Scholar
Fedorov, A. V. 2003 Receptivity of a high-speed boundary layer to acoustic disturbances. J. Fluid Mech. 491, 101–129.Google Scholar
Fedorov, A. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.CrossRefGoogle Scholar
Fedorov, A. & Tumin, A. 2003 Initial-value problem for hypersonic boundary-layer flows. AIAA J. 41 (3), 379–389.Google Scholar
Fox, R. O. 2003 Computational Models for Turbulent Reacting Flows. Cambridge University Press.CrossRefGoogle Scholar
Fridman, A. 2008 Plasma Chemistry. Cambridge University Press.Google Scholar
Fujii, K. & Hornung, H. G. 2003 Experimental investigation of high-enthalpy effects on attachment-line boundary-layer transition. AIAA J. 41 (7), 1282–1291.Google Scholar
Gaster, M., Kit, E. & Wygnanski, I. 1985 Large-scale structures in a forced turbulent mixing layer. J. Fluid Mech. 150, 23–40.Google Scholar
Grasso, F., Purpura, C., Chanetz, B. & Delery, J. 2003 Type III and type IV shock/shock interferences: theoretical and experimental aspects. Aerosp. Sci. Technol. 7 (2), 93–106.Google Scholar
Gudmundsson, K. 2010 Instability wave models of turbulent jets from round and serrated nozzles. PhD thesis, California Institute of Technology.Google Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.Google Scholar
Hardee, P. E. 2000 On three-dimensional structures in relativistic hydrodynamic jets. Astrophys. J. 533, 176.CrossRefGoogle Scholar
Holden, M. S. 1966 Experimental studies of separated flows at hypersonic speeds. Part 1. Separated flows over axisymmetric spiked bodies. AIAA J. 4, 591–599.Google Scholar
Horvath, T. J., Berry, S. A & Merski, N. R. 2004 Hypersonic boundary/shear layer transition for blunt to slender configurations: a NASA Langley experimental perspective. Tech. Rep. RTO-MP-AVT-111, NATO Research and Technology Organisation (RTO).Google Scholar
Jackson, T. L. & Grosch, C. E. 1990 Absolute/convective instabilities and the convective Mach number in a compressible mixing layer. Phys. Fluids A 2 (6), 949–954.Google Scholar
Johnson, H. B., Seipp, T. G. & Candler, G. V. 1998 Numerical study of hypersonic reacting boundary layer transition on cones. Phys. Fluids 10, 2676–2685.Google Scholar
Kee, R. J., Dixon-Lewis, G., Warnatz, J., Coltrin, M. E. & Miller, J. A. 1986 A FORTRAN computer code package for the evaluation of gas-phase multicomponent transport properties. Report SAND86-8246, Sandia National Laboratories.Google Scholar
Leyva, I. A. 2008 Transition delay in hypervelocity boundary layers by means of ${\mathrm{CO} }_{2} $ /acoustic instability interactions. Tech. Rep. AFRL-RZ-ED-TP-2008-578, Air Force Research Lab Edwards AFB (CA) Propulsion Directorate.Google Scholar
Leyva, I. A., Laurence, S., Beierholm, A. W., Hornung, H. G., Wagnild, R. M. & Candler, G. V. 2009 Transition delay in hypervelocity boundary layers by means of ${\mathrm{CO} }_{2} $ /acoustic instability interactions. AIAA paper 2009-1287.Google Scholar
Mack, L. M. 1990 On the inviscid acoustic-mode instability of supersonic shear flows. Theor. Comput. Fluid Dyn. 2 (2), 97–123.Google Scholar
Malik, M. R. & Chang, C. L. 2000 Nonparallel and nonlinear stability of supersonic jet flow. Comput. Fluids 29 (3), 327–365.Google Scholar
Massa, L. 2009 Spatial linear analysis of the flow in a solid rocket motor with burning walls. Combust. Flame 156 (4), 865–888.Google Scholar
Massa, L. 2012 Effect of carbon content on supersonic shear-layer instability. J. Fluid Mech. 693, 261–296.Google Scholar
Massa, L., Austin, J. M. & Jackson, T. L. 2007 Triple-point shear layers in gaseous detonation waves. J. Fluid Mech. 586, 205–248.Google Scholar
Morrison, G. L. & McLaughlin, D. K. 1980 Instability process in low Reynolds number supersonic jets. AIAA J. 18, 793–800.Google Scholar
Nichols, J. W. & Lele, S. K. 2011 Global modes and transient response of a cold supersonic jet. J. Fluid Mech. 669, 225–241.Google Scholar
Nicoud, F. & Poinsot, T. 2005 Thermoacoustic instabilities: Should the Rayleigh criterion be extended to include entropy changes? Combust. Flame 142 (1–2), 153–159.Google Scholar
Ortega, J. M. & Rheinboldt, W. C. 2000 Iterative Solution of Nonlinear Equations in Several Variables. SIAM.Google Scholar
Reda, D. C., Wilder, M. C. & Prabhu, D. K. 2010 Transition experiments on blunt bodies with isolated roughness elements in hypersonic flight. J. Spacecr. Rockets 47, 828–835.Google Scholar
Reynolds, W. C. & Hussain, A. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54, 263–288.Google Scholar
Rothman, L. S., Gordon, I. E., Barber, R. J., Dothe, H., Gamache, R. R., Goldman, A., Perevalov, V. I., Tashkun, S. A. & Tennyson, J. 2010 HITEMP, the high-temperature molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transfer 111 (15), 2139–2150.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schwartz, R. N., Slawsky, Z. I. & Herzfeld, K. F. 1591 Calculation of vibrational relaxation times in gases. J. Chem. Phys. 20.Google Scholar
Smits, A. J. & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer.Google Scholar
Suponitsky, V., Sandham, N. D. & Morfey, C. L. 2010 Linear and nonlinear mechanisms of sound radiation by instability waves in subsonic jets. J. Fluid Mech. 658, 509–538.Google Scholar
Tam, C. K. W. 1995 Supersonic jet noise. Annu. Rev. Fluid Mech. 27, 17–43.Google Scholar
Tam, C. K. W. & Hu, F. Q. 1989a The instability and acoustic wave modes of supersonic mixing layers inside a rectangular channel. J. Fluid Mech. 203, 51–76.Google Scholar
Tam, C. K. W. & Hu, F. Q. 1989b On the three families of instability waves of high-speed jets. J. Fluid Mech. 201, 447–483.Google Scholar
Vreman, A. W., Sandham, N. D. & Luo, K. H. 1996 Compressible mixing layer growth rate and turbulence characteristics. J. Fluid Mech. 320 (1), 235–258.Google Scholar