Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shim, Gihun
Park, Hyeongjun
Lee, Seulgi
and
Lee, Changhoon
2020.
Behavior of microbubbles in homogeneous stratified turbulence.
Physical Review Fluids,
Vol. 5,
Issue. 7,
Kim, Jin-Tae
Jin, Yaqing
Shen, Shikun
Dash, Ankan
and
Chamorro, Leonardo P.
2020.
Free fall of homogeneous and heterogeneous cones.
Physical Review Fluids,
Vol. 5,
Issue. 9,
Shim, Hyoeun
and
Lee, Changhoon
2021.
Two-way interaction between isotropic turbulence and dispersed bubbles.
Journal of Mechanical Science and Technology,
Vol. 35,
Issue. 4,
p.
1527.
Ni, Xiaoyue
Ouyang, Wei
Jeong, Hyoyoung
Kim, Jin-Tae
Tzavelis, Andreas
Mirzazadeh, Ali
Wu, Changsheng
Lee, Jong Yoon
Keller, Matthew
Mummidisetty, Chaithanya K.
Patel, Manish
Shawen, Nicholas
Huang, Joy
Chen, Hope
Ravi, Sowmya
Chang, Jan-Kai
Lee, KunHyuck
Wu, Yixin
Lie, Ferrona
Kang, Youn J.
Kim, Jong Uk
Chamorro, Leonardo P.
Banks, Anthony R.
Bharat, Ankit
Jayaraman, Arun
Xu, Shuai
and
Rogers, John A.
2021.
Automated, multiparametric monitoring of respiratory biomarkers and vital signs in clinical and home settings for COVID-19 patients.
Proceedings of the National Academy of Sciences,
Vol. 118,
Issue. 19,
Kim, Bong Hoon
Li, Kan
Kim, Jin-Tae
Park, Yoonseok
Jang, Hokyung
Wang, Xueju
Xie, Zhaoqian
Won, Sang Min
Yoon, Hong-Joon
Lee, Geumbee
Jang, Woo Jin
Lee, Kun Hyuck
Chung, Ted S.
Jung, Yei Hwan
Heo, Seung Yun
Lee, Yechan
Kim, Juyun
Cai, Tengfei
Kim, Yeonha
Prasopsukh, Poom
Yu, Yongjoon
Yu, Xinge
Avila, Raudel
Luan, Haiwen
Song, Honglie
Zhu, Feng
Zhao, Ying
Chen, Lin
Han, Seung Ho
Kim, Jiwoong
Oh, Soong Ju
Lee, Heon
Lee, Chi Hwan
Huang, Yonggang
Chamorro, Leonardo P.
Zhang, Yihui
and
Rogers, John A.
2021.
Three-dimensional electronic microfliers inspired by wind-dispersed seeds.
Nature,
Vol. 597,
Issue. 7877,
p.
503.
Chen, Dayi
Kim, Jin-Tae
Chamorro, Leonardo P.
and
Timperman, Aaron T.
2021.
Exceeding ohmic scaling by more than one order of magnitude with a 3D ion concentration polarization system.
Lab on a Chip,
Vol. 21,
Issue. 16,
p.
3094.
Kim, Jin-Tae
Kim, Yongsang
Kang, Soohyeon
Nam, Jaewook
Lee, Changhoon
and
Chamorro, Leonardo P.
2021.
Effect of the aspect ratio on the dynamics of air bubbles within Rayleigh–Bénard convection.
Physics of Fluids,
Vol. 33,
Issue. 9,
Liu, Claire
Kim, Jin‐Tae
Kwak, Sung Soo
Hourlier‐Fargette, Aurelie
Avila, Raudel
Vogl, Jamie
Tzavelis, Andreas
Chung, Ha Uk
Lee, Jong Yoon
Kim, Dong Hyun
Ryu, Dennis
Fields, Kelsey B.
Ciatti, Joanna L.
Li, Shupeng
Irie, Masahiro
Bradley, Allison
Shukla, Avani
Chavez, Jairo
Dunne, Emma C.
Kim, Seung Sik
Kim, Jungwoo
Park, Jun Bin
Jo, Han Heul
Kim, Joohee
Johnson, Michael C.
Kwak, Jean Won
Madhvapathy, Surabhi R.
Xu, Shuai
Rand, Casey M.
Marsillio, Lauren E.
Hong, Sue J.
Huang, Yonggang
Weese‐Mayer, Debra E.
and
Rogers, John A.
2021.
Wireless, Skin‐Interfaced Devices for Pediatric Critical Care: Application to Continuous, Noninvasive Blood Pressure Monitoring.
Advanced Healthcare Materials,
Vol. 10,
Issue. 17,
Jeong, Hyoyoung
Lee, Jong Yoon
Lee, KunHyuck
Kang, Youn J.
Kim, Jin-Tae
Avila, Raudel
Tzavelis, Andreas
Kim, Joohee
Ryu, Hanjun
Kwak, Sung Soo
Kim, Jong Uk
Banks, Aaron
Jang, Hokyung
Chang, Jan-Kai
Li, Shupeng
Mummidisetty, Chaithanya K.
Park, Yoonseok
Nappi, Simone
Chun, Keum San
Lee, Young Joong
Kwon, Kyeongha
Ni, Xiaoyue
Chung, Ha Uk
Luan, Haiwen
Kim, Jae-Hwan
Wu, Changsheng
Xu, Shuai
Banks, Anthony
Jayaraman, Arun
Huang, Yonggang
and
Rogers, John A.
2021.
Differential cardiopulmonary monitoring system for artifact-canceled physiological tracking of athletes, workers, and COVID-19 patients.
Science Advances,
Vol. 7,
Issue. 20,
Shim, Gihun
Kim, Jongsu
and
Lee, Changhoon
2021.
Path instability of a no-slip spheroidal bubble in isotropic turbulence.
Physical Review Fluids,
Vol. 6,
Issue. 7,
Wu, Yixin
Wu, Mingzheng
Vázquez-Guardado, Abraham
Kim, Joohee
Zhang, Xin
Avila, Raudel
Kim, Jin-Tae
Deng, Yujun
Yu, Yongjoon
Melzer, Sarah
Bai, Yun
Yoon, Hyoseo
Meng, Lingzi
Zhang, Yi
Guo, Hexia
Hong, Liu
Kanatzidis, Evangelos E.
Haney, Chad R.
Waters, Emily A.
Banks, Anthony R.
Hu, Ziying
Lie, Ferrona
Chamorro, Leonardo P.
Sabatini, Bernardo L.
Huang, Yonggang
Kozorovitskiy, Yevgenia
and
Rogers, John A.
2022.
Wireless multi-lateral optofluidic microsystems for real-time programmable optogenetics and photopharmacology.
Nature Communications,
Vol. 13,
Issue. 1,
Yang, Quansan
Hu, Ziying
Seo, Min-Ho
Xu, Yameng
Yan, Ying
Hsu, Yen-Hao
Berkovich, Jaime
Lee, Kwonjae
Liu, Tzu-Li
McDonald, Samantha
Nie, Haolin
Oh, Hannah
Wu, Mingzheng
Kim, Jin-Tae
Miller, Stephen A.
Jia, Ying
Butun, Serkan
Bai, Wubin
Guo, Hexia
Choi, Junhwan
Banks, Anthony
Ray, Wilson Z.
Kozorovitskiy, Yevgenia
Becker, Matthew L.
Pet, Mitchell A.
MacEwan, Matthew R.
Chang, Jan-Kai
Wang, Heling
Huang, Yonggang
and
Rogers, John A.
2022.
High-speed, scanned laser structuring of multi-layered eco/bioresorbable materials for advanced electronic systems.
Nature Communications,
Vol. 13,
Issue. 1,
Kim, Jin-Tae
Ouyang, Wei
Hwang, Hanul
Jeong, Hyoyoung
Kang, Soohyeon
Bose, Sanjeeb
Kwak, Sung Soo
Ni, Xiaoyue
Kim, Hyeonsu
Park, Jaehong
Chen, Hope
Soetikno, Alan
Kim, Joohee
Xu, Shuai
Chamorro, Leonardo P.
and
Rogers, John A.
2022.
Dynamics of plosive consonants via imaging, computations, and soft electronics.
Proceedings of the National Academy of Sciences,
Vol. 119,
Issue. 46,
Kang, Soohyeon
Cheng, Shyuan
Hong, Liu
Kim, Jin-Tae
and
Chamorro, Leonardo P.
2023.
Single sidewall cooling modulation on Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 957,
Issue. ,
Yang, Rui
Howland, Christopher J.
Liu, Hao-Ran
Verzicco, Roberto
and
Lohse, Detlef
2023.
Morphology evolution of a melting solid layer above its melt heated from below.
Journal of Fluid Mechanics,
Vol. 956,
Issue. ,
Kim, Jin-Tae
Yoon, Hong-Joon
Cheng, Shyuan
Liu, Fei
Kang, Soohyeon
Paudel, Shashwot
Cho, Donghwi
Luan, Haiwen
Lee, Minkyu
Jeong, Gooyoon
Park, Jaehong
Huang, Yu-Ting
Lee, Su Eon
Cho, Min
Lee, Geonhee
Han, Mengdi
Kim, Bong Hoon
Yan, Jinhui
Park, Yoonseok
Jung, Sunghwan
Chamorro, Leonardo P
Rogers, John A
and
Amon, Cristina
2024.
Functional bio-inspired hybrid fliers with separated ring and leading edge vortices.
PNAS Nexus,
Vol. 3,
Issue. 3,
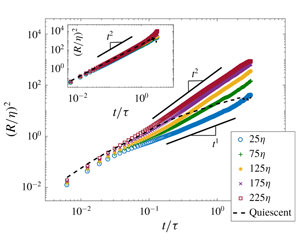
 $Ra=5.5\times 10^{9}$ and
$Ra=5.5\times 10^{9}$ and  $1.1\times 10^{10}$, where streams of 1 mm bubbles were released at various locations from the bottom of the tank along the path of the roll structure. Using three-dimensional particle tracking velocimetry, we simultaneously tracked a large number of bubbles to inspect the pair dispersion,
$1.1\times 10^{10}$, where streams of 1 mm bubbles were released at various locations from the bottom of the tank along the path of the roll structure. Using three-dimensional particle tracking velocimetry, we simultaneously tracked a large number of bubbles to inspect the pair dispersion,  $R^{2}(t)$, for a range of initial separations,
$R^{2}(t)$, for a range of initial separations,  $r$, spanning one order of magnitude, namely
$r$, spanning one order of magnitude, namely  $25\unicode[STIX]{x1D702}\leqslant r\leqslant 225\unicode[STIX]{x1D702}$; here
$25\unicode[STIX]{x1D702}\leqslant r\leqslant 225\unicode[STIX]{x1D702}$; here  $\unicode[STIX]{x1D702}$ is the local Kolmogorov length scale. Pair dispersion,
$\unicode[STIX]{x1D702}$ is the local Kolmogorov length scale. Pair dispersion,  $R^{2}(t)$, of the bubbles within a quiescent medium was also determined to assess the effect of inhomogeneity and anisotropy induced by the RB convection. Results show that
$R^{2}(t)$, of the bubbles within a quiescent medium was also determined to assess the effect of inhomogeneity and anisotropy induced by the RB convection. Results show that  $R^{2}(t)$ underwent a transition phase similar to the ballistic-to-diffusive (
$R^{2}(t)$ underwent a transition phase similar to the ballistic-to-diffusive ( $t^{2}$-to-
$t^{2}$-to- $t^{1}$) regime in the vicinity of the cell centre; it approached a bulk behavior
$t^{1}$) regime in the vicinity of the cell centre; it approached a bulk behavior  $t^{3/2}$ in the diffusive regime as the distance away from the cell centre increased. At small
$t^{3/2}$ in the diffusive regime as the distance away from the cell centre increased. At small  $r$,
$r$,  $R^{2}(t)\propto t^{1}$ is shown in the diffusive regime with a lower magnitude compared to the quiescent case, indicating that the convective turbulence reduced the amplitude of the bubble’s fluctuations. This phenomenon associated to the bubble path instability was further explored by the autocorrelation of the bubble’s horizontal velocity. At large initial separations,
$R^{2}(t)\propto t^{1}$ is shown in the diffusive regime with a lower magnitude compared to the quiescent case, indicating that the convective turbulence reduced the amplitude of the bubble’s fluctuations. This phenomenon associated to the bubble path instability was further explored by the autocorrelation of the bubble’s horizontal velocity. At large initial separations,  $R^{2}(t)\propto t^{2}$ was observed, showing the effect of the roll structure.
$R^{2}(t)\propto t^{2}$ was observed, showing the effect of the roll structure.