Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T08:51:10.908Z Has data issue: false hasContentIssue false
  • English
  • Français

On high-speed impingement of cylindrical droplets upon solid wall considering cavitation effects

Published online by Cambridge University Press:  30 October 2018

Wangxia Wu ,
Gaoming Xiang Open the ORCID record for Gaoming Xiang [Opens in a new window]  and
Bing Wang Open the ORCID record for Bing Wang [Opens in a new window]
Wangxia Wu
Affiliation:
School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
Gaoming Xiang
Affiliation:
School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
Bing Wang*
Affiliation:
School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The high-speed impingement of droplets on a wall occurs widely in nature and industry. However, there is limited research available on the physical mechanism of the complicated flow phenomena during impact. In this study, a simplified multi-component compressible two-phase fluid model, coupled with the phase-transition procedure, is employed to solve the two-phase hydrodynamics system for high-speed cylindrical droplet impaction on a solid wall. The threshold conditions of the thermodynamic parameters of the fluid are established to numerically model the initiation of phase transition. The inception of cavitation inside the high-speed cylindrical droplets impacting on the solid wall can thus be captured. The morphology and dynamic characteristics of the high-speed droplet impingement process are analysed qualitatively and quantitatively, after the mathematical models and numerical procedures are carefully verified and validated. It was found that a confined curved shock wave is generated when the high-speed cylindrical droplet impacts the wall and this shock wave is reflected by the curved droplet surface. A series of rarefaction waves focus at a position at a distance of one third of the droplet diameter away from the top pole due to the curved surface reflection. This focusing zone is identified as the cavity because the local liquid state satisfies the condition for the inception of cavitation. Moreover, the subsequent evolution of the cavitation zone is demonstrated and the effects of the impact speed, ranging from 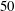$50$ to 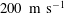$200~\text{m}~\text{s}^{-1}$, on the deformation of the cylindrical droplet and the further evolution of the cavitation were studied. The focusing position, where the cavitation core is located, is independent of the initial impaction speed. However, the cavity zone is enlarged and the stronger collapsing wave is induced as the impaction speed increases.

JFM classification

Drops and Bubbles: Cavitation Drops and Bubbles: Drops Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , pp. 851 - 877
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmad, M., Casey, M. & Sürken, N. 2009 Experimental assessment of droplet impact erosion resistance of steam turbine blade materials. Wear 267 (9), 1605–1618.Google Scholar
Ando, K., Colonius, T. & Brennen, C. E. 2011 Numerical simulation of shock propagation in a polydisperse bubbly liquid. Intl J. Multiphase Flow 37 (6), 596–608.Google Scholar
Azouzi, M. E. M., Ramboz, C., Lenain, J. F. & Caupin, F. 2013 A coherent picture of water at extreme negative pressure. Nat. Phys. 9 (1), 38–41.Google Scholar
Baer, M. R. & Nunziato, J. W. 1986 A two-phase mixture theory for the deflagration-to-detonation transition (ddt) in reactive granular materials. Intl J. Multiphase Flow 12 (6), 861–889.Google Scholar
Bowden, F. P. & Field, J. E. 1964 The brittle fracture of solids by liquid impact, by solid impact, and by shock. Proc. R. Soc. Lond. A 282 (1390), 331–352.Google Scholar
Brennen, C. E. 2013 Cavitation and Bubble Dynamics. Cambridge University Press.Google Scholar
Camus, J. J.1971 High speed flow in impact and its effect on solid surfaces. PhD thesis, University of Cambridge.Google Scholar
Caupin, F. & Herbert, E. 2006 Cavitation in water: a review. C. R. Phys. 7 (9–10), 1000–1017.Google Scholar
Cook, S. S. 1928 Erosion by water-hammer. Proc. R. Soc. Lond. A 119 (783), 481–488.Google Scholar
Coralic, V. & Colonius, T. 2014 Finite-volume WENO scheme for viscous compressible multicomponent flows. J. Comput. Phys. 274, 95–121.Google Scholar
Eggers, J., Fontelos, M. A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22 (6), 062101.Google Scholar
Field, J. E., Dear, J. P. & Ogren, J. E. 1989 The effects of target compliance on liquid drop impact. J. Appl. Phys. 65 (2), 533–540.Google Scholar
Field, J. E., Camus, J. J., Tinguely, M., Obreschkow, D. & Farhat, M. 2012 Cavitation in impacted drops and jets and the effect on erosion damage thresholds. Wear 290, 154–160.Google Scholar
Fisher, J. C. 1948 The fracture of liquids. J. Appl. Phys. 19 (11), 1062–1067.Google Scholar
Fuster, D. & Colonius, T. 2011 Modelling bubble clusters in compressible liquids. J. Fluid Mech. 688, 352–389.Google Scholar
Gottlieb, S. & Shu, C. W. 1998 Total variation diminishing Runge–Kutta schemes. Math. Comput. Amer. Math. Soc. 67 (221), 73–85.Google Scholar
Haller, K. K., Poulikakos, D., Ventikos, Y. & Monkewitz, P. 2003 Shock wave formation in droplet impact on a rigid surface: lateral liquid motion and multiple wave structure in the contact line region. J. Fluid Mech. 490, 1–14.Google Scholar
Haller, K. K., Ventikos, Y., Poulikakos, D. & Monkewitz, P. 2002 Computational study of high-speed liquid droplet impact. J. Appl. Phys. 92 (5), 2821–2828.Google Scholar
Han, E., Hantke, M. & Müller, S. 2017 Efficient and robust relaxation procedures for multi-component mixtures including phase transition. J. Comput. Phys 338, 217–239.Google Scholar
Han, Y., Xie, Y. & Zhang, D. 2012 Numerical study on high-speed impact between a water droplet and a deformable solid surface. In ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, pp. 675–683. American Society of Mechanical Engineers.Google Scholar
Hansson, I. & Mørch, K. A. 1980 The dynamics of cavity clusters in ultrasonic (vibratory) cavitation erosion. J. Appl. Phys. 51 (9), 4651–4658.Google Scholar
Herbert, E. & Caupin, F. 2005 The limit of metastability of water under tension: theories and experiments. J. Phys.: Condens. Matter 17 (45), S3597.Google Scholar
Heymann, F. J. 1969 High-speed impact between a liquid drop and a solid surface. J. Appl. Phys. 40 (13), 5113–5122.Google Scholar
Johnsen, E. & Colonius, T. 2006 Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 219 (2), 715–732.Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.Google Scholar
Kondo, T. & Ando, K. 2016 One-way-coupling simulation of cavitation accompanied by high-speed droplet impact. Phys. Fluids 28 (3), 033303.Google Scholar
Lesser, M. B. 1981 Analytic solutions of liquid-drop impact problems. Proc. R. Soc. Lond. A 377 (1770), 289–308.Google Scholar
Momber, A. W. 2006 A transition index for rock failure due to liquid impact. Wear 260 (9), 996–1002.Google Scholar
Momber, A. W. 2016 The response of geo-materials to high-speed liquid drop impact. Intl J. Impact Engng 89, 83–101.Google Scholar
Müller, I. & Müller, W. H. 2009 Fundamentals of Thermodynamics and Applications. Springer.Google Scholar
Mundo, C. H. R., Sommerfeld, M. & Tropea, C. 1995 Droplet-wall collisions: experimental studies of the deformation and breakup process. Intl J. Multiphase Flow 21 (2), 151–173.Google Scholar
Niu, Y. Y. & Wang, H. W. 2016 Simulations of the shock waves and cavitation bubbles during a three-dimensional high-speed droplet impingement based on a two-fluid model. Comput. Fluids 134, 196–214.Google Scholar
Obreschkow, D., Dorsaz, N., Kobel, P., de Bosset, A., Tinguely, M., Field, J. & Farhat, M. 2011 Confined shocks inside isolated liquid volumes: a new path of erosion? Phys. Fluids 23 (10), 101702.Google Scholar
Oka, Y. I., Mihara, S. & Miyata, H. 2007 Effective parameters for erosion caused by water droplet impingement and applications to surface treatment technology. Wear 263 (1), 386–394.Google Scholar
Oka, Y. I. & Miyata, H. 2009 Erosion behaviour of ceramic bulk and coating materials caused by water droplet impingement. Wear 267 (11), 1804–1810.Google Scholar
Okada, H., Uchida, S., Naitoh, M., Xiong, J. & Koshizuka, S. 2011 Evaluation methods for corrosion damage of components in cooling systems of nuclear power plants by coupling analysis of corrosion and flow dynamics (v) flow-accelerated corrosion under single- and two-phase flow conditions. J. Nucl. Sci. Technol. 48 (1), 65–75.Google Scholar
Pasandideh-Fard, M., Qiao, Y. M., Chandra, S. & Mostaghimi, J. 1996 Capillary effects during droplet impact on a solid surface. Phys. Fluids 8 (3), 650–659.Google Scholar
Pelanti, M. & Shyue, K. M. 2014 A mixture-energy-consistent six-equation two-phase numerical model for fluids with interfaces, cavitation and evaporation waves. J. Comput. Phys. 259, 331–357.Google Scholar
Petitpas, F., Franquet, E., Saurel, R. & Le Metayer, O. 2007 A relaxation-projection method for compressible flows. Part II. Artificial heat exchanges for multiphase shocks. J. Comput. Phys. 225 (2), 2214–2248.Google Scholar
Rein, M. 1993 Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 12 (2), 61–93.Google Scholar
Sanada, T., Ando, K. & Colonius, T. 2011 A computational study of high-speed droplet impact. Fluid Dyn. Mater. Process. 7 (4), 329–340.Google Scholar
Sanada, T., Watanabe, M., Shirota, M., Yamase, M. & Saito, T. 2008 Impact of high-speed steam-droplet spray on solid surface. Fluid Dyn. Res. 40 (7), 627–636.Google Scholar
Saurel, R. & Abgrall, R. 1999 A multiphase Godunov method for compressible multifluid and multiphase flows. J. Comput. Phys. 150 (2), 425–467.Google Scholar
Saurel, R., Boivin, P. & Le Métayer, O. 2016 A general formulation for cavitating, boiling and evaporating flows. Comput. Fluids 128, 53–64.Google Scholar
Saurel, R. & Petitpas, F. 2013 Introduction to diffuse interfaces and transformation fronts modelling in compressible media. In ESAIM: Proceedings, pp. 124–143. EDP Sciences.Google Scholar
Saurel, R., Petitpas, F. & Abgrall, R. 2008 Modelling phase transition in metastable liquids: application to cavitating and flashing flows. J. Fluid Mech. 607, 313–350.Google Scholar
Sembian, S., Liverts, M., Tillmark, N. & Apazidis, N. 2016 Plane shock wave interaction with a cylindrical water column. Phys. Fluids 28 (5), 056102.Google Scholar
Soto, D., De Lariviere, A. B., Boutillon, X., Clanet, C. & Quéré, D. 2014 The force of impacting rain. Soft Matt. 10 (27), 4929–4934.Google Scholar
Thompson, K. W. 1987 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 68 (1), 1–24.Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K., Ootsuka, N. & Hatsuki, Y. 2005 The air bubble entrapped under a drop impacting on a solid surface. J. Fluid Mech. 545 (-1), 203–212.Google Scholar
Thoroddsen, S. T., Takehara, K. & Etoh, T. G. 2010 Bubble entrapment through topological change. Phys. Fluids 22 (5), 051701.Google Scholar
Thoroddsen, S. T., Takehara, K. & Etoh, T. G. 2012 Micro-splashing by drop impacts. J. Fluid Mech. 706, 560–570.Google Scholar
Titarev, V. A. & Toro, E. F. 2004 Finite-volume WENO schemes for three-dimensional conservation laws. J. Comput. Phys. 201 (1), 238–260.Google Scholar
Toro, E. F. 2013 Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer Science & Business Media.Google Scholar
Trevena, D. H. 1984 Cavitation and the generation of tension in liquids. J. Phys. D 17 (11), 2139.Google Scholar
Xiang, G. & Wang, B. 2017 Numerical study of a planar shock interacting with a cylindrical water column embedded with an air cavity. J. Fluid Mech. 825, 825–852.Google Scholar
Xiong, J., Koshizuka, S. & Sakai, M. 2010 Numerical analysis of droplet impingement using the moving particle semi-implicit method. J. Nucl. Sci. Technol. 47 (3), 314–321.Google Scholar
Xiong, J., Koshizuka, S. & Sakai, M. 2011 Investigation of droplet impingement onto wet walls based on simulation using particle method. J. Nucl. Sci. Technol. 48 (1), 145–153.Google Scholar
Xiong, J., Koshizuka, S., Sakai, M. & Ohshima, H. 2012 Investigation on droplet impingement erosion during steam generator tube failure accident. Nucl. Engng Des. 249, 132–139.Google Scholar
Yarin, A. L. 2005 Drop impact dynamics: splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 38 (1), 159–192.Google Scholar
Zein, A., Hantke, M. & Warnecke, G. 2010 Modeling phase transition for compressible two-phase flows applied to metastable liquids. J. Comput. Phys. 229 (8), 2964–2998.Google Scholar
Zein, A., Hantke, M. & Warnecke, G. 2013 On the modeling and simulation of a laser-induced cavitation bubble. Intl J. Numer. Meth. Fluids 73 (2), 172–203.Google Scholar