Published online by Cambridge University Press: 07 February 2019
The drag reduction characteristics and sustainability bounds of superhydrophobic (SH) surfaces in high Reynolds number turbulent flows are investigated using results from direct numerical simulation (DNS) and scaling-law analysis. The DNS studies were performed, using lattice Boltzmann methods, in turbulent channel flows at bulk Reynolds numbers of 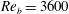 $Re_{b}=3600$ (
$Re_{b}=3600$ (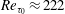 $Re_{\unicode[STIX]{x1D70F}_{0}}\approx 222$) and
$Re_{\unicode[STIX]{x1D70F}_{0}}\approx 222$) and 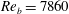 $Re_{b}=7860$ (
$Re_{b}=7860$ (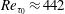 $Re_{\unicode[STIX]{x1D70F}_{0}}\approx 442$) with SH longitudinal microgrooves or SH aligned microposts on the walls. Surface microtexture geometrical parameters corresponding to microgroove widths or micropost spacings of
$Re_{\unicode[STIX]{x1D70F}_{0}}\approx 442$) with SH longitudinal microgrooves or SH aligned microposts on the walls. Surface microtexture geometrical parameters corresponding to microgroove widths or micropost spacings of 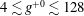 $4\lesssim g^{+0}\lesssim 128$ in base flow wall units and solid fractions of
$4\lesssim g^{+0}\lesssim 128$ in base flow wall units and solid fractions of 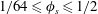 $1/64\leqslant \unicode[STIX]{x1D719}_{s}\leqslant 1/2$ were investigated at interface protrusion angles of
$1/64\leqslant \unicode[STIX]{x1D719}_{s}\leqslant 1/2$ were investigated at interface protrusion angles of 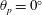 $\unicode[STIX]{x1D703}_{p}=0^{\circ }$ and
$\unicode[STIX]{x1D703}_{p}=0^{\circ }$ and 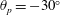 $\unicode[STIX]{x1D703}_{p}=-30^{\circ }$. Analysis of the governing equations and DNS results shows that the magnitude of drag reduction is not only a function of the geometry and size of the surface microtexture in wall units, but also the Reynolds number of the base flow. A Reynolds number independent measure of drag reduction can be constructed by parameterizing the magnitude of drag reduction in terms of the friction coefficient of the base flow and the shift,
$\unicode[STIX]{x1D703}_{p}=-30^{\circ }$. Analysis of the governing equations and DNS results shows that the magnitude of drag reduction is not only a function of the geometry and size of the surface microtexture in wall units, but also the Reynolds number of the base flow. A Reynolds number independent measure of drag reduction can be constructed by parameterizing the magnitude of drag reduction in terms of the friction coefficient of the base flow and the shift, 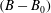 $(B-B_{0})$, in the intercept of a logarithmic law representation of the mean velocity profile in the flow with SH walls compared to the base flow, where
$(B-B_{0})$, in the intercept of a logarithmic law representation of the mean velocity profile in the flow with SH walls compared to the base flow, where 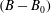 $(B-B_{0})$ is Reynolds number independent. The scaling laws for
$(B-B_{0})$ is Reynolds number independent. The scaling laws for 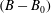 $(B-B_{0})$, in terms of the geometrical parameters of the surface microtexture in wall units, are presented for SH longitudinal microgrooves and aligned microposts. The same scaling laws are found to also apply to liquid-infused (LI) surfaces as long as the viscosity ratios are large,
$(B-B_{0})$, in terms of the geometrical parameters of the surface microtexture in wall units, are presented for SH longitudinal microgrooves and aligned microposts. The same scaling laws are found to also apply to liquid-infused (LI) surfaces as long as the viscosity ratios are large, 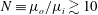 $N\equiv \unicode[STIX]{x1D707}_{o}/\unicode[STIX]{x1D707}_{i}\gtrsim 10$. These scaling laws, in conjunction with the parametrization of drag reduction in terms of
$N\equiv \unicode[STIX]{x1D707}_{o}/\unicode[STIX]{x1D707}_{i}\gtrsim 10$. These scaling laws, in conjunction with the parametrization of drag reduction in terms of 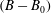 $(B-B_{0})$, allow for a priori prediction of the magnitude of drag reduction with SH or LI surfaces in turbulent flow at any Reynolds number. For the most stable of these SH surface microtextures, namely, longitudinal microgrooves, the pressure stability bounds of the SH surface under the pressure loads of turbulent flow are investigated. It is shown that the pressure stability bounds of SH surfaces are also significantly curtailed with increasing Reynolds number of the flow. Using these scaling laws, the narrow range of SH surface geometrical parameters which can yield large drag reduction as well as sustainability in high Reynolds number turbulent flows is identified.
$(B-B_{0})$, allow for a priori prediction of the magnitude of drag reduction with SH or LI surfaces in turbulent flow at any Reynolds number. For the most stable of these SH surface microtextures, namely, longitudinal microgrooves, the pressure stability bounds of the SH surface under the pressure loads of turbulent flow are investigated. It is shown that the pressure stability bounds of SH surfaces are also significantly curtailed with increasing Reynolds number of the flow. Using these scaling laws, the narrow range of SH surface geometrical parameters which can yield large drag reduction as well as sustainability in high Reynolds number turbulent flows is identified.