Article contents
Off-plane motion of a prolate capsule in shear flow
Published online by Cambridge University Press: 13 March 2013
Abstract
The objective of this study is to investigate the motion of an ellipsoidal capsule in a simple shear flow when its revolution axis is initially placed off the shear plane. We consider prolate capsules with an aspect ratio of two or three enclosed by a membrane, which is either strain-hardening or strain-softening. We seek the equilibrium motion of the capsule as we increase the capillary number 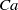 $\mathit{Ca}$, which measures the ratio between the viscous and elastic forces. The three-dimensional fluid–structure interaction problem is solved numerically by coupling a boundary integral method (for the internal and external flows) with a finite element method (for the wall deformation). For any initial inclination with the flow vorticity axis, a given capsule converges towards a unique equilibrium configuration which depends on
$\mathit{Ca}$, which measures the ratio between the viscous and elastic forces. The three-dimensional fluid–structure interaction problem is solved numerically by coupling a boundary integral method (for the internal and external flows) with a finite element method (for the wall deformation). For any initial inclination with the flow vorticity axis, a given capsule converges towards a unique equilibrium configuration which depends on 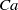 $\mathit{Ca}$. At low capillary number, the stable equilibrium motion is the rolling regime: the capsule aligns its long axis with the vorticity axis, while the membrane tank-treads. As
$\mathit{Ca}$. At low capillary number, the stable equilibrium motion is the rolling regime: the capsule aligns its long axis with the vorticity axis, while the membrane tank-treads. As 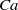 $\mathit{Ca}$ increases, the capsule takes a complex wobbling motion at equilibrium, precessing around the vorticity axis. As
$\mathit{Ca}$ increases, the capsule takes a complex wobbling motion at equilibrium, precessing around the vorticity axis. As 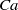 $\mathit{Ca}$ is further increased, the capsule long axis oscillates about the shear plane, while the membrane rotates around a capsule cross-section that also oscillates over time (oscillating–swinging regime). The amplitude of the oscillations about the shear plane decreases as
$\mathit{Ca}$ is further increased, the capsule long axis oscillates about the shear plane, while the membrane rotates around a capsule cross-section that also oscillates over time (oscillating–swinging regime). The amplitude of the oscillations about the shear plane decreases as 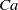 $\mathit{Ca}$ increases and the capsule finally takes a swinging motion in the shear plane. It is found that the transitions from rolling to wobbling and from wobbling to oscillating–swinging depend on the mean energy stored in the membrane.
$\mathit{Ca}$ increases and the capsule finally takes a swinging motion in the shear plane. It is found that the transitions from rolling to wobbling and from wobbling to oscillating–swinging depend on the mean energy stored in the membrane.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
Dupont et al. supplementary movie
Rolling motion of a prolate capsule with an aspect ratio of 2 and a strain-hardening Skalak membrane (C2SK). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 85°; the capillary number is Ca = 0.1. The points M and N are the membrane points initially located on the short and long axis respectively. Point P is at the tip of the long axis at time t.
Dupont et al. supplementary movie
Wobbling motion of a prolate capsule with an aspect ratio of 2 and a strain-hardening Skalak membrane (C2SK). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 15°; the capillary number is Ca = 0.9. The points M and N are the membrane points initially located on the short and long axis respectively. Point P is at the tip of the long axis at time t.
Dupont et al. supplementary movie
Oscillating-swinging of a prolate capsule with an aspect ratio of 2 and a strain-hardening Skalak membrane (C2SK). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 60°; the capillary number is Ca = 1.5. The points M and N are the membrane points initially located on the short and long axis respectively. Point P is at the tip of the long axis at time t.
- 42
- Cited by


