Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T08:33:14.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of viscous starting flow past wedges

Published online by Cambridge University Press:  19 July 2016

Ling Xu
Ling Xu*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents a numerical study of vortex formation in the impulsively started viscous flow past an infinite wedge, for wedge angles ranging from 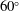$60^{\circ }$ to 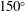$150^{\circ }$. The Navier–Stokes equations are solved in the vorticity-streamfunction formulation using a time-splitting scheme. The vorticity convection is computed using a semi-Lagrangian method. The vorticity diffusion is computed using an implicit finite difference scheme, after mapping the physical domain conformally onto a rectangle. The results show details of the vorticity evolution and associated streamline and streakline patterns. In particular, a hierarchical formation of recirculating regions corresponding to alternating signs of vorticity is revealed. The appearance times of these vorticity regions of alternate signs, as well as their dependence on the wedge angles, are investigated. The scaling behaviour of the vortex centre trajectory and vorticity is reported, and solutions are compared with those available from laboratory experiments and the inviscid similarity theory.

JFM classification

Boundary Layers: Boundary layer separation Geophysical and Geological Flows: Coastal engineering Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 150 - 165
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. D. Jr. 2005 Ludwig Prandtl’s boundary layer. Phys. Today (December) 58 (12), 42–48.CrossRefGoogle Scholar
Davies, P. A., Dakin, J. M. & Falconer, R. A. 1995 Eddy formation behind a coastal headland. J. Coast. Res. 11, 154–167.Google Scholar
Falcone, M. & Ferretti, R. 1998 Convergence analysis for a class of high-order semi-Lagrangian advection schemes. SIAM J. Numer. Anal. 33, 909–940.Google Scholar
Hudson, J. D. & Dennis, S. C. R. 1985 The flow of a viscous incompressible fluid past a normal flat plate at low and intermediate Reynolds numbers: the wake. J. Fluid Mech. 160, 369–383.Google Scholar
Jespersen, T. S., Thomassen, J. Q., Andersen, A. & Bohr, T. 2004 Vortex dynamics around a solid ripple in an oscillatory flow. Eur. Phys. J. B 38, 127–138.Google Scholar
Koumoutsakos, P. & Shiels, D. 1996 Simulation of the viscous flow normal to an impulsively started and uniformly accelerated flat plate. J. Fluid Mech. 328, 177–227.Google Scholar
Luchini, P. & Tognaccini, R. 2002 The start-up vortex issuing from a semi-infinite flat plate. J. Fluid Mech. 455, 175–193.Google Scholar
Pierce, D. 1961 Photographic evidence of the formation and growth of vorticity behind plates accelerated from rest in still air. J. Fluid Mech. 11, 460–464.Google Scholar
Pullin, D. I. 1978 The large-scale structure of unsteady self-similar rolled-up vortex sheets. J. Fluid Mech. 88, 401–430.Google Scholar
Pullin, D. I. & Perry, A. E. 1980 Some flow visualization experiments on the starting vortex. J. Fluid Mech. 97, 239–255.CrossRefGoogle Scholar
Strang, G. 1968 On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 5 (3), 506–517.Google Scholar
Xu, L. & Nitsche, M. 2014 Scaling behaviour in impulsively started viscous flow past a finite flat plate. J. Fluid Mech. 756, 689–715.CrossRefGoogle Scholar
Xu, L. & Nitsche, M. 2015 Start-up vortex flow past an accelerated flat plate. Phys. Fluids 27, 033602.Google Scholar