Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T08:28:47.077Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical study of the unstratified and stratified Ekman layer

Published online by Cambridge University Press:  26 August 2014

Enrico Deusebio ,
G. Brethouwer ,
P. Schlatter  and
E. Lindborg
Enrico Deusebio*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Cambridge CB3 0WA, UK Linné Flow Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
G. Brethouwer
Affiliation:
Linné Flow Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
P. Schlatter
Affiliation:
Linné Flow Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
E. Lindborg
Affiliation:
Linné Flow Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

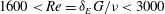We study the turbulent Ekman layer at moderately high Reynolds number, $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1600 < \mathit{Re} = \delta _{E}G/\nu < 3000$, using direct numerical simulations (DNS). Here, 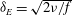$\delta _{E} = \sqrt{2\nu /f}$ is the laminar Ekman layer thickness, 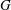$G$ the geostrophic wind, $\nu $ the kinematic viscosity and 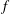$f$ is the Coriolis parameter. We present results for both neutrally, moderately and strongly stably stratified conditions. For unstratified cases, large-scale roll-like structures extending from the outer region down to the wall are observed. These structures have a clear dominant frequency and could be related to periodic oscillations or instabilities developing near the low-level jet. We discuss the effect of stratification and 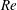$\mathit{Re}$ on one-point and two-point statistics. In the strongly stratified Ekman layer we observe stable co-existing large-scale laminar and turbulent patches appearing in the form of inclined bands, similar to other wall-bounded flows. For weaker stratification, continuously sustained turbulence strongly affected by buoyancy is produced. We discuss the scaling of turbulent length scales, height of the Ekman layer, friction velocity, veering angle at the wall and heat flux. The boundary-layer thickness, the friction velocity and the veering angle depend on 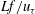$Lf/u_\tau $, where 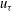$u_\tau $ is the friction velocity and 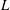$L$ the Obukhov length scale, whereas the heat fluxes appear to scale with 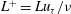$L^+=L u_\tau /\nu $.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 672 - 704
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1–42.Google Scholar
Barkley, D. & Tuckerman, L. S. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94 (1), 014502.CrossRefGoogle ScholarPubMed
Brethouwer, G., Duguet, Y. & Schlatter, P. 2012 Turbulent–laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 704, 137–172.Google Scholar
Brown, R. A. 1970 A secondary flow model for the planetary boundary layer. J. Atmos. Sci. 27 (5), 742–757.Google Scholar
Businger, J., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28 (2), 181–189.Google Scholar
Caldwell, D. R. & van Atta, C. W. 1970 Characteristics of Ekman boundary layer instabilities. J. Fluid Mech. 44 (1), 79–95.Google Scholar
Caldwell, D. R., Van Atta, C. W. & Helland, K. N. 1972 A laboratory study of the turbulent Ekman layer. Geophys. Astrophys. Fluid Dyn. 3 (1), 125–160.Google Scholar
Caughey, S. J. 1982 Observed characteristics of the atmospheric boundary layer. In Atmospheric Turbulence and Air Pollution Modelling, pp. 107–158. Springer.Google Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S.2007 simson – a pseudo-spectral solver for incompressible boundary layer flows. Tech Rep. KTH Mechanics, Stockholm, Sweden, TRITA-MEK 2007:07.Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696 (410), 434–467.CrossRefGoogle Scholar
Coleman, G. N. & Ferziger, J. H. 1996 Direct numerical simulation of a vigorously heated low Reynolds number convective boundary layer. Dyn. Atmos. Oceans 24 (1), 85–94.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1990 A numerical study of the turbulent Ekman layer. J. Fluid Mech. 213, 313–348.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1992 Direct simulation of the stably stratified turbulent Ekman layer. J. Fluid Mech. 244 (1), 677–712.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1994 A numerical study of the convective boundary layer. Boundary-Layer Meteorol. 70 (3), 247–272.CrossRefGoogle Scholar
Csanady, G. T. 1967 On the ‘resistance law’ of a turbulent Ekman layer. J. Atmos. Sci. 24, 467–471.Google Scholar
Deardorff, J. W. 1970 A three-dimensional numerical investigation of the idealized planetary boundary layer. Geophys. Astrophys. Fluid Dyn. 1 (3–4), 377–410.Google Scholar
Deusebio, E.2010 An open channel version of simson. Tech Rep. KTH Mechanics, Stockholm, Sweden.Google Scholar
Deusebio, E., Schlatter, P., Brethouwer, G. & Lindborg, E. 2011 Direct numerical simulations of stratified open channel flows. J. Phys.: Conf. Ser. 318 (2), 022009.Google Scholar
Dubos, T., Barthlott, C. & Drobinski, P. 2008 Emergence and secondary instability of Ekman layer rolls. J. Atmos. Sci. 65 (7), 2326–2342.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110 (3), 034502.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.Google Scholar
Ekman, V. W. 1905 On the influence of the Earth’s rotation on ocean currents. Arch. Math. Astron. Phys. 2, 1–52.Google Scholar
El Khoury, G., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91, 1–21.Google Scholar
Esau, I. N. 2003 The coriolis effect on coherent structures in planetary boundary layers. J. Turbul. 4 (1), 17.Google Scholar
Etling, D. & Brown, R. A. 1993 Roll vortices in the planetary boundary layer: a review. Boundary-Layer Meteorol. 65 (3), 215–248.Google Scholar
Etling, D. & Wippermann, F. 1975 On the instability of a planetary boundary layer with Rossby-number similarity. Boundary-Layer Meteorol. 9 (3), 341–360.Google Scholar
Faller, A. J. 1963 An experimental study of the instability of the laminar Ekman boundary layer. J. Fluid Mech. 15 (163), 560–576.Google Scholar
Faller, A. J. & Kaylor, R. E. 1966 A numerical study of the instability of the laminar Ekman boundary layer. J. Atmos. Sci. 23, 466–480.Google Scholar
Flores, O. & Riley, J. J. 2010 Analysis of turbulence collapse in stably stratified surface layers using direct numerical simulation. Boundary-Layer Meteorol. 129 (2), 241–259.Google Scholar
García-Villalba, M. & del Álamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23 (4), 045104.Google Scholar
Greenspan, H. P. 1990 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hamilton, J. H., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Handler, R. A., Saylor, J. R., Leighton, R. I. & Rovelstad, A. L. 1999 Transport of a passive scalar at a shear-free boundary in fully developed turbulent open channel flow. Phys. Fluids 11 (9), 2607–2625.Google Scholar
Högström, U. 1988 Non-dimensional wind and temperature profiles in the atmospheric surface layer: a re-evaluation. Boundary-Layer Meteorol. 42 (1–2), 55–78.Google Scholar
Holtslag, A. A. M. & Nieuwstadt, F. T. M. 1986 Scaling the atmospheric boundary layer. Boundary-Layer Meteorol. 36 (1–2), 201–209.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10 (4), 509–512.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $\mathit{Re}_\tau = 2003$ . Phys. Fluids 18 (1), 011702.Google Scholar
Jiménez, J.1998 The largest scales of turbulence. In Annual Research Briefs. Centre for Turbulence Research, Standford.Google Scholar
Kaimal, J. C., Wyngaard, J. C., Haugen, D. A., Coté, O. R., Izumi, Y., Caughey, S. J. & Readings, C. J. 1976 Turbulence structure in the convective boundary layer. J. Atmos. Sci. 33 (11), 2152–2169.Google Scholar
Komori, S., Ueda, H., Ogino, F. & Mizushina, T. 1983 Turbulence structure in stably stratified open-channel flow. J. Fluid Mech. 130, 13–26.Google Scholar
Kondo, J., Kanechika, O. & Yasuda, N. 1978 Heat and momentum transfers under strong stability in the atmospheric surface layer. J. Atmos. Sci. 35 (6), 1012–1021.Google Scholar
Lemone, M. A. 1973 The structure and dynamics of horizontal roll vortices in the planetary boundary layer. J. Atmos. Sci. 30 (6), 1077–1091.2.0.CO;2>CrossRefGoogle Scholar
Lilly, D. K. 1966 On the instability of Ekman boundary flow. J. Atmos. Sci. 23 (5), 481–494.Google Scholar
Mahrt, L. 1998 Nocturnal boundary-layer regimes. Boundary-Layer Meteorol. 88 (2), 255–278.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Mason, P. J. & Derbyshire, S. H. 1990 Large-eddy simulation of the stably-stratified atmospheric boundary layer. Boundary-Layer Meteorol. 53 (1–2), 117–162.CrossRefGoogle Scholar
Mason, P. J. & Thomson, D. J. 1987 Large-eddy simulations of the neutral-static-stability planetary boundary layer. Q. J. R. Astron. Soc. 113 (476), 413–443.Google Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011 The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.CrossRefGoogle Scholar
McNaughton, K. G. & Brunet, Y. 2002 Townsend’s hypothesis, coherent structures and Monin–Obukhov similarity. Boundary-Layer Meteorol. 102 (2), 161–175.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13, 692–701.CrossRefGoogle Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.Google Scholar
Miyashita, K., Iwamoto, K. & Kawamura, H. 2006 Direct numerical simulation of the neutrally stratified turbulent Ekman boundary layer. J. Earth Simulator 6, 3–15.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 151, 163–187.Google Scholar
Monin, A. A. S., Yaglom, A. M. & Lumley, J. L. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2. MIT Press.Google Scholar
Morris, K., Handler, R. A. & Rouson, D. 2011 Intermittency in the turbulent Ekman layer. J. Turbul. 12 (12).Google Scholar
Nieuwstadt, F. T. M. 1984 The turbulent structure of the stable, nocturnal boundary layer. J. Atmos. Sci. 41 (14), 2202–2216.Google Scholar
Nieuwstadt, F. T. M. 2005 Direct numerical simulation of stable channel flow at large stability. Boundary-Layer Meteorol. 116, 277–299.Google Scholar
Obukhov, A. M. 1946 Turbulence in thermally inhomogeneous atmosphere. Trudy Inst. Teor. Geofiz. Akad. Nauk SSSR 1, 95–115.Google Scholar
Örlü, R. & Schlatter, P. 2011 On the fluctuating wall-shear stress in zero pressure-gradient turbulent boundary layer flows. Phys. Fluids 23 (2), 021704.CrossRefGoogle Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.Google Scholar
Prigent, A., Grégoire, G., Chaté, H., Dauchot, O. & van Saarloos, W. 2002 Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 89 (1), 014501.Google Scholar
Schlatter, P., Li, Q., Brethouwer, G., Johansson, A. V. & Henningson, D. S. 2010 Simulations of spatially evolving turbulent boundary layers up to. Intl J. Heat Fluid Flow 31 (3), 251–261.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659 (1), 116–126.Google Scholar
Shingai, K. & Kawamura, H. 2002 Direct numerical simulation of turbulent heat transfer in the stably stratified Ekman layer. Therm. Sci. Engng 10, 25–33.Google Scholar
Shingai, K. & Kawamura, H. 2004 A study of turbulence structure and large-scale motion in the Ekman layer through direct numerical simulations. J. Turbul. 5 (13), 1–18.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Sous, D., Sommeria, J. & Boyer, D. 2013 Friction law and turbulent properties in a laboratory Ekman boundary layer. Phys. Fluids 25, 046602.CrossRefGoogle Scholar
Spalart, P. R. 1989 Theoretical and numerical study of a three-dimensional turbulent boundary layer. J. Fluid Mech. 205, 319–340.Google Scholar
Spalart, P. R., Coleman, G. N. & Johnstone, R. 2008 Direct numerical simulation of the Ekman layer: a step in Reynolds number, and cautious support for a log law with a shifted origin. Phys. Fluids 20, 101507.Google Scholar
Spalart, P. R., Coleman, G. N. & Johnstone, R. 2009 Retraction: Direct numerical simulation of the Ekman layer: a step in Reynolds number, and cautious support for a log law with a shifted origin. Phys. Fluids 21 (10), 109901.Google Scholar
Taylor, J. R. & Sarkar, S. 2007 Internal gravity waves generated by a turbulent bottom Ekman layer. J. Fluid Mech. 590, 331–354.Google Scholar
Taylor, J. R. & Sarkar, S. 2008a Direct and large eddy simulations of a bottom Ekman layer under an external stratification. Intl J. Heat Fluid Flow 29 (3), 721–732.Google Scholar
Taylor, J. R. & Sarkar, S. 2008b Stratification effects in a bottom Ekman layer. J. Phys. Oceanogr. 38 (11), 2535–2555.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation. Cambridge University Press, electronic version.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar
Wyngaard, J. C. 1973 On surface-layer turbulence. In Workshop in Micrometeorology, Boston, MA, pp. 101–149.Google Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.Google Scholar
Zilitinkevich, S. S. 1972 On the determination of the height of the Ekman boundary layer. Boundary-Layer Meteorol. 3 (2), 141–145.Google Scholar
Zilitinkevich, S. S. & Baklanov, A. 2002 Calculation of the height of the stable boundary layer in practical applications. Boundary-Layer Meteorol. 105 (3), 389–409.Google Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Rogachevskii, I., Esau, I., Mauritsen, T. & Miles, M. W. 2008 Turbulence energetics in stably stratified geophysical flows: strong and weak mixing regimes. Q. J. R. Meteorol. Soc. 134 (633), 793–799.Google Scholar
Zilitinkevich, S. S. & Esau, I. 2007 Similarity theory and calculation of turbulent fluxes at the surface for the stably stratified atmospheric boundary layer. Boundary-Layer Meteorol. 125 (2), 193–205.Google Scholar