Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T01:32:26.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical solution of unsteady boundary-layer separation in supersonic flow: upstream moving wall

Published online by Cambridge University Press:  03 July 2012

R. Yapalparvi  and
L. L. Van Dommelen
R. Yapalparvi*
Affiliation:
Department of Mathematics, McMaster University, 1280 Main St W, Hamilton, L8S 4K1, Canada
L. L. Van Dommelen
Affiliation:
Department of Mechanical Engineering, FAMU-FSU College of Engineering, 2525 Pottsdamer Street, Tallahassee, FL 32310-6046, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is an extension of work on separation from a downstream moving wall by Ruban et al. (J. Fluid. Mech., vol. 678, 2011, pp. 124–155) and is in particular concerned with the boundary-layer separation in unsteady two-dimensional laminar supersonic flow. In a frame attached to the wall, the separation is assumed to be provoked by a shock wave impinging upon the boundary layer at a point that moves downstream with a non-dimensional speed which is assumed to be of order 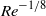where 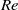is the Reynolds number. In the coordinate system of the shock however, the wall moves upstream. The strength of the shock and its speed are allowed to vary with time on a characteristic time scale that is large compared to 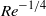. The ‘triple-deck’ model is used to describe the interaction process. The governing equations of the interaction problem can be derived from the Navier–Stokes equations in the limit 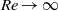. The numerical solutions are obtained using a combination of finite differences along the streamwise direction and Chebyshev collocation along the normal direction in conjunction with Newton linearization. In the present study with the wall moving upstream, the evidence is inconclusive regarding the so-called ‘Moore–Rott–Sears’ criterion being satisfied. Instead it is observed that the pressure rise from its initial value is very slow and that a recirculation region forms, the upstream part of which is wedge-shaped, as also observed in turbulent marginal separation for large values of angle of attack.

JFM classification

Boundary Layers: Boundary layer separation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 413 - 430
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Araki, D. 2006 Boundary-layer separation on moving surface in supersonic flow. PhD thesis, University of Manchester.Google Scholar
2. Blasius, H. 1908 Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Math. Phys. 56, 1–37, Engl. transl. NACA Tech. Mem. 1256.Google Scholar
3. Cebeci, T. 1979 The laminar boundary layer on a circular cylinder impulsively started from rest. J. Comput. Phys. 31, 153.Google Scholar
4. Cebeci, T. 1982 Unsteady separation. In Numerical and Physical Aspects of Aerodynamic Flows (ed. Cebeci, T. ), pp. 265–267. Springer.Google Scholar
5. Cebeci, T. 1986 Unsteady boundary layers with an intelligent numerical scheme. J. Fluid Mech. 129–140.CrossRefGoogle Scholar
6. Christov, C. I. & Tzankov, I. T. 1993 Numerical investigation of the laminar boundary layer flow around an impulsively moved circular cylinder. Comput. Meth. Appl. Mech. 109, 1–15.CrossRefGoogle Scholar
7. Cowley, S. J. 1983 Computer extension and analytic continuation of Blasius expansion for impulsive flow past cylinder. J. Fluid Mech 135, 389–405.CrossRefGoogle Scholar
8. Cowley, S. J., Van Dommelen, L. L. & Lam, S. T. 1990 On the use of Lagrangian variables in description of unsteady boundary-layer separation. Phil. Trans. R. Soc. Lond. A 333, 343–378.Google Scholar
9. Elliott, J. W., Smith, F. T. & Cowley, S. J. 1983 Breakdown of boundary layers (i) on moving surfaces; (ii) in semi-similar flows; (iii) in fully unsteady flow. Geophys. Astrophys. Fluid Dyn. 25, 77–138.Google Scholar
10. Goldstein, S. 1948 On laminar boundary-layer flow near a position of separation. Q. J. Mech. Appl. Maths 1 (1), 43–69.Google Scholar
11. Henkes, R. & Veldman, A. 1987 On the breakdown of the steady and unsteady interacting boundary-layer description. J. Fluid Mech. 179, 513–530.CrossRefGoogle Scholar
12. Ingham, D. B. 1984 Unsteady separation. J. Comput. Phys. 53, 90–99.CrossRefGoogle Scholar
13. Inoue, O. 1981a MRS criterion for flow separation over moving walls. AIAA J. 19, 1108–1111.Google Scholar
14. Inoue, O. 1981b A numerical investigation of flow separation over moving walls. J. Phys. Soc. Japan 50 (3), 1002–1008.Google Scholar
15. Korolev, G., Gajjar, J. S. B. & Ruban, A. I. 2002 Once again on the supersonic flow separation near a corner. J. Fluid. Mech. 463, 173–199.CrossRefGoogle Scholar
16. Koromilas, C. A. & Telionis, D. P. 1980 Unsteady laminar separation: an experimental study. J. Fluid Mech. 97 (2), 347–384.Google Scholar
17. Landau, L. & Lifshitz, E. 1944 Mechanics of Continuous Media. Gostekhizdat.Google Scholar
18. Ludwig, G. R. 1964An experimental investigation of laminar separtion from a moving wall. AIAA Paper 64-6.CrossRefGoogle Scholar
19. Messiter, A. F. 1970 Boundary-layer flow near the trailing edge of a flat plate. SIAM J. Appl. Maths 18 (1), 241–257.Google Scholar
20. Moore, F. K. 1958 On the separation of the unsteady laminar boundary layer. In Boundary Layer research (ed. Görtler, H. ), pp. 431–432. Springer.Google Scholar
21. Neiland, V. Ya 1969 Theory of laminar boundary-layer separation in supersonic flow. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 4, 53–57, English transl. Fluid Dyn. 4 (4), 33–35.Google Scholar
22. Prandtl, L. 1904 Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Verh. III Intl. Math. Kongr., Heidelberg, pp. 484–491. Teubner, Leipzig, 1905, English transl. NACA Tech. Memo. 452.Google Scholar
23. Proudman, I. & Johnson, K. 1962 Boundary-layer growth near a rear stagnation point. J. Fluid Mech. 12, 161–168.Google Scholar
24. Puppo, G. 1990Singularity formation in Prandtl’s equations and a new numerical method. PhD thesis, New York University..Google Scholar
25. Riley, N. & Vasantha, R. 1989 Unsteady high Reynolds number flows. J. Fluid Mech. 205, 243–262.Google Scholar
26. Rizzetta, D. P., Burggraf, O. R. & Jenson, R. 1978 Triple-deck solutions for viscous supersonic and hypersonic flow past corners. J. Fluid Mech. 89 (3), 535–552.Google Scholar
27. Robins, A. J. & Howarth, J. A. 1972 Boundary-layer development at a two-dimensional rear stagnation point. J. Fluid Mech. 56, 161–171.Google Scholar
28. Rott, N. 1956 Unsteady viscous flow in the vicinity of a stagnation point. Q. J. Appl. Maths 13, 444–451.Google Scholar
29. Rott, N. 1964 Theory of time-dependent laminar flows. In Theory of Laminar Flows (ed. Moore, F. ), pp. 395–438. Princeton.Google Scholar
30. Ruban, A. I. 1981 Singular solutions of the boundary layer equations which can be extended continously therough the point of zero surface friction. Fluid Dyn. 16 (6), 835–843.CrossRefGoogle Scholar
31. Ruban, A. I., Araki, D., Yapalparvi, R. & Gajjar, J. S. B. 2011 On unsteady boundary layer separation in supersonic flow. Part 1. Upstream moving separation point. J. Fluid. Mech. 678, 124–155.Google Scholar
32. Scheichl, B. & Kluwick, A. 2007 Turbulent marginal separation and turbulent Goldstein problem. AIAA 45 (1), 20–36.Google Scholar
33. Sears, W. R. 1956 Some recent developments in airfoil theory. J. Aeronaut. Sci 23, 490–499.Google Scholar
34. Sears, W. R. & Telionis, D. P. 1975 Boundary-layer separation in unsteady flow. SIAM J. Appl. Maths 23, 215–235.Google Scholar
35. Shen, S. 1978 Unsteady separation according to the boundary-layer equation. Adv. Appl. Mech. 13, 177.Google Scholar
36. Smith, F. T. 1977 The laminar separation of an incompressible fluid streaming past a smooth surface. Proc. R. Soc. A 356, 443–463.Google Scholar
37. Smith, F. T. & Daniels, P. G. 1981 Removal of Goldstein singularity at separation, in flow past obstacles in wall layers. J. Fluid Mech. 110, 1–37.Google Scholar
38. Stewartson, K. 1958 On Goldstein’s theory of laminar separation. Q. J. Mech. Appl. Maths 11, 399–410.CrossRefGoogle Scholar
39. Stewartson, K. 1969 On the flow near the trailing edge of a flat plate ii. Mathematika 16 (1), 106–121.Google Scholar
40. Stewartson, K. 1970 Is the singularity at separation removable? J. Fluid Mech. 44, 347–364.Google Scholar
41. Stewartson, K., Smith, F. T. & Kaups, K. 1982 Marginal separation. Stud. Appl. Maths 67 (1), 45–61.Google Scholar
42. Stewartson, K. & Williams, P. G. 1969 Self-induced separation. Proc. R. Soc. Lond. A 312, 181–206.Google Scholar
43. Sychev, V. V. 1972 Laminar separation. Izv. Akad. Nauk. SSSR Mekh. Zhidk. Gaza 3, 47–59.Google Scholar
44. Sychev, V. V. 1979 Asymptotic theory of non-stationary separation. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 6, 21–32, English transl. Fluid Dyn. (1980) 14, 829–838.Google Scholar
45. Sychev, V. V., Ruban, A. I., Sychev, V. V. & Korolev, G. L. 1998 Asymptotic Theory of Separated Flows. Cambridge University Press.Google Scholar
46. Telionis, D. & Tsahalis, D. 1974 Unsteady laminar separation over impulsively moved cylinders. Acta Astronaut. 1, 1487–1505.Google Scholar
47. Tsahalis, D. 1977 Laminar boundary-layer separation from an upstream moving wall. AIAA J. 15, 561–566.Google Scholar
48. Van Dommelen, L. L. 1981 Unsteady separation. PhD thesis, Cornell university.Google Scholar
49. Van Dommelen, L. L. & Shen, S. F. 1980 The spontaneous generation of a singularity in a separating boundary layer. J. Comput. Phys. 38, 125–140.Google Scholar
50. Van Dommelen, L. L. & Shen, S. F. 1982 a A bifurcation-free interaction solution for steady separation from a downstream moving wall. AIAA-82-0347.Google Scholar
51. Van Dommelen, L. L. & Shen, S. F. 1982b The genesis of separation. In Symposium on Numerical and Physical Aspects of Aerodynamic Flows (ed. Cebeci, T. ), pp. 293–311. Springer.CrossRefGoogle Scholar
52. Van Dommelen, L. L. & Shen, S. F. 1983a Boundary layer separation singularities for an upstream moving wall. Acta Mechanica 49, 241–254.Google Scholar
53. Van Dommelen, L. L. & Shen, S. F. 1983b An unsteady interactive separation process. AIAA J. 21, 358–362.Google Scholar
54. Van Dommelen, L. L. & Shen, S. F. 1985 The flow at a rear stagnation point is eventually determined by exponentially small values of the velocity. J. Fluid Mech. 157, 1–16.CrossRefGoogle Scholar
55. Vidal, R. J. 1959 Research on rotating stalling axial flow compressor; part III-experiments on laminar separation from a moving wall. Tech. Rep. 59–75. Wright Air Dev. Cent.Google Scholar
56. Wang, K. C. 1979 Unsteady boundary-layer separation. Tech. Rep. MML TR 79-16c. Martin Marietta Laboratory.Google Scholar
57. Williams, J. C. III 1977 Incompressible boundary-layer separation. Annu. Rev. Fluid. Mech. 9, 113–144.Google Scholar