Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T11:23:50.798Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical modelling of supersonic boundary-layer receptivity to solid particulates

Published online by Cambridge University Press:  27 November 2018

Pavel V. Chuvakhov Open the ORCID record for Pavel V. Chuvakhov [Opens in a new window] ,
Alexander V. Fedorov Open the ORCID record for Alexander V. Fedorov [Opens in a new window]  and
Anton O. Obraz
Pavel V. Chuvakhov*
Affiliation:
Moscow Institute of Physics and Technology (MIPT), 9 Institutsky per., Dolgoprudny, Moscow reg., 141701, Russia Central Aerohydrodynamic Institute (TsAGI), 1 Zhukovskogo Str., Zhukovsky, Moscow reg., 140180, Russia
Alexander V. Fedorov*
Affiliation:
Moscow Institute of Physics and Technology (MIPT), 9 Institutsky per., Dolgoprudny, Moscow reg., 141701, Russia
Anton O. Obraz*
Affiliation:
Moscow Institute of Physics and Technology (MIPT), 9 Institutsky per., Dolgoprudny, Moscow reg., 141701, Russia Central Aerohydrodynamic Institute (TsAGI), 1 Zhukovskogo Str., Zhukovsky, Moscow reg., 140180, Russia
*
†Email addresses for correspondence: [email protected], [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Atmospheric particulates may be a major source of boundary-layer instabilities leading to laminar–turbulent transition on aerodynamically smooth bodies flying at supersonic speeds. Particulates penetrating into the boundary-layer flow can excite wavepackets of the first- and/or second-mode instability. The packets grow downstream, reach the threshold amplitude and ultimately break down to turbulent spots. A numerical model is developed to simulate excitation of unstable wavepackets by spherical solid particulates. 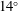As an example, computations are carried out for a $14^{\circ }$ half-angle sharp wedge flying at an altitude of 20 km, Mach number 4 and zero angle of attack. The numerical results agree satisfactorily with the theory developed by Fedorov (J. Fluid Mech., vol. 737, 2013, pp. 105–131). The numerical model opens up an opportunity to investigate receptivity to particulates for practical supersonic and hypersonic configurations such as blunt bodies of revolution.

JFM classification

Boundary Layers: Boundary layer receptivity Boundary Layers: Boundary layer stability Aerodynamics: High-speed flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 949 - 971
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bushnell, D. 1990 Notes on initial disturbance fields for the transition problem. In Instability and Transition (ed. Hussaini, M. Y. & Voigt, R. G.), pp. 217–232. Springer.Google Scholar
Chuvakhov, P. V., Fedorov, A. V. & Obraz, A. O. 2018 Numerical simulation of turbulent spots generated by unstable wave packets in a hypersonic boundary layer. Comput. Fluids 162, 26–38.Google Scholar
Crowe, C. T. 1967 Drag coefficient of particles in a rocket nozzle. AIAA J. 5 (5), 1021–1022.Google Scholar
Egorov, I. V. & Novikov, A. V. 2016 Direct numerical simulation of laminar–turbulent flow over a flat plate at hypersonic flow speeds. Comput. Math. Math. Phys. 56 (6), 1048–1064.Google Scholar
Fedorov, A. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43 (1), 79–95.Google Scholar
Fedorov, A. V. 2013 Receptivity of a supersonic boundary layer to solid particulates. J. Fluid Mech. 737, 105–131.Google Scholar
GAM Guide 1999 Guide to Global Aerosol Models (GAM). AIAA G-065-1999. Available at doi:10.2514/4.473692.001.Google Scholar
Gaponov, S. A. 1980 Effect of Nonparallel Flow on Propagation of Disturbances in a Supersonic Boundary Layer, vol. 2, pp. 26–31. Nauka (in Russian).Google Scholar
Hefner, J. & Bushnell, D.1979 Application of stability theory to laminar flow control. In 12th Fluid and Plasma Dynamics Conference. AIAA paper 1979-1493, available at doi:10.2514/6.1979-1493.Google Scholar
Jewell, J. S. et al. 2017 Effects of shock-tube cleanliness on hypersonic boundary layer transition at high enthalpy. AIAA J. 55 (1), 332–338.Google Scholar
Mack, L. M.1969 Boundary layer stability theory, (Doc./JPL; 900-277, Rev. A), Pasadena, California.Google Scholar
Mack, L. M.1977 Transition and laminar instability. NASA-CP-153203. Jet Propulsion Lab., Pasadena, California.Google Scholar
Nayfeh, A. H. 1980 Stability of three-dimensional boundary layers. AIAA J. 18 (4), 406–416.Google Scholar
Novikov, A., Egorov, I. & Fedorov, A. 2016 Direct numerical simulation of wave packets in hypersonic compression-corner flow. AIAA J. 54 (7), 2034–2050.Google Scholar
Novikov, A. V.2017 Transition induced by a wave train in a supersonic boundary layer over a compression ramp, In 47th AIAA Fluid Dynamics Conference. AIAA paper 2017-4517, available at doi:10.2514/6.2017-4517.Google Scholar
Salemi, L. & Fasel, H. F.2015 Numerical investigation of nonlinear wave-packets in a hypersonic high-enthalpy boundary-layer on a $5^{\circ }$ sharp cone. In 45th AIAA Thermophysics Conference. AIAA paper 2015-2318, available at doi:10.2514/6.2015-2318.Google Scholar
Schneider, S. P. 2008 Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.Google Scholar
Tumin, A. M. & Fedorov, A. V. 1982 On the weakly nonparallel effect on characteristics of flow stability. Uch. Zap. TsAGI 13 (6), 91–96.Google Scholar
Tumin, A. 2007 Three-dimensional spatial normal modes in compressible oundary layers. J. Fluid Mech. 586, 295–322.Google Scholar
Turco, R. P.1992 Upper-atmosphere aerosols: properties and natural cycles. Chapter 3D in: The Atmospheric Effects of Stratospheric Aircraft: A First Program Report, United States, no. 92-19124, pp. 63–91, available at https://ntrs.nasa.gov/search.jsp?R=19920009882.Google Scholar
Zhigulev, V. N. & Tumin, A.M 1987 Onset of Turbulence. Nauka (in Russian).Google Scholar

Chuvakhov et al. supplementary movie

Extension of Fig.7: wall pressure disturbance evolution and isolines dp'w= 5e-7 for the reference case. The particulate collides with the wall at t ≈ 0.009.

Download Chuvakhov et al. supplementary movie(Video)
Video 5.7 MB