Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T11:12:40.332Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical investigation of the wake of an axisymmetric body with appendages

Published online by Cambridge University Press:  03 March 2016

A. Posa  and
E. Balaras
A. Posa
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, 800 22nd Street NW, Washington, DC 20052, USA
E. Balaras*
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, 800 22nd Street NW, Washington, DC 20052, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report wall-resolved large-eddy simulations of an axisymmetric body of revolution with appendages. The geometry is that of the DARPA SUBOFF body at 0 yaw angle and a Reynolds number equal to 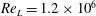$\mathit{Re}_{L}=1.2\times 10^{6}$ (based on the free-stream velocity and the length of the body). The computational grid, composed of approximately 3 billion nodes, is designed to capture all essential flow features, including the turbulent boundary layers on the surface of the body. Our results are in good agreement with measurements available in the literature. It is shown that the wake of the body is affected mainly by the shear layer from the trailing edge of the fins and the turbulent boundary layer growing along the stern, while the influence of the wake of the sail is minimal. In agreement with the reference experiments, a bimodal behaviour for the turbulent stresses is observed in the wake. This is due to the displacement of the maximum of turbulent kinetic energy away from the wall along the surface of the stern, where the boundary layer is subjected to strong adverse pressure gradients. The junction flows, produced by the interaction of the boundary layer with the leading edge of the fins, enhance this bimodal pattern, feeding additional turbulence in the boundary layer and the downstream wake. The evolution of the wake towards self-similarity is also investigated up to nine diameters downstream of the tail. We found the mean flow approaches this condition, while its development is delayed by the wake of the appendages, especially by the flow coming from the tip of the fins. However, the width of the wake and its maximum momentum deficit follow the expected power-law behaviour on the side away from the sail. The second-order statistics, on the other hand, are still far from self-similarity, which is consistent with experimental observations in the literature.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 792 , 10 April 2016 , pp. 470 - 498
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akselvoll, K. & Moin, P. 1996 An efficient method for temporal integration of the Navier–Stokes equations in confined axisymmetric geometries. J. Comput. Phys. 125 (2), 454–463.Google Scholar
Alin, N., Bensow, R. E., Fureby, C., Huuva, T. & Svennberg, U. 2010 Current capabilities of DES and LES for submarines at straight course. J. Ship Res. 54 (3), 184–196.Google Scholar
Aubertine, C. D. & Eaton, J. K. 2005 Turbulence development in a non-equilibrium turbulent boundary layer with mild adverse pressure gradient. J. Fluid Mech. 532, 345–364.Google Scholar
Balaras, E. 2004 Modeling complex boundaries using an external force field on fixed Cartesian grids in large-eddy simulations. Comput. Fluids 33 (3), 375–404.Google Scholar
Balaras, E., Schroeder, S. & Posa, A. 2015 Large-eddy simulations of submarine propellers. J. Ship Res. 59 (4), 227–237.Google Scholar
Beratlis, N., Squires, K. & Balaras, E. 2012 Numerical investigation of Magnus effect on dimpled spheres. J. Turbul. 13, 1–15.Google Scholar
Bhushan, S., Alam, M. F. & Walters, D. K. 2013 Evaluation of hybrid RANS/LES models for prediction of flow around surface combatant and Suboff geometries. Comput. Fluids 88, 834–849.CrossRefGoogle Scholar
Boger, D. A. & Dreyer, J. J. 2006 Prediction of hydrodynamic forces and moments for underwater vehicles using overset grids. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006.Google Scholar
Chase, N. & Carrica, P. M. 2013 Submarine propeller computations and application to self-propulsion of DARPA Suboff. Ocean Engng 60, 68–80.Google Scholar
Chase, N., Michael, T. & Carrica, P. M. 2013 Overset simulation of a submarine and propeller in towed, self-propelled and maneuvering conditions. Intl Shipbuilding Prog. 60 (1–4), 171–205.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Ewing, D., George, W. K., Rogers, M. M. & Moser, R. D. 2007 Two-point similarity in temporally evolving plane wakes. J. Fluid Mech. 577, 287–307.Google Scholar
Galperin, B. 1993 Large Eddy Simulation of Complex Engineering and Geophysical Flows. Cambridge University Press.Google Scholar
Georgiadis, N. J., Rizzetta, D. P. & Fureby, C. 2010 Large-eddy simulation: current capabilities, recommended practices, and future research. AIAA J. 48 (8), 1772–1784.CrossRefGoogle Scholar
Ghosal, S. & Rogers, M. M. 1997 A numerical study of self-similarity in a turbulent plane wake using large-eddy simulation. Phys. Fluids 9 (6), 1729–1739.Google Scholar
Givler, R. C., Gartling, D. K., Engelman, M. S. & Haroutunian, V. 1991 Navier–Stokes simulations of flow past three-dimensional submarine models. Comput. Meth. Appl. Mech. Engng 87 (2–3), 175–200.Google Scholar
Gorski, J. J., Coleman, R. M. & Haussling, H. J.1990 Computation of incompressible flow around the DARPA SUBOFF bodies. Tech. Rep. No. DTRC-90/016, David Taylor Research Center, Bethesda, MD.Google Scholar
Groves, N. C., Huang, T. T. & Chang, M. S.1989 Geometric characteristics of the DARPA SUBOFF models. Tech. Rep. No. DTRC/SHD-1298-01, David Taylor Research Center, Bethesda, MD.Google Scholar
Huang, T., Liu, H. L., Groves, N., Forlini, T., Blanton, J. & Gowing, S. 1994 Measurements of flows over an axisymmetric body with various appendages in a wind tunnel: the DARPA SUBOFF experimental program. In Proceedings of the 19th Symposium on Naval Hydrodynamics, Seoul, Korea, 23–28 August 1992, National Academy Press.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research Report.Google Scholar
Jiménez, J. M., Hultmark, M. & Smits, A. J. 2010a The intermediate wake of a body of revolution at high Reynolds numbers. J. Fluid Mech. 659, 516–539.Google Scholar
Jiménez, J. M., Reynolds, R. T. & Smits, A. J. 2010b The effects of fins on the intermediate wake of a submarine model. ASME J. Fluids Eng. 132 (3), 031102.Google Scholar
Johansson, P. B. V., George, W. K. & Gourlay, M. J. 2003 Equilibrium similarity, effects of initial conditions and local Reynolds number on the axisymmetric wake. Phys. Fluids 15 (3), 603–617.Google Scholar
Lee, J.-H. & Sung, H. J. 2008 Effects of an adverse pressure gradient on a turbulent boundary layer. Intl J. Heat Fluid Flow 29 (3), 568–578.Google Scholar
Meneveau, C., Lund, T. S. & Cabot, W. H. 1996 A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 319, 353–385.Google Scholar
Merz, R. A., Yi, C. H. & Przirembel, C. E. G. 1986 Turbulence intensities in the near-wake of a semielliptical afterbody. AIAA J. 24 (12), 2038–2040.Google Scholar
Monty, J. P., Harun, Z. & Marusic, I. 2011 A parametric study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32 (3), 575–585.Google Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62 (3), 183–200.Google Scholar
Orlanski, I. 1976 A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 21 (3), 251–269.Google Scholar
Patel, V. C., Nakayama, A. & Damian, R. 1974 Measurements in the thick axisymmetric turbulent boundary layer near the tail of a body of revolution. J. Fluid Mech. 63, 345–367.Google Scholar
Phillips, A. B., Turnock, S. R. & Furlong, M. 2010 Influence of turbulence closure models on the vortical flow field around a submarine body undergoing steady drift. J. Mar. Sci. Technol. 15 (3), 201–217.Google Scholar
Posa, A. & Balaras, E. 2014 Model-based near-wall reconstructions for immersed-boundary methods. Theor. Comp. Fluid Dyn. 28 (4), 473–483.Google Scholar
Posa, A., Lippolis, A. & Balaras, E. 2015 Large-eddy simulation of a mixed-flow pump at off-design conditions. ASME J. Fluids Eng. 137 (10), 101302.CrossRefGoogle Scholar
Posa, A., Lippolis, A., Verzicco, R. & Balaras, E. 2011 Large-eddy simulations in mixed-flow pumps using an immersed-boundary method. Comput. Fluids 47 (1), 33–43.Google Scholar
Schlichting, H. 1968 Boundary-Layer Theory. vol. 539. McGraw-Hill.Google Scholar
Skåre, P. E. & Krogstad, P.-Å. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.Google Scholar
Smith, C. E., Beratlis, N., Balaras, E., Squires, K. & Tsunoda, M. 2010 Numerical investigation of the flow over a golf ball in the subcritical and supercritical regimes. Intl J. Heat Fluid Flow 31 (3), 262–273.Google Scholar
Song, S. & Eaton, J. K. 2004 Reynolds number effects on a turbulent boundary layer with separation, reattachment, and recovery. Exp. Fluids 36 (2), 246–258.Google Scholar
Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to $\mathit{Re}_{{\it\theta}}=1410$ . J. Fluid Mech. 187, 61–98.Google Scholar
Spalart, P. R., Deck, S., Shur, M. L., Squires, K. D., Strelets, M. K. & Travin, A. 2006 A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comp. Fluid Dyn. 20 (3), 181–195.Google Scholar
Swarztrauber, P. N. 1974 A direct method for the discrete solution of separable elliptic equations. SIAM J. Numer. Anal. 11 (6), 1136–1150.Google Scholar
Taylor, L. K., Pankajakshan, R., Jiang, M., Sheng, C., Briley, W. R., Whitfield, D. L., Davoudzadeh, F., Boger, D. A., Gibeling, H. J., Gorski, J., Haussling, H., Coleman, R. & Buley, G. 1998 Large-scale simulations for maneuvering submarines and propulsors. In Proceedings of the 29th AIAA Plasmadynamics and Lasers Conference, Albuquerque, NM, USA, 15–18 June 1998.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vanella, M., Posa, A. & Balaras, E. 2014 Adaptive mesh refinement for immersed boundary methods. ASME J. Fluids Engng 136 (4), 040909.CrossRefGoogle Scholar
Van Kan, J. J. I. M. 1986 A second-order accurate pressure-correction scheme for viscous incompressible flow. SIAM J. Sci. Stat. Comput. 7 (3), 870–891.Google Scholar
Vaz, G., Toxopeus, S. & Holmes, S. 2010 Calculation of manoeuvring forces on submarines using two viscous-flow solvers. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010, ASME.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.Google Scholar
Yang, J. & Balaras, E. 2006 An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries. J. Comput. Phys. 215 (1), 12–40.Google Scholar
Zhihua, L., Ying, X. & Chengxu, T. 2011 Numerical simulation and control of horseshoe vortex around an appendage-body junction. J. Fluids Struct. 27 (1), 23–42.Google Scholar
Zhihua, L., Ying, X. & Chengxu, T. 2012 Method to control unsteady force of submarine propeller based on the control of horseshoe vortex. J. Ship Res. 56 (1), 12–22.Google Scholar