Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-29T19:06:15.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of the role of free-stream turbulence in boundary-layer separation

Published online by Cambridge University Press:  21 July 2016

Wolfgang Balzer  and
H. F. Fasel
Wolfgang Balzer*
Affiliation:
Wethersfield, CT, USA
H. F. Fasel
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aerodynamic performance of lifting surfaces operating at low Reynolds number conditions is impaired by laminar separation. In most cases, transition to turbulence occurs in the separated shear layer as a result of a series of strong hydrodynamic instability mechanisms. Although the understanding of these mechanisms has been significantly advanced over the past decades, key questions remain unanswered about the influence of external factors such as free-stream turbulence (FST) and others on transition and separation. The present study is driven by the need for more accurate predictions of separation and transition phenomena in ‘real world’ applications, where elevated levels of FST can play a significant role (e.g. turbomachinery). Numerical investigations have become an integral part in the effort to enhance our understanding of the intricate interactions between separation and transition. Due to the development of advanced numerical methods and the increase in the performance of supercomputers with parallel architecture, it has become feasible for low Reynolds number application (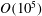$O(10^{5})$) to carry out direct numerical simulations (DNS) such that all relevant spatial and temporal scales are resolved without the use of turbulence modelling. Because the employed high-order accurate DNS are characterized by very low levels of background noise, they lend themselves to transition research where the amplification of small disturbances, sometimes even growing from numerical round-off, can be examined in great detail. When comparing results from DNS and experiment, however, it is beneficial, if not necessary, to increase the background disturbance levels in the DNS to levels that are typical for the experiment. For the current work, a numerical model that emulates a realistic free-stream turbulent environment was adapted and implemented into an existing Navier–Stokes code based on a vorticity–velocity formulation. The role FST plays in the transition process was then investigated for a laminar separation bubble forming on a flat plate. FST was shown to cause the formation of the well-known Klebanoff mode that is represented by streamwise-elongated streaks inside the boundary layer. Increasing the FST levels led to accelerated transition, a reduction in bubble size and better agreement with the experiments. Moreover, the stage of linear disturbance growth due to the inviscid shear-layer instability was found to not be ‘bypassed’.

JFM classification

Wakes/Jets: Separated flows Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent transition
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 289 - 321
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balzer, W.2011 Numerical investigation of the role of free-stream turbulence on boundary-layer separation and separation control. PhD thesis, University of Arizona.CrossRefGoogle Scholar
Boiko, A. V., Grek, G. R., Dogval, A. V. & Kozlov, V. V. 2002 The Origin of Turbulence in Near-wall Flows, 1st edn. Springer.Google Scholar
Brandt, L., Schlatter, P. & Henningson, D. S. 2004 Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 517, 167–198.Google Scholar
Diwan, S. S., Chetan, S. J. & Ramesh, O. N. 2006 On the bursting criterion for laminar separation bubbles. In Laminar-Turbulent Transition, Proceedings of the IUTAM Symposium, pp. 401–407. Springer.CrossRefGoogle Scholar
Dong, Y. & Cumpsty, N. A. 1990 Compressor blade boundary layer. Part 2. Measurements with incident wakes. ASME J. Turbomach. 112, 231–241.CrossRefGoogle Scholar
Dryden, H. L.1936 Air flow in the boundary layer near a plate. NACA Tech. Rep. 562.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flows. Phys. Fluids 18 (4), 487–488.CrossRefGoogle Scholar
Embacher, M.2006 Numerical investigation of secondary absolute instability in laminar separation bubbles. Master’s thesis, University of Arizona.Google Scholar
Fasel, H. F. 1980 Recent developments in the numerical solution of the Navier–Stokes equations and hydrodynamic stability problems. In Computational Fluid Dynamics, pp. 167–279. Hemisphere Publishing Corp.Google Scholar
Fasel, H. F. 2002 Numerical investigation of the interaction of the Klebanoff-mode with a Tollmien–Schlichting wave. J. Fluid Mech. 450, 1–33.CrossRefGoogle Scholar
Fasel, H. F. & Postl, D. 2006 Interaction of separation and transition in boundary layers: direct numerical simulations. In Laminar-Turbulent Transition, Proceedings of the IUTAM Symposium, pp. 71–88. Springer.Google Scholar
Ferziger, J. H. 1998 Numerical Methods for Engineering Application, 2nd edn. Wiley.Google Scholar
Gaster, M. 1966 The structure and behaviour of laminar separation bubbles. In AGARD CP 4, pp. 813–854.Google Scholar
Gatski, T. B. 1991 Review of incompressible fluid flow computations using the vorticity–velocity formulation. Appl. Numer. Meth. 7, 227–239.CrossRefGoogle Scholar
Gault, D. E.1955 An experimental investigation of regions of separated laminar flow. NACA TN 3505.Google Scholar
Ghil, M., Allen, M. R., Dettinger, M. D., Ide, K., Kondrashov, D., Mann, M. E., Robertson, A. W., Saunders, A., Tian, Y., Varadi, F. et al. 2002 Advanced spectral methods for climatic time series. Rev. Geophys. 40 (1), 1‐1–1‐41.CrossRefGoogle Scholar
Häggmark, C.2000 Investigations of disturbances developing in a laminar separation bubble flow. PhD thesis, KTH, Department of Mechanics, Stockholm.Google Scholar
Hernon, D., Walsh, E. J. & McEligot, D. M. 2007 Experimental investigation into the routes to bypass transition and the shear-sheltering phenomenon. J. Fluid Mech. 591, 461–479.Google Scholar
Horton, H. P.1968 Laminar separation in two and three-dimensional incompressible flow. PhD thesis, University of London.Google Scholar
Hourmouziadis, J.2000 Das DFG Verbundvorhaben Instationäre Strömung in Turbomaschinen. Tech. Rep., JT2000-030. DGLR, Deutscher Luft-und Raumfahrtkongress, Leipzig, Germany, September 18–21.Google Scholar
Hunt, J. C. R. & Durbin, P. A. 1999 Perturbed vortical layers and shear sheltering. Fluid Dyn. Res. 24 (6), 375–404.CrossRefGoogle Scholar
Jacobs, R. G. & Durbin, P. A. 1998 Shear sheltering and the continuous spectrum of the Orr–Sommerfeld equation. Phys. Fluids 10 (8), 2006–2011.Google Scholar
Jacobs, R. G. & Durbin, P. A. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.Google Scholar
Jonáš, P., Mazur, O. & Uruba, V. 2000 On the receptivity of the by-pass transition to the length scale of the outer stream turbulence. Eur. J. Mech. (B/Fluids) 19 (5), 707–722.Google Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.Google Scholar
Kendall, J. M.1985 Experimental study of disturbances produced in a pre-transitional laminar boundary layer by weak freestream turbulence. AIAA Paper 1985-1695.CrossRefGoogle Scholar
Kendall, J. M.1990 Boundary layer receptivity to freestream turbulence. AIAA Paper 1990-1504.Google Scholar
Kerschen, E. J. 1991 Linear and nonlinear receptivity to vortical free-stream disturbances. In Boundary Layer Stability and Transition to Turbulence (ed. Reda, D. C., Reed, H. L. & Kobayashi, R.). ASME FED Vol. 114.Google Scholar
Klebanoff, P. 1971 Effect of freestream turbulence on the laminar boundary layer. Bull. Am. Phys. Soc. 10 (11), 1323.Google Scholar
Klebanoff, P. S. & Tidstrom, K. D.1959 Evolution of amplified waves leading to transition in a boundary layer with zero pressure gradient. NASA TN D 195.Google Scholar
Kosorygin, V. S. & Polyakov, N. P. 1990 Laminar boundary layers in turbulent flows. In Laminar-Turbulent Transition, Proceedings of the IUTAM Symposium, pp. 573–578. Springer.CrossRefGoogle Scholar
Kurian, T. & Fransson, J. H. M 2009 Grid-generated turbulence revisited. Fluid Dyn. Res. 41 (2), 021–403.CrossRefGoogle Scholar
Landahl, M. T. 1975 Wave breakdown and turbulence. SIAM J. Appl. Maths 28, 735–756.CrossRefGoogle Scholar
Lardeau, S., Leschziner, M. & Zaki, T. 2012 Large eddy simulation of transitional separated flow over a flat plate and a compressor blade. Flow Turbul. Combust. 88, 19–44.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.CrossRefGoogle Scholar
Levin, O. & Henningson, D. S. 2003 Exponential versus algebraic growth and transition prediction in boundary layer flow. Flow Turbul. Combust. 70, 183–210.Google Scholar
Liu, Y., Zaki, T. A. & Durbin, P. A. 2008a Boundary layer transition by interaction of discrete and continuous modes. J. Fluid Mech. 604, 199–233.Google Scholar
Liu, Y., Zaki, T. A. & Durbin, P. A. 2008b Floquet analysis of secondary instability of boundary layer distorted by Klebanoff streaks and Tollmien–Schlichting waves. Phys. Fluids 20 (12), 124102.CrossRefGoogle Scholar
Luchini, P. 2000 Reynolds number independent instability of the boundary layer over a flat surface. Part 2. Optimal perturbations. J. Fluid Mech. 404, 289–309.Google Scholar
Marxen, O.2005 Numerical studies of physical effects related to the controlled transition process in laminar separation bubbles. PhD thesis, Universität Stuttgart.Google Scholar
Marxen, O., Lang, M. & Rist, U. 2012 Discrete linear local eigenmodes in a separating laminar boundary layer. J. Fluid Mech. 711, 1–26.Google Scholar
Marxen, O., Lang, M. & Rist, U. 2013 Vortex formation and vortex breakup in a laminar separation bubble. J. Fluid Mech. 728, 58–90.Google Scholar
Marxen, O., Lang, M., Rist, U., Levin, O. & Henningson, D. S. 2009 Mechanisms for spatial steady three-dimensional disturbance growth in a non-parallel and separating boundary layer. J. Fluid Mech. 634, 165–189.CrossRefGoogle Scholar
Maucher, U.2000 Numerische Untersuchungen zur Transition in der laminaren Ablöseblase einer Tragflügelgrenzschicht. PhD thesis, Universität Stuttgart.Google Scholar
Mayle, R. E. 1991 The role of laminar-turbulent transition in gas turbine engines. Trans. ASME: J. Turbomach. 113, 509–537.Google Scholar
McAuliffe, B. R. & Yaras, M. I. 2010 Transition mechanisms in separation bubbles under low- and elevated-freestream turbulence. Trans. ASME: J. Turbomach. 132, 011004–011010.Google Scholar
McCullough, G. B. & Gault, D. E.1951 Examples of three representive types of airfoil section stall at low speed. NACA TN 2502.Google Scholar
Meitz, H. L.1996 Numerical investigation of suction in a transitional flat-plate boundary layer. PhD thesis, University of Arizona.Google Scholar
Meitz, H. & Fasel, H. F. 2000 A compact-difference scheme for the Navier–Stokes equations in vorticity–velocity formulation. J. Comput. Phys. 157, 371–403.Google Scholar
Morkovin, M. V. 1969 The many faces of transition. In Viscous Drag Reduction (ed. Wells, C. S.), pp. 1–31. Plenum Press.Google Scholar
Morkovin, M. V.1979 On the question of instabilities upstream of cylindrical bodies. NASA Tech. Rep. CR-3231.Google Scholar
Morkovin, M. V., Reshotko, E. & Herbert, T. 1994 Transition in open flow systmes – a reassessment. Bull. Am. Phys. Soc. 39, 1882.Google Scholar
Ovchinnikov, V., Choudhari, M. M. & Piomelli, U. 2008 Numerical simulations of boundary-layer bypass transition due to high-amplitude free-stream turbulence. J. Fluid Mech. 613, 135–169.Google Scholar
Owen, P. R. & Klanfer, L.1953 On the laminar boundary layer separation from the leading edge of a thin airfoil. Aero. Res. Counc. Tech. Rep. CP 220.Google Scholar
Postl, D.2005 Numerical investigation of laminar separation control using vortex generator jets. PhD thesis, University of Arizona.Google Scholar
Postl, D., Balzer, W. & Fasel, H. F. 2011 Control of laminar separation using pulsed vortex generator jets: direct numerical simulations. J. Fluid Mech. 676, 81–109.Google Scholar
Postl, D. & Fasel, H. F. 2006 Direct numerical simulation of turbulent flow separation from a wall-mounted hump. AIAA J. 44 (2), 263–272.Google Scholar
Rao, V. N., Jefferson-Loveday, R., Tucker, P. G. & Lardeau, S. 2014 Large eddy simulations in turbines: influence of roughness and free-stream turbulence. Flow Turbul. Combust. 92, 543–561.Google Scholar
Rist, U.1998 Zur Instabilität und Transition in laminaren Ablöseblasen. Habilitation, Universität Stuttgart, Aachen: Shaker Verlag, 1999 (Berichte aus der Luft- und Raumfahrttechnik).Google Scholar
Rist, U. & Augustin, K. 2006 Control of laminar separation bubbles using instability waves. AIAA J. 44 (10), 2217–2223.Google Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schubauer, G. B. & Skramstad, H. K.1948 Laminar boundary layer oscillations and transition on a flat plate. NASA Tech. Rep. 909.CrossRefGoogle Scholar
Sharma, O.1998 Impact of Reynolds number on LP turbine performance. In Proceedings of the 1997 Minnowbrook II Workshop on Boundary Layer Transition in Turbomachines. NASA CP-1998-206958: 65-69.Google Scholar
Sohn, K. H. & Reshotko, E.1991 Experimental study of boundary layer transition with elevated freestream turbulence on a heated flat plate. NASA Tech. Rep. CR-187068.Google Scholar
Speziale, C. G. 1987 On the advantages of the vorticity velocity formulation of the equations of fluid-dynamics. J. Comput. Phys. 73, 476–480.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.CrossRefGoogle ScholarPubMed
Volino, R. J. 2002 Separated flow transition under simulated low-pressure turbine airfoil conditions. Part 1. Mean flow and turbulence statistics. Trans. ASME: J. Turbomach. 124, 645–655.Google Scholar
Westin, K. J. A., Boiko, A. V., Klingmann, B. G. B., Kozlov, V. V. & Alfredsson, P. H. 1994 Experiments in a boundary layer subjected to free-stream turbulence. Part 1. Boundary layer structure and receptivity. J. Fluid Mech. 281, 193–218.Google Scholar
Wu, X. & Durbin, P. A. 2001 Evidence of longitudinal vortices evolved from distorted wakes in a turbine passage. J. Fluid Mech. 446, 199–228.Google Scholar
Wu, X., Jacobs, R., Hunt, J. & Durbin, P. A. 1999 Simulation of boundary layer transition induced by periodically passing wakes. J. Fluid Mech. 398, 109–153.Google Scholar
Zaki, T. A., Wissink, J. G., Rodi, W. & Durbin, P. A. 2010 Direct numerical simulation of transition in a compressor cascade: the influence of free-stream turbulence. J. Fluid Mech. 665, 57–98.Google Scholar